计算指数函数的算法

引言

我在上一篇随笔中介绍了计算自然对数的快速算法。现在我们来看看计算指数函数的算法。我们知道，指数函数 e^x 可以展开为泰勒级数：

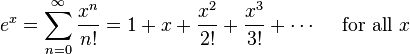
这个级数对全体实数 x 都收敛，并且在 x 接近零时收敛得比较快。

实现该算法的 C# 程序

根据前面所述的 e^x 的泰勒级数展开式，可以写出以下 C# 程序来为 decimal 数据类型添加一个 Exp 扩展方法：

using System;

namespace Skyiv.Extensions
{
  static class DecimalExtensions
  {
    static readonly decimal expmax = 66.542129333754749704054283659m;
    static readonly int[] mask = { 1, 2, 4, 8, 16, 32, 64 };
    static readonly decimal[] exps =
    {
      2.71828182845904523536028747135m, // exp(1)
      7.38905609893065022723042746058m, // exp(2)
      54.5981500331442390781102612029m, // exp(4)
      2980.95798704172827474359209945m, // exp(8)
      8886110.52050787263676302374078m, // exp(16)
      78962960182680.6951609780226351m, // exp(32)
      6235149080811616882909238708.93m  // exp(64)
    };
    
    public static decimal Exp(this decimal x)
    {
      if (x > expmax) throw new OverflowException("overflow");
      if (x < -66) return 0;
      var n = (int)decimal.Round(x);
      if (n > 66) n--;
      decimal z = 1, y = Exponential(x - n);
      for (int m = (n < 0) ? -n : n, i = 0; i < mask.Length; i++)
        if ((m & mask[i]) != 0) z *= exps[i];
      return (n < 0) ? (y / z) : (y * z);
    }
    
    static decimal Exponential(decimal q)
    { // q (almost) in [ -0.5, 0.5 ]
      decimal y = 1, t = q;
      for (var i = 1; t != 0; t *= q / ++i) y += t;
      return y;
    }
  }
}

简要说明如下：

1. 第 7 行的 expmax 的值是 decimal.MaxValue 的自然对数的近似值，用于检测 Exp 方法是否溢出(第 22 行)。
2. 第 20 至 30 行的 Exp 扩展方法就是用来计算指数函数了。
3. 该方法利用 e^x+y = e^xe^y 这个公式，将参数 x 分为整数部分 n 和小数部分 x - n 来计算。
4. 整数部分 n 又分解为 1、2、4、8、16、32、 64 诸数中某些的和，利用事先计算出来的常量来计算。
5. 第 25 行是为了防止将 e^66.5421 分解为 e⁶⁷e^-0.4579，这样在计算 e⁶⁷ 时会溢出。而是分解为 e⁶⁶e^0.5421。
6. 第 32 至 37 行的 Exponential 方法使用泰勒级数来计算 e^x 。它的参数 q 越接近于零就计算得越快。
7. 这个算法还是很快的，第 35 行的 for 循环执行次数不会超过 22 次。

测试程序

下面就是调用 decimal 数据类型的 Exp 扩展方法的测试程序：

using System;
using Skyiv.Extensions;

class Tester
{
  static void Main()
  {
    try
    {
      foreach (var x in new decimal[] {
        -100, -66, -65, -1, 0, 1, 2.5m, 16, 66.5421m, 67 })
        Console.WriteLine("{0,-30}: exp({1})", x.Exp(), x);
    }
    catch (Exception ex) { Console.WriteLine(ex.Message); }
  }
}

运行结果如下所示：

work$ dmcs Tester.cs DecimalExtensions.cs
work$ mono Tester.exe
0                             : exp(-100)
0.0000000000000000000000000000: exp(-66)
0.0000000000000000000000000001: exp(-65)
0.3678794411714423215955237702: exp(-1)
1                             : exp(0)
2.7182818284590452353602874714: exp(1)
12.182493960703473438070175950: exp(2.5)
8886110.520507872636763023741 : exp(16)
79225838488862236701995526357 : exp(66.5421)
overflow

可以看出，在计算 e⁶⁷ 时发现了溢出。这是因为：

• decimal.MaxValue = 79,228,162,514,264,337,593,543,950,335
• e⁶⁷ = 125,236,317,084,221,378,051,352,196,074.4365767534885274 ...

可以看出，e⁶⁷ 已经超过 decimal 的最大值了。

事先计算的常数

在 DecimalExtensions.cs 程序的第 9 至 18 行中的 exps 静态只读数组中存放了 e¹、e²、e⁴、e⁸、e¹⁶、e³² 和 e⁶⁴ 的值。这些值是如何得到的呢？这很简单，Linux 操作系统中有一个高精度计算器 bc 。我们可以先编辑一个如下内容的文本文件 exps_in.txt：

scale=30
e(1)
e(2)
e(4)
e(8)
e(16)
e(32)
e(64)
l(2^96-1)
quit

上面的 e 代表 exp，l 代表 ln，2⁹⁶ - 1 就是 decimal.MaxValue。然后执行以下命令：

work$ bc -l exps_in.txt > exps_out.txt

就可以得出如下内容的输出 exps_out.txt：

2.718281828459045235360287471352
7.389056098930650227230427460575
54.598150033144239078110261202860
2980.957987041728274743592099452888
8886110.520507872636763023740781450350
78962960182680.695160978022635108224219956195
6235149080811616882909238708.928469744831391846235799914388
66.542129333754749704054283659972

稍加整理，就可以用在上述 C# 程序中了：

• 前 7 行就是 e 的各次幂。
• 最后一行就是 decimal.MaxValue 的自然对数。

参考资料

1. Wikipedia: Exponential function
2. Wikipedia: Taylor series
3. Linux man pages: bc - An arbitrary precision calculator language