前言
在上一篇随笔中，我们谈到最小化一个计算中的操作数量不一定会提高它的性能。现在，就让我们来解开为什么会出现这种情况的原因吧。
处理器体系结构
在计算机的处理器中，处理一条指令包括很多操作，可以分为取指(fetch)、译码(decode)、执行(execute)、访存(memory)、写回(write back)和更新程序计数器(PC update)等几个阶段。这些阶段可以在流水线上同时进行，如下图所示：
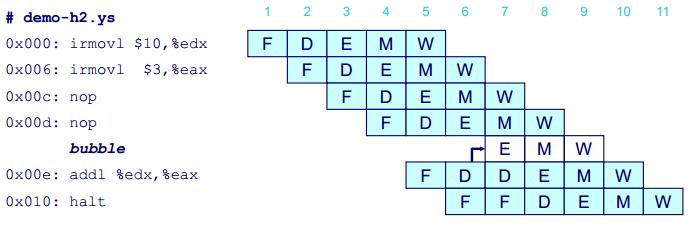
上图中，F、D、E、M 和 W 分别代表上述五个阶段。当然，现代的处理器比这个示例要复杂得多，但是原理是一样的。
- 双精度浮点数乘法: 延迟 5 发射时间 1
- 双精度浮点数加法: 延迟 3 发射时间 1
- 单精度浮点数乘法: 延迟 4 发射时间 1
- 单精度浮点数加法: 延迟 3 发射时间 1
- 整数乘法：延迟 3 发射时间 1
- 整数加法：延迟 1 发射时间 0.33
上面是 Intel Core i7 的一些算术运算的性能。这些时间对于其他处理器来说也是具有代表性的。每个运算都是由两个周期计数值来刻画的：
- 延迟(latency)，表示完成运算所需要的总时间。
- 发射时间(issue time)，表示两个连续的同类型运算之间需要的最小时钟周期数。
我们看到，大多数形式的算术运算的发射时间为 1，意思是说在每个时钟周期，处理器都可以开始一条新的这样的运算。这种很短的发射时间是通过使用流水线实现的。流水线化的功能单元实现为一系列的阶段(stage)，每个阶段完成一部分的运算。例如，一个典型的浮点加法器包含三个阶段(所以有三个周期的延迟)：
- 处理指数值
- 将小数相加
- 对结果进行舍入
算术运算可以连续地通过各个阶段，而不用等待一个操作完成后再开始下一个。只有当要执行的运算是连续的、逻辑上独立的时候，才能利用这种功能。发射时间为 1 的功能单元被称为完全流水线化的(fully pipelined)：每个时钟周期都可以开始一个新的运算。整数加法的发射时间为 0.33，这是因为硬件有三个完全流水线化的能够执行整数加法的功能单元。处理器有能力每个时钟周期执行三个加法。
上述内容来源于《深入理解计算机系统(原书第2版)》。更详细的内容请参阅该书，特别是“第四章 处理器体系结构”和“第五章 优化程序性能”。我们这篇文章讨论的两个算法就来源于该书的“练习题 5.5”和“练习题 5.6”。
分析 poly 函数
下面就是 poly 函数的 C 语言源程序代码：
double poly(double a[], double x)
{
double result = 0, p = 1;
for (int i = 0; i < N; i++, p *= x) result += a[i] * p;
return result;
}
我们在 openSuSE 12.1 操作系统中使用 objdump -d a.out 命令对上一篇随笔中的测试程序进行反汇编，找出其中的 poly 函数的汇编代码如下所示：
0000000000400640 <poly>: 400640: 66 0f 57 d2 xorpd %xmm2,%xmm2 400644: 31 c0 xor %eax,%eax 400646: f2 0f 10 0d 92 01 00 movsd 0x192(%rip),%xmm1 # 4007e0 <_IO_stdin_used+0x10> 40064d: 00 40064e: 66 90 xchg %ax,%ax 400650: f2 0f 10 1c 07 movsd (%rdi,%rax,1),%xmm3 400655: 48 83 c0 08 add $0x8,%rax 400659: 48 3d a8 60 2f 0b cmp $0xb2f60a8,%rax 40065f: f2 0f 59 d9 mulsd %xmm1,%xmm3 400663: f2 0f 59 c8 mulsd %xmm0,%xmm1 400667: f2 0f 58 d3 addsd %xmm3,%xmm2 40066b: 75 e3 jne 400650 <poly+0x10> 40066d: 66 0f 28 c2 movapd %xmm2,%xmm0 400671: c3 retq 400672: 66 66 66 66 66 2e 0f data32 data32 data32 data32 nopw %cs:0x0(%rax,%rax,1) 400679: 1f 84 00 00 00 00 00
可以看出，poly 函数从地址 0x400640 处开始，这与上一篇随笔中测试程序的运行结果相符。我们重点分析循环语句对应的从地址 0x400650 到 0x40066b 之间的代码：
# for (int i = 0; i < N; i++, p *= x) result += a[i] * p; # i in %rax, a in %rdi, x in %xmm0, p in %xmm1, result in %xmm2, z in %xmm3 400650: movsd (%rdi,%rax,1),%xmm3 # z = a[i] 400655: add $0x8,%rax # i++, for 8-byte pointer 400659: cmp $0xb2f60a8,%rax # compare N : i 40065f: mulsd %xmm1,%xmm3 # z *= p 400663: mulsd %xmm0,%xmm1 # p *= x 400667: addsd %xmm3,%xmm2 # result += z 40066b: jne 400650 <poly+0x10> # if !=, goto loop
在 x86-64 体系结构中，%rax, %rdi 是 64-bit 的寄存器，%xmm0, %xmm1, %xmm2, %xmm3 是 128-bit 的浮点寄存器。
在本例中：
- 整型循环变量 i 存放在 %rax 寄存器中。
- 双精度浮点型数组 a 第一个元素的地址存放在 %rdi 寄存器中，注意这个地址是一个 64-bit 的指针，是整数值，而不是浮点值。
- 双精度浮点型输入参数 x 存放在 %xmm0 寄存器中。
- 中间变量 p 存放在 %xmm1 寄存器中。
- 最终结果 result 存放在 %xmm2 寄存器中。
- 此外，GCC C 编译器还使用了一个临时变量 z，存放在 %xmm3 寄存器中。
上述代码中的立即数的含义：
- 0x08: 在 add 指令中使用，使 %rax 加上字长 8-byte，达到 i++ 的目的。
- 0xb2f60a8: 在 cmp 指令中使用，它等于 187654312，除以字长 8-byte 就是 23456789，即 N 的值。
- 0x400650: 在 jne 指令中使用，指明跳转的目的地。
我们可以看到，这里限制性能的计算是反复地计算表达式 p *= x。这需要一个双精度浮点数乘法(5个时钟周期)，并且直到前一次迭代完成，下一次迭代的计算才能开始。两次连续的迭代之间，还要计算表达式 z *= p， 这需要一个双精度浮点乘法(5个时钟周期)，以及计算表达式 result += z， 这需要一个双精度浮点加法(3个时钟周期)。这三个涉及浮点数运算的表达式的计算都可以在流水线上同时地进行。最终，完成一次循环迭代需要5个时钟周期。
在这个汇编程序中，C 语言编译器充分利用了处理器提供的指令级并行(instruction-level parallelism)能力，同时执行多条指令，以达到优化程序性能的目的。
分析 polyh 函数
这下面就是 polyh 函数的 C 语言源程序代码：
double polyh(double a[], double x)
{
double result = 0;
for (int i = N - 1; i >= 0; i--) result = result * x + a[i];
return result;
}
对应的汇编语言代码如下所示：
0000000000400680 <polyh>: 400680: 66 0f 57 c9 xorpd %xmm1,%xmm1 400684: 31 c0 xor %eax,%eax 400686: 66 2e 0f 1f 84 00 00 nopw %cs:0x0(%rax,%rax,1) 40068d: 00 00 00 400690: f2 0f 59 c8 mulsd %xmm0,%xmm1 400694: f2 0f 58 8c 07 a0 60 addsd 0xb2f60a0(%rdi,%rax,1),%xmm1 40069b: 2f 0b 40069d: 48 83 e8 08 sub $0x8,%rax 4006a1: 48 3d 58 9f d0 f4 cmp $0xfffffffff4d09f58,%rax 4006a7: 75 e7 jne 400690 <polyh+0x10> 4006a9: 66 0f 28 c1 movapd %xmm1,%xmm0 4006ad: c3 retq 4006ae: 66 90 xchg %ax,%ax
同样可以看出，polyh 函数从地址 0x400680 处开始，也与上一篇随笔中测试程序的运行结果相符。需要重点分析的循环语句位于地址 0x400690 到 0x4006a7 之间：
# for (int i = N - 1; i >= 0; i--) result = result * x + a[i]; # i in %rax, a in %rdi, x in %xmm0, result in %xmm1 400690: mulsd %xmm0,%xmm1 # result *= x 400694: addsd 0xb2f60a0(%rdi,%rax,1),%xmm1 # result += a[i] 40069d: sub $0x8,%rax # i--, for 8-byte pointer 4006a1: cmp $0xfffffffff4d09f58,%rax # compare 0 : i 4006a7: jne 400690 <polyh+0x10> # if !=, goto loop
上述程序中几个立即数的含义:
- 0x8: 在 sub 指令中使用，从 %rax 中减去字长 8-byte，达到 i-- 的目的。
- 0xb2f60a0: 在 addsd 指令中使用，它等于 187654304，除以字长 8-byte 就是 23456788，即 N - 1 的值。
- 0xfffffffff4d09f58: 在 cmp 指令中使用，它加上 0xb2f60a0 就是 0xfffffffffffffff8，再加上 0x8 就等于 0。
- 0x400690: 在 jne 指令中使用，指明该指令跳转的目的地。
类似地：
- 整型循环变量 i 存放在 %rax 寄存器中。
- 双精度浮点型数组 a 第一个元素的地址存放在 %rdi 寄存器中。
- 双精度浮点型输入参数 x 存放在 %xmm0 寄存器中。
- 最终结果 result 存放在 %xmm1 寄存器中。
我们可以看到，这里限制性能的计算是求表达式 result *= x 和 result += a[i] 的值。从来自上一次迭代的 result 的值开始，我们必须先把它乘以 x (需要 5 个时钟周期)，然后把它加上 a[i] (需要 3 个时钟周期)，然后得到本次迭代的值。因此，完成一次循环迭代需要 8 个时钟周期，比原始的算法需要的 5 个时钟周期更慢。注意，由于后一个表达式 result += a[i] 的计算需要前一个表达式 result *= x 的值，所以这两个表达式的计算不能在流水线上同时进行。这里由于数据相关(data dependency)，无法利用处理器提供的指令级并行能力来优化程序性能。
结论
优化程序性能不是一件简单的事，必须对计算机系统的核心概念有所了解。现代计算机用复杂的技术来处理机器级程序，并行地执行许多指令，执行顺序还可能不同于它们在程序中现出的顺序。程序员必须理解这些处理器是如何工作的，从而调整他们的程序以获得最大的速度。强烈推荐《深入理解计算机系统(原书第2版)》这本书。
