Timus 1016. A Cube on the Walk

Timus 1016. A Cube on the Walk 要求给出一个立方体在国际象棋棋盘上的最短路径。

---

1016. A Cube on the Walk

Time Limit: 2.0 second
Memory Limit: 16 MB

A cube placed on some square of a usual chessboard. A cube completely covers one square of the chessboard but not anything more, i.e. size of cube’s edge is equal to the size of square’s edge. The integer number N (0 ≤ N ≤ 1000) is written on the each side of the cube. However it does not imply that the same number is written on all sides. On the different sides there are might be different numbers. One can move a cube to the next square by rotating it around the common edge of the cube and the square. During this motion the sum of the numbers on the bottom of the cube is calculated (each number is added as much times as it appeared at the bottom of the cube). Your task is to find the route between two given squares with the minimal sum of numbers on the bottom side. The numbers on the bottom at the beginning and at the end of walk are also counted. The start and the end positions are different.

Input

The only line of the input contains the necessary data set (only spaces used as delimiters). First, the start position is given, and then the end position. Each position is composed from the character (from ‘a’ to ‘h’ inclusively, it defines the number of the column on the chessboard) and the digit (from ‘1’ to ‘8’ inclusively, it defines the number of the row). That positions are followed by 6 numbers which are currently written on the forward, backward, top, right, bottom and left sides of the cube correspondingly.

Output

The only line of the output must contain the minimal sum followed by the optimal route (one of possible routes with minimal sum). The route must be represented by the sequence of cube’s positions during the walk. It begins with the start square and ends with the finish square. All square positions on the chessboard should be given in the same format as in input. Use spaces as delimiters.

Sample

input	output
e2 e3 0 8 1 2 1 1	5 e2 d2 d1 e1 e2 e3

Problem Source: Ural State University Internal Contest '99 #2

---

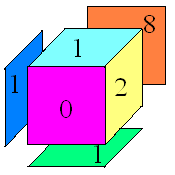
这道题目是说，一个立方体放在国际象棋棋盘的一个格子上，该立方体每一面都和棋盘的格子一样大。该立方体每一面都标有一个非负整数。你可以在棋盘上滚动该立方体，在这期间计算立方体底面数字的和。你的任务是找出一条从给定的起点到终点的路径，使得前面所说的和最小。

输入只有一行，使用空格作为分隔符。首先是棋盘上的起点和终点的坐标，然后是立方体上的六个整数，按顺序为：前、后、顶、右、底、左面。举例如下： e2 e3 0 8 1 2 1 1 。

输出也只有一行，使用空格作为分隔符。首先是所求的最小的和。然后依次给出所求的路径的坐标。举例如下：5 e2 d2 d1 e1 e2 e3 。这个路径共六步，其长度为：1 + 1 + 0 + 1 + 1 + 1 = 5 。

上面的输入和输出的例子是题目中给出的。其实同一个输入可能不止一条最短路径。例如使用我的程序得到的输出如下：5 e2 e1 f1 f2 e2 e3 。这个路径也是六步，其长度为： 1 + 0 + 2 + 1 + 0 + 1 = 5 。

好了，我们还是来看程序吧。

第 43 到 116 行的 Cube 类代表立方体。

第 45 到 47 行的 X、Y、Z 表示立方体绕三个坐标轴旋转，如图所示。

第 48 行的 DCube 数组的四个元素表示立方体在棋盘上向“左、上、右、下”滚动。与此相对应的第 53 行的 DSize 数组的四个元素表示与棋盘当前格子相邻的“左、上、右、下”格子。

第 49 行的 Levels 数组共有 24 个元素，表示同一立方体的 24 种不同的状态，是通过调用第 106 到 115 行的 GetLevels 方法得到的。类似地，“Timus 1015. Test the Difference! 要求将赌场中的骰子分类” 中每种骰子也对应 24 种不同的状态。

程序的主体是第 123 到 130 行的 Run 方法。该方法的第 126 行调用 Read 方法获取输入。然后在第 127 行调用 Dijkstra 方法寻找最短路径。最后在第 128 到 129 行输出结果。

第 142 到 164 行的 Dijkstra 方法是程序的关键部分。第 144 行的三维数组 prev 用来记录立方体的路径，由 24 层的 8x8 棋盘构成。第 145 行的优先队列 q 的元素类型是 Rectangle，其构造函数的参数是 new Comparer() 。Comparer 类在第 11 到 17 行定义，用于逆序比较 Rectangle 的 Width 属性，该 Width 属性表示所求的最小的和。第 146 行将立方体的初始位置压入优先队列。第 147 行的三维数组 dist 大小是 8x8x24，用来记录路径长度，其元素被初始化为无穷大。第 150 到 162 行的循环使用 Dijkstra 算法寻找最短路径。最后在第 163 行调用 GetPath 方法返回找到的最短路径。

  1 using System;
  2 using System.IO;
  3 using System.Drawing;
  4 using System.Collections.Generic;
  5 
  6 namespace Skyiv.Ben.Timus
  7 {
  8   // http://acm.timus.ru/problem.aspx?space=1&num=1016
  9   sealed class T1016
 10   {
 11     sealed class Comparer : IComparer<Rectangle>
 12     {
 13       public int Compare(Rectangle x, Rectangle y)
 14       {
 15         return (x.Width == y.Width) ? 0 : ((x.Width < y.Width) ? 1 : -1);
 16       }
 17     }
 18   
 19     sealed class PriorityQueue<T>
 20     {
 21       List<T> queue = new List<T>();
 22       IComparer<T> comparer;
 23       
 24       public PriorityQueue(IComparer<T> comparer)
 25       {
 26         this.comparer = comparer;
 27       }
 28       
 29       public void Push(T v)
 30       {
 31         int i = queue.BinarySearch(v, comparer);
 32         queue.Insert((i < 0) ? ~i : i, v);
 33       }
 34       
 35       public T Pop()
 36       {
 37         T v = queue[queue.Count - 1];
 38         queue.RemoveAt(queue.Count - 1);
 39         return v;
 40       }
 41     }
 42     
 43     sealed class Cube : IEquatable<Cube>, IComparable<Cube>
 44     {
 45       static readonly Cube X = new Cube(0, 1, 5, 2, 3, 4);
 46       static readonly Cube Y = new Cube(2, 4, 1, 3, 0, 5);
 47       static readonly Cube Z = new Cube(3, 5, 2, 1, 4, 0);
 48       static readonly Cube[] DCube = { X, Y, X * X * X, Y * Y * Y };
 49       static readonly Cube[] Levels = GetLevels();
 50       static readonly int idxBottom = 4;
 51       public static readonly int Size = 8; // for chessboard: 8x8
 52       public static readonly int Level = Levels.Length; // 24
 53       public static readonly Size[] DSize = { new Size(-1,0), new Size(0,1), new Size(1,0), new Size(0,-1) };
 54       
 55       int[] v = new int[6]; // Forward, Backward, Top, Right, Bottom, Left
 56       public int Bottom { get { return v[idxBottom]; } }
 57       
 58       Cube()
 59       {
 60         for (int i = 0; i < v.Length; i++) v[i] = i;
 61       }
 62       
 63       public Cube(params int[] v)
 64       {
 65         for (int i = 0; i < v.Length; i++) this.v[i] = v[i];
 66       }
 67       
 68       public bool Equals(Cube other)
 69       {
 70         return CompareTo(other) == 0;
 71       }
 72       
 73       public int CompareTo(Cube other)
 74       {
 75         int i = 0;
 76         while (i < v.Length && v[i] == other.v[i]) i++;
 77         return (i == v.Length) ? 0 : ((v[i] < other.v[i]) ? -1 : 1);
 78       }
 79       
 80       public static Cube operator*(Cube x, Cube y)
 81       {
 82         Cube z = new Cube();
 83         for (int i = 0; i < z.v.Length; i++) z.v[y.v[i]] = x.v[i];
 84         return z;
 85       }
 86       
 87       public static Cube operator/(Cube x, Cube y)
 88       {
 89         Cube z = new Cube();
 90         for (int i = 0; i < z.v.Length; i++) z.v[i] = y.v[x.v[i]];
 91         return z;
 92       }
 93 
 94       public static int GetLevel(int level, int n)
 95       {
 96         return Array.BinarySearch(Levels, Levels[level] / DCube[n]);
 97       }
 98       
 99       public int GetBottom(int level)
       {
         int i = 0;
         while (Levels[level].v[i] != idxBottom) i++;
         return v[i];
       }
       
       static Cube[] GetLevels()
       {
         List<Cube> list = new List<Cube>();
         Cube v, x = new Cube(), y = new Cube(), z = new Cube();
         for (int i = 0; i < 4; i++, x *= X)
           for (int j = 0; j < 4; j++, y *= Y)
             for (int n, k = 0; k < 4; k++, z *= Z)
               if ((n = list.BinarySearch(v = x * y * z)) < 0) list.Insert(~n, v);
         return list.ToArray();
       }
     }
     
     static void Main()
     {
       new T1016().Run(Console.In, Console.Out);
     }
     
     void Run(TextReader reader, TextWriter writer)
     {
       Point start, end;
       Cube cube = Read(reader, out start, out end);
       Point[] path = Dijkstra(cube, start, end);
       writer.Write(path[0].X);
       for (int i = 1; i < path.Length; i++) writer.Write(PutPosition(path[i]));
     }
     
     Cube Read(TextReader reader, out Point start, out Point end)
     {
       string[] ss = reader.ReadLine().Split();
       start = GetPosition(ss[0]);
       end = GetPosition(ss[1]);
       int[] v = new int[ss.Length - 2];
       for (int i = 0; i < v.Length; i++) v[i] = int.Parse(ss[i + 2]);
       return new Cube(v);
     }
     
     Point[] Dijkstra(Cube cube, Point start, Point end)
     {
       Rectangle[,,] prev = new Rectangle[Cube.Size, Cube.Size, Cube.Level];
       PriorityQueue<Rectangle> q = new PriorityQueue<Rectangle>(new Comparer());
       q.Push(new Rectangle(start.X, start.Y, cube.Bottom, 0));
       int[,,] dist = GetDistance();
       dist[start.X, start.Y, 0] = cube.Bottom;
       Rectangle v;
       while ((v = q.Pop()).Location != end)
         if (v.Width <= dist[v.X, v.Y, v.Height])
           for (int i = 0; i < Cube.DSize.Length; i++)
           {
             Point pt = v.Location + Cube.DSize[i];
             if (pt.X < 0 || pt.Y < 0 || pt.X >= Cube.Size || pt.Y >= Cube.Size) continue;
             int height = Cube.GetLevel(v.Height, i);
             int width = v.Width + cube.GetBottom(height);
             if (dist[pt.X, pt.Y, height] <= width) continue;
             dist[pt.X, pt.Y, height] = width;
             prev[pt.X, pt.Y, height] = v;
             q.Push(new Rectangle(pt.X, pt.Y, width, height));
           }
       return GetPath(prev, start, end, v.Height, dist[end.X, end.Y, v.Height]);
     }
     
     Point[] GetPath(Rectangle[,,] prev, Point start, Point end, int id, int len)
     {
       Stack<Point> path = new Stack<Point>();
       for (Rectangle v = new Rectangle(end.X, end.Y, 0, id);
         v.Location != start || v.Height != 0;
         v = prev[v.X, v.Y, v.Height]) path.Push(v.Location);
       path.Push(start);
       path.Push(new Point(len, 0));
       return path.ToArray();
     }
     
     int[,,] GetDistance()
     {
       int[,,] dist = new int[Cube.Size, Cube.Size, Cube.Level];
       for (int i = 0; i < dist.GetLength(0); i++)
         for (int j = 0; j < dist.GetLength(1); j++)
           for (int k = 0; k < dist.GetLength(2); k++)
             dist[i, j, k] = int.MaxValue; // infinity
       return dist;
     }
     
     Point GetPosition(string s)
     {
       return new Point(s[0] - 'a', s[1] - '1');
     }
     
     string PutPosition(Point pt)
     {
       return string.Format(" {0}{1}", (char)(pt.X + 'a'), pt.Y + 1);
     }
   }
 }

---

返回目录