1081. Binary Lexicographic Sequence
Time Limit: 0.5 second
Memory Limit: 16 MB
Input
Output
Sample
| input | output |
|---|---|
|
3 1 |
000 |
Problem Source: Winter Mathematical Festival Varna '2001 Informatics Tournament
解答如下：
2 using System.IO;
3
4 namespace Skyiv.Ben.Timus
5 {
6 // http://acm.timus.ru/problem.aspx?space=1&num=1081
7 class T1081
8 {
9 static void Main()
10 {
11 new T1081().Run(Console.In, Console.Out);
12 }
13
14 void Run(TextReader reader, TextWriter writer)
15 {
16 string[] ss = reader.ReadLine().Split();
17 short[] bs = GetBinarys(int.Parse(ss[0]), int.Parse(ss[1]));
18 if (bs == null) writer.Write(-1);
19 else for (int i = bs.Length - 1; i >= 0; i--) writer.Write(bs[i]);
20 }
21
22 short[] GetBinarys(int n, int k)
23 {
24 short[] bs = new short[n];
25 int[] fib = GetFibonacci(n);
26 for (int i = n + 2; k > 1; k -= fib[i])
27 {
28 i = Seek(fib, i - 2, k);
29 if (i >= n) return null;
30 bs[i] = 1;
31 }
32 return bs;
33 }
34
35 int[] GetFibonacci(int n)
36 {
37 int[] fib = new int[n + 1];
38 fib[0] = 1;
39 fib[1] = 2;
40 for (int i = 2; i <= n; i++) fib[i] = fib[i - 1] + fib[i - 2];
41 return fib;
42 }
43
44 int Seek(int[] fib, int m, int k)
45 {
46 for (int i = m; i >= 0; i--) if (fib[i] < k) return i;
47 return -1;
48 }
49 }
50 }
这道题要求给出第 K (0 < K < 109) 个 N (0 < N < 44) 位二进制数，该二进制数不得有相邻的“1”。由于时间限制是 0.5 秒，肯定不能使用蛮力搜索从 1 列举到 K。
我们以 N = 5 来分析看看有没有什么规律。如左图所示，我们发现该二进制数最左边的“1”开始在第几个数之后出现是很规律的，如下所示(左图中红色粗框中的数)：
1, 2, 3, 5, 8, 13, ...
也就是说，后项等于前二项之和。这不正是扔掉第一项后的斐波那契 ( Fibonacci ) 数列吗？
于是，程序在第 35 到 42 行的 GetFibonacci() 方法中计算出该数列。然后在第 22 到 33 的 GetBinarys() 方法中计算出第 K 个满足条件的二进制数。该方法在第 26 到 31 行的循环中从高位到低位设定“1”(如左图中红色细框所示)。
请注意，左图中两块阴影部分的内容是相同的，都代表了 N = 3 的情况。也就是说，N = 5 的最低三位是在重复 N = 3 的情况。并且由于该二进制数不得有相邻的“1”，所以在程序第 28 行使用 i - 2 而不是 i - 1 作为第 2 个参数调用 Seek() 方法，然后在第 30 行将该二进制数的第 i 位设为“1”。最后在第 26 行 k -= fib[i]，以进入下一轮循环，直到 k 降低到 1 而结束循环。
本程序的算法应该是最优的，其时间复杂度为 O(N)。本程序的运行时间是 0.078 秒，其 C++ 版本程序的运行时间是 0.001 秒。
我们知道，斐波那契 ( Fibonacci ) 数列定义如下：
F1 = 1, F2 = 1, Fn = Fn-1 + Fn-2 (n > 2)
她的前几项如下：
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ...
她的通项公式如下：
Fn = ( (1+ √5) / 2 )n / √5 - ( (1- √5) / 2 )n / √5 ≈ O(1.618n)
由于程序中的 fib 数组的下标是从 0 开始，且扔掉了斐波那契 ( Fibonacci ) 数列的第一项，所以 fib[n] = Fn+2。
从上图中可以看出，N 位没有相邻的“1”的二进制数共有 fib[N] 个，也就是 FN+2 ≈ O(1.618N+2) 个。
所以，如果使用蛮力搜索从 1 列举到 K，其时间复杂度约为 O(1.618N+2)。
在本题中，要求给出第 K (0 < K < 109) 个 N (0 < N < 44) 位没有相邻的“1”的二进制数。实际上 fib[43] = F45 = 1,134,903,170 ≈ 109。所以 K 和 N 的大小是匹配的。
我用 C++ 语言写了一个蛮力搜索从 1 列举到 K 的程序，如下：
2 #include <iostream>
3
4 const int N_MAX = 43;
5 __int64 mask[N_MAX + 1];
6
7 void init(int n)
8 {
9 mask[0] = 1;
10 for (int i = 1; i <= n; i++) mask[i] = mask[i - 1] << 1;
11 }
12
13 int valid(__int64 bin, int n)
14 {
15 while (n >= 0 && (bin & mask[n]) == 0) n--;
16 while (n > 0)
17 {
18 if (bin & mask[--n]) return 0;
19 while (n >= 0 && (bin & mask[n]) == 0) n--;
20 }
21 return 1;
22 }
23
24 __int64 getBinary(int n, int k)
25 {
26 __int64 bin = 0;
27 for ( ; k > 0; bin++)
28 {
29 if (bin >= mask[n]) return -1;
30 if (valid(bin, n - 1)) k--;
31 }
32 return bin - 1;
33 }
34
35 int main()
36 {
37 int n, k;
38 std::cin >> n >> k;
39 init(n);
40 __int64 bin = getBinary(n, k);
41 if (bin < 0) std::cout << -1;
42 else for (int i = n - 1; i >= 0; i--) std::cout << ((bin & mask[i]) ? 1 : 0);
43 }
将该程序提交到 Timus Online Judge，果然超时：
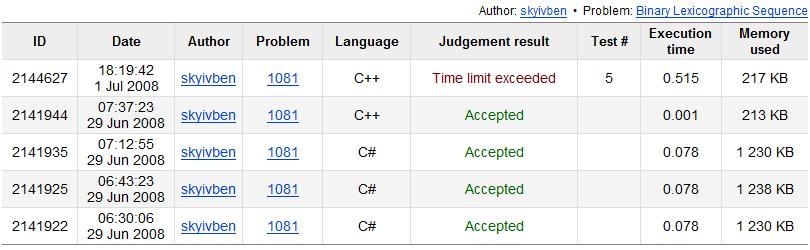
上图中，ID 为 2144627 的记录(运行到 0.515 秒后因为超时而被终止)就是蛮力搜索程序的运行结果，而 ID 为 2141944 的记录(运行时间为 0.001 秒)就是将前面 C# 程序翻译为 C++ 程序的运行结果。
