noi前第十八场 题解

A. 林海的密码#

难点主要就是如何构造加法操作。

一个点数 $2 \log n$，边数 $5 \log n$ 的做法是这样的。

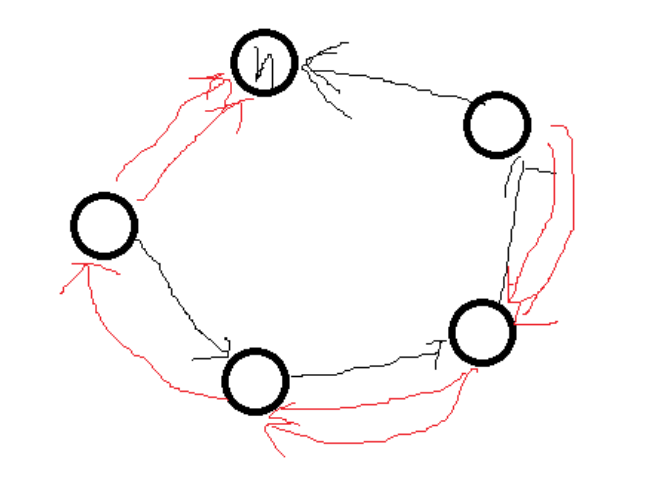
像这样构造一个双向的环，显然一个内向生成树为断掉红边的后缀、黑边的前缀。
发现这样每次只能使贡献 $*2$ 或者不变，所以问题就是用若干个连续的 $2$ 的次幂把 $c$ 拼凑出来。
容易发现先从小到大倍增，后从大到小倍增就好了。

另一个点数 $\log n$，边数 $3 \log n$ 的做法是这样的。

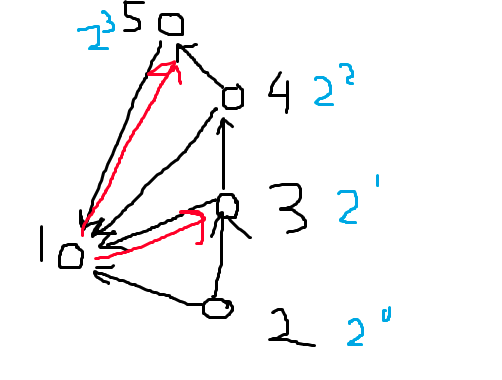
考虑保留了哪条红边，那么红边以下的点均有 $2$ 种选择，红边以上的点选择唯一。
所以可以根据 $c$ 在二进制下哪些位为 $1$ 选出红边。
 

B. 皮卡丘#

把操作离线下来，建出树来。
在树上打个标记模拟一下就好了。
 

C. 我永远喜欢#

考虑序列上的问题，可以首先对同类的点进行划分。
对于同类的 $n$ 个点划分为 $i$ 个连续段造成的贡献和，有 $f_{n,i}=[x^n](e^x-1)^i$，这个式子推一推就发现是卷积式。
然而直接合并会出现连接到一起的情况，所以二项式反演容斥一下。
分治 FFT 把这样的 EGF 卷积到一起即可。

对于环上的情况，考虑钦定第一个元素为第一类，并且最后一个元素不为第一类。
计算的方式就是给第一个元素对应的 EGF 左移若干位，表示钦定其中若干个不参与排列。
考虑这样每个方案被计算的次数为 第一个元素所在的连续段数/循环节数，而我们想要的计算次数为 循环节长度 次。
所以修改一下第一个元素的 EGF，把连续段数除掉，再乘上一个序列总长即可。