模拟7 题解

A. 方程的解

a，b均为正整数，exgcd求出x最小和最大的解。

作差后除公差再加一，就是方程的解的数量。

对于a，b，c中存在0或负数的情况，疯狂加特判。

 

B. visit

共走t步，要求到达坐标$(n,m)$。

即总共向上走了n步，向右走了m步。

设u为向上走步数，d为向下走步数，l为向左，r为向右。

则有：

$u-d=n$

$r-l=m$

$u+d+l+r=t$

如果t-n-m为奇数，则不可能存在一种方案用t步到达$(n,m)$，

因为无法将剩余的步数均等地分配给向上和向下，向左和向右。

枚举其中任意一个，即可利用组合数求解，将答案求和。

$ans=\sum \limits_{i=n,2|(i-n)}^{t-m} \binom{t}{i} \binom{i}{\frac{i-n}{2}} \binom{t-i}{\frac{t-i-m}{2}}$    

本题 膜 数不保证是质数，但保证是不同质数的乘积。

对每个质因子使用lucas定理求出结果，将结果用crt合并就是最终的答案。

题中没保证n，m是正数，但n，m为负的情况与均为正数等价，注意转换。

 

C. 光

60分算法：

暴力模拟。

按照题面中说的做，遇到未经过的点时，$ans++$。

对每一个方格，来自每一个方向的情况，

开一个bool数组判断是否经过过。

当遇到已经经过的，即已经有循环，break退出即可。

 

考虑如何优化暴力。

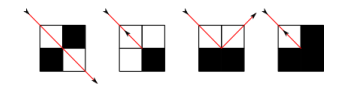
设这几种情况分别为1，2，3，4。

首先通过手玩，发现一些性质：

性质1：

当且仅当光线遇到情况2，4，每个方格会被来自相对两个方向的光线经过。

如果不遇到情况2，4，每个方格仅会被一个方向的光线经过。

证明：

设（x，y）为四个格子交界处的格点坐标。

考虑向每个方向移动 对x+y的贡献，

x y均+1或-1，x+y的奇偶性不变。

x y分别+1 -1，x+y的奇偶性不变。

于是全程中x+y的奇偶性不会改变。

所以每个方格周围只有两个格点可能被经过，

也就最多被来自两个相对方向的光线经过。

性质2：

光线在无转向的运动过程中，

x+y不变，或x-y不变。

性质3：

由于障碍只有k个，边界的数量只与n，m线性相关。

障碍物的每个方向至多反弹一次。

光线的总反弹次数是 $n+m+k$ 级别的。

 

根据性质2，我们对每个x+y，x-y都开一个set（或经过排序的vector），

将每个障碍物（包括边界）插入对应的set，可以通过二分查找前驱后继，

在一次转向后可快速找到下次转向的位置。

光线的总反弹次数大概就是 $n+m+k$ 级别的，所以复杂度是可以接受的。

 

当与起点方向方向相同时走到起点时，可以跳出循环。

记录是否遇到过情况2，4，

如果存在，将ans/2。

复杂度$O(NlogN)$