bzoj2839 集合计数 组合计数 容斥原理|题解
集合计数
题目描述
一个有N个元素的集合有2^N个不同子集（包含空集），现在要在这2^N个集合中取出若干集合（至少一个），使得它们的交集的元素个数为K，求取法的方案数，答案模1000000007。（是质数喔~）
输入格式
一行两个整数N,K
输出格式
一行为答案。
样例
样例输入
3 2样例输出
6数据范围与提示
样例说明
假设原集合为{A,B,C}
则满足条件的方案为：{AB,ABC},{AC,ABC},{BC,ABC},{AB},{AC},{BC}
数据说明
对于100%的数据，1≤N≤1000000；0≤K≤N；
题解
看到这个题我们很自然的想到答案是
$\binom{n}{k}*f(n-k)$
其中f（i）表示i个元素的2i个集合中，选出任意多集合使交集为空的方案数，但是一个集合都不选是不合法的
一个暴力算法
显然f（0）=1
设g（i，j）表示从i个元素的集合中，选出任意多集合使交集为k个的方案数
$g(i，j)=\binom{i}{j}*f(i-j)$
对于i>1 $f(i)=2^{2^i}-1-\sum\limits_{j=1}^{i}g(i,j)$
注意不能一个集合都不选，但可以选择集合中没有任何元素的集合来组成一个对集合的集合，这涉及到-1的位置
复杂度O（n2） 期望得分70
正解 容斥原理
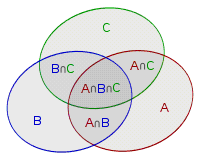
$f(n)=\sum\limits_{i=0}^{n}*(-1)^i*\binom{n}{i}*(2^{2^{n-i}}-1)$
集合A B C表示交集中含有 a，b，c的集合取法
C（n，i）表示从n个形如A B C的集合中取出i个，算出有多少种取法
这i个集合的交集则表示同时含有这i个元素
后一项则表示其他集合任意选取，但不能一个都不选的方案数
偶加奇减，则得到全集减去这几个集合的并集，得到f（i）
1 #include<iostream>
2 #include<cstdio>
3 #define ll long long
4 using namespace std;
5 const int mod=1e9+7;
6 int n,k;
7 ll js[1000010],jsinv[1000010];
8 ll qpow(ll base,int y,int mo)
9 {
10 ll ans=1;
11 while(y)
12 {
13 if(y&1) ans=ans*base%mo;
14 base=base*base%mo;
15 y>>=1;
16 }
17 return ans;
18 }
19 void init()
20 {
21 js[0]=1;
22 for(int i=1;i<=n;i++) js[i]=js[i-1]*i%mod;
23 jsinv[n]=qpow(js[n],mod-2,mod);
24 for(int i=n-1;i>=0;i--) jsinv[i]=jsinv[i+1]*(i+1)%mod;
25 }
26 inline ll C(int n,int m)
27 {
28 return js[n]*jsinv[m]%mod*jsinv[n-m]%mod;
29 }
30 inline ll ask(int m)
31 {
32 ll ans=0;
33 for(int i=0,u=1;i<=m;i++,u=-u)
34 ans=(ans+u*C(m,i)*(qpow(2,qpow(2,m-i,mod-1),mod)-1)%mod)%mod;
35 return ans;
36 }
37 int main()
38 {
39 scanf("%d%d",&n,&k);
40 init();
41 printf("%lld\n",(ask(n-k)*C(n,k)%mod+mod)%mod);
42 return 0;
43 }
另一种等价的方法
$ans=\binom{n}{k}*\sum\limits_{i=k}^{n}(-1)^{i-k}*\binom{n-k}{i-k}*(2^{2^{n-i}}-1)$
这种方法可以理解为固定一种组合，从其他集合中选取几个进行容斥
也能算出答案
1 #include<iostream>
2 #include<cstdio>
3 #define ll long long
4 using namespace std;
5 const int mod=1e9+7;
6 int n,k;
7 ll js[1000010],jsinv[1000010];
8 ll qpow(ll base,int y,int mo)
9 {
10 ll ans=1;
11 while(y)
12 {
13 if(y&1) ans=ans*base%mo;
14 base=base*base%mo;
15 y>>=1;
16 }
17 return ans;
18 }
19 void init()
20 {
21 js[0]=1;
22 for(int i=1;i<=n;i++) js[i]=js[i-1]*i%mod;
23 jsinv[n]=qpow(js[n],mod-2,mod);
24 for(int i=n-1;i>=0;i--) jsinv[i]=jsinv[i+1]*(i+1)%mod;
25 }
26 inline ll C(int n,int m)
27 {
28 return js[n]*jsinv[m]%mod*jsinv[n-m]%mod;
29 }
30 int main()
31 {
32 scanf("%d%d",&n,&k);
33 init();
34 ll ans=0;
35 for(int i=k,u=1;i<=n;i++,u=-u)
36 ans=(ans+u*C(n-k,i-k)%mod*(qpow(2,qpow(2,n-i,mod-1),mod)-1)%mod)%mod;
37 printf("%lld\n",(ans*C(n,k)%mod+mod)%mod);
38 return 0;
39 }
