OpenCV探索之路（九）：模板匹配
模板匹配的作用在图像识别领域作用可大了。那什么是模板匹配？
模板匹配，就是在一幅图像中寻找另一幅模板图像最匹配（也就是最相似）的部分的技术。
说的有点抽象，下面给个例子说明就很明白了。
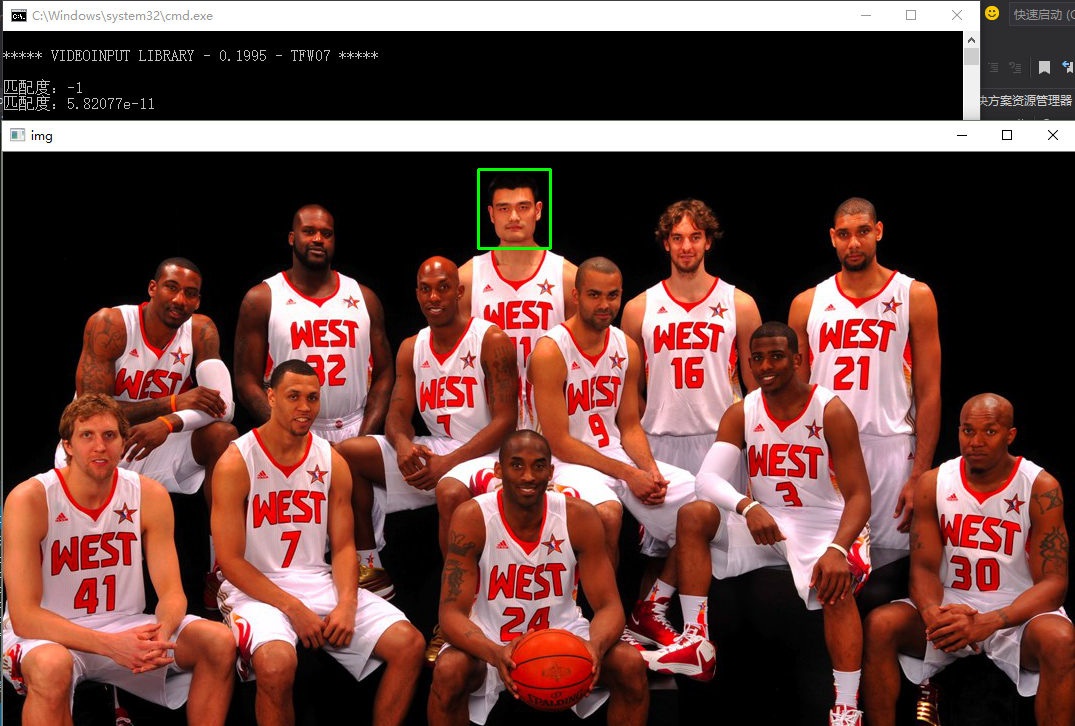
在上面这幅全明星照中，我们想找出姚明头像的位置，并把它标记出来，可以做到吗？
可以，这就是模板匹配的要做的事情。
其实模板匹配实现的思想也是很简单很暴力的，就是拿着模板图片（姚明头像）在原图（全明星照）中从左上至右下依次滑动，直到遇到某个区域的相似度低于我们设定的阈值，那么我们就认为该区域与模板匹配了，也就是我们找到了姚明的位置，并把它标记出来。
OpenCV中是通过MtachTemplate函数完成。
#include <opencv2/core/core.hpp>
#include <opencv2/imgproc/imgproc.hpp>
#include <opencv2/highgui/highgui.hpp>
#include <iostream>
#include <stdio.h>
using namespace std;
using namespace cv;
int main()
{
Mat img, templ, result;
img = imread("nba.jpg");
templ = imread("76.png");
int result_cols = img.cols - templ.cols + 1;
int result_rows = img.rows - templ.rows + 1;
result.create(result_cols, result_rows, CV_32FC1);
matchTemplate(img, templ, result, CV_TM_SQDIFF_NORMED);//这里我们使用的匹配算法是标准平方差匹配 method=CV_TM_SQDIFF_NORMED，数值越小匹配度越好
normalize(result, result, 0, 1, NORM_MINMAX, -1, Mat());
double minVal = -1;
double maxVal;
Point minLoc;
Point maxLoc;
Point matchLoc;
cout << "匹配度：" << minVal << endl;
minMaxLoc(result, &minVal, &maxVal, &minLoc, &maxLoc, Mat());
cout << "匹配度：" << minVal << endl;
matchLoc = minLoc;
rectangle(img, matchLoc, Point(matchLoc.x + templ.cols, matchLoc.y + templ.rows), Scalar(0, 255, 0), 2, 8, 0);
imshow("img", img);
waitKey(0);
return 0;
}
结果看来，大姚的头像位置确实被绿框标记出来了！很准！
我还在程序中特意打印出匹配度的最小值，因为我们知道这个算法是数值越小匹配度越高，由输出的结果看来这个数值还真的很小，说明匹配度真的相当高！
既然我们可以取得匹配度的数值，那我们是不是也可以利用该数值进行阈值对比呢？比如我想把在阈值范围之内的头像都标记出来。可以这么做：
//阈值判别，小于0.01才认为匹配成功，才将头像框出来
if (minVal < 0.001)
{
rectangle(img, matchLoc, Point(matchLoc.x + templ.cols, matchLoc.y + templ.rows), Scalar(0, 255, 0), 2, 8, 0);
}
同理，如果是数值越大表明匹配度越大的算法，就使用maxVal来对比就可以了。
上面的模板匹配我们使用了标准平方差匹配 CV_TM_SQDIFF_NORMED算法，看起来效果还不错，那还有其他算法吗？
问得好。OpenCV通过函数 matchTemplate 实现了模板匹配算法。可用的方法有6个:
通常，随着从简单的测量(平方差)到更复杂的测量(相关系数)，我们可获得越来越准确的匹配(同时也意味着越来越大的计算代价)。
最好的办法是对所有这些设置多做一些测试实验,以便为自己的应用选择同时兼顾速度和精度的最佳方案。
你想采用哪种算法，只需要将对应的传进函数matchTemplate里就可以了。
下面给出利用trackbar显示出多种模板那匹配算法的代码。
#include <opencv2/core/core.hpp>
#include <opencv2/imgproc/imgproc.hpp>
#include <opencv2/highgui/highgui.hpp>
#include <iostream>
using namespace cv;
using namespace std;
Mat g_srcImage, g_tempalteImage, g_resultImage;
int g_nMatchMethod;
int g_nMaxTrackbarNum = 5;
void on_matching(int, void*)
{
Mat srcImage;
g_srcImage.copyTo(srcImage);
int resultImage_cols = g_srcImage.cols - g_tempalteImage.cols + 1;
int resultImage_rows = g_srcImage.rows - g_tempalteImage.rows + 1;
g_resultImage.create(resultImage_cols, resultImage_rows, CV_32FC1);
matchTemplate(g_srcImage, g_tempalteImage, g_resultImage, g_nMatchMethod);
normalize(g_resultImage, g_resultImage, 0, 2, NORM_MINMAX, -1, Mat());
double minValue, maxValue;
Point minLocation, maxLocation, matchLocation;
minMaxLoc(g_resultImage, &minValue, &maxValue, &minLocation, &maxLocation);
if (g_nMatchMethod == TM_SQDIFF || g_nMatchMethod == CV_TM_SQDIFF_NORMED)
{
matchLocation = minLocation;
}
else
{
matchLocation = maxLocation;
}
rectangle(srcImage, matchLocation, Point(matchLocation.x + g_tempalteImage.cols, matchLocation.y + g_tempalteImage.rows), Scalar(0, 0, 255), 2, 8, 0);
rectangle(g_resultImage, matchLocation, Point(matchLocation.x + g_tempalteImage.cols, matchLocation.y + g_tempalteImage.rows), Scalar(0, 0, 255), 2, 8, 0);
imshow("原始图", srcImage);
imshow("效果图", g_resultImage);
}
int main()
{
g_srcImage = imread("nba.jpg");
if (!g_srcImage.data)
{
cout << "原始图读取失败" << endl;
return -1;
}
g_tempalteImage = imread("76.png");
if (!g_tempalteImage.data)
{
cout << "模板图读取失败" << endl;
return -1;
}
namedWindow("原始图", CV_WINDOW_AUTOSIZE);
namedWindow("效果图", CV_WINDOW_AUTOSIZE);
createTrackbar("方法", "原始图", &g_nMatchMethod, g_nMaxTrackbarNum, on_matching);
on_matching(0, NULL);
waitKey(0);
return 0;
}
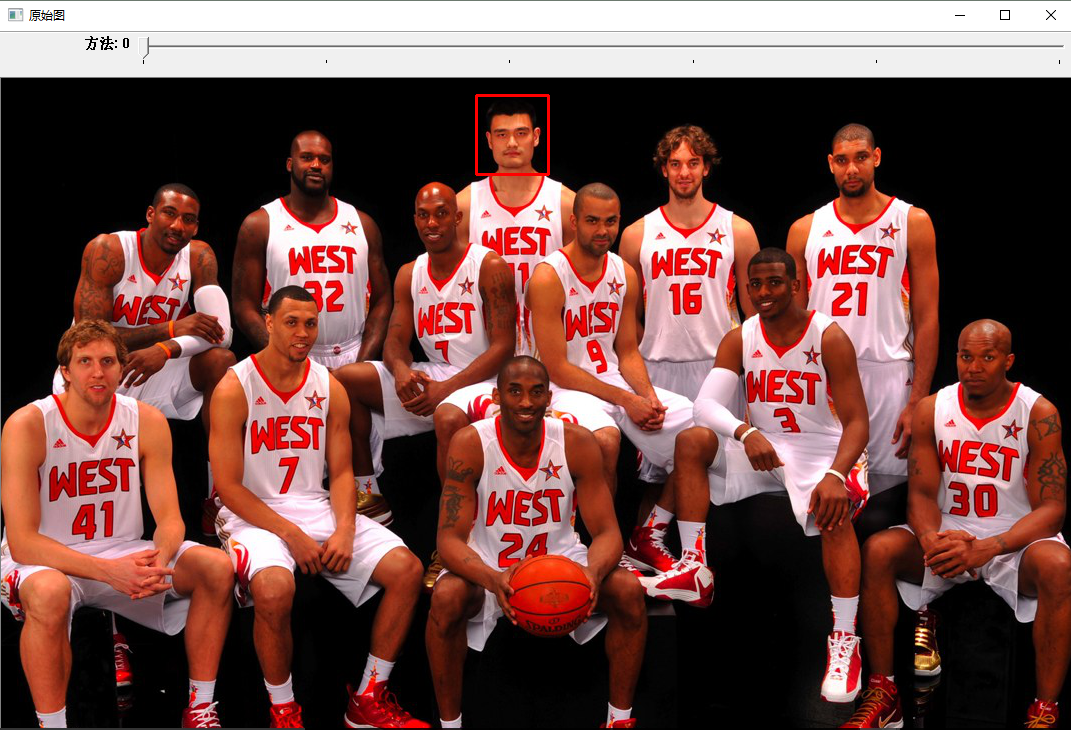
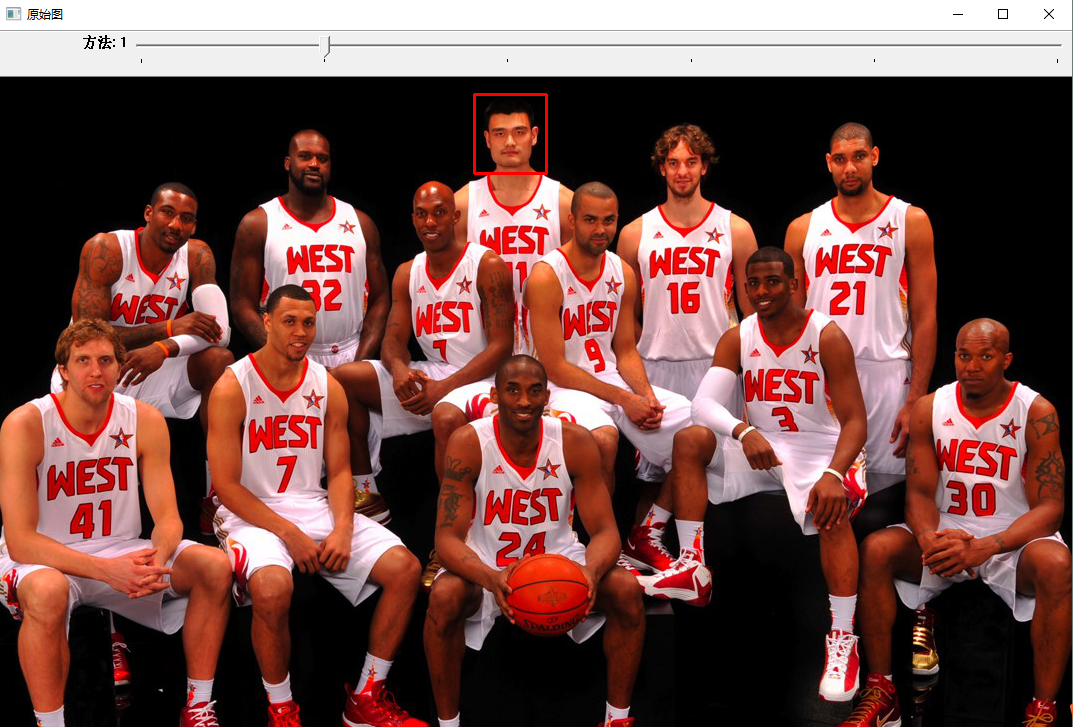
当然也会有一些算法匹配失败的.
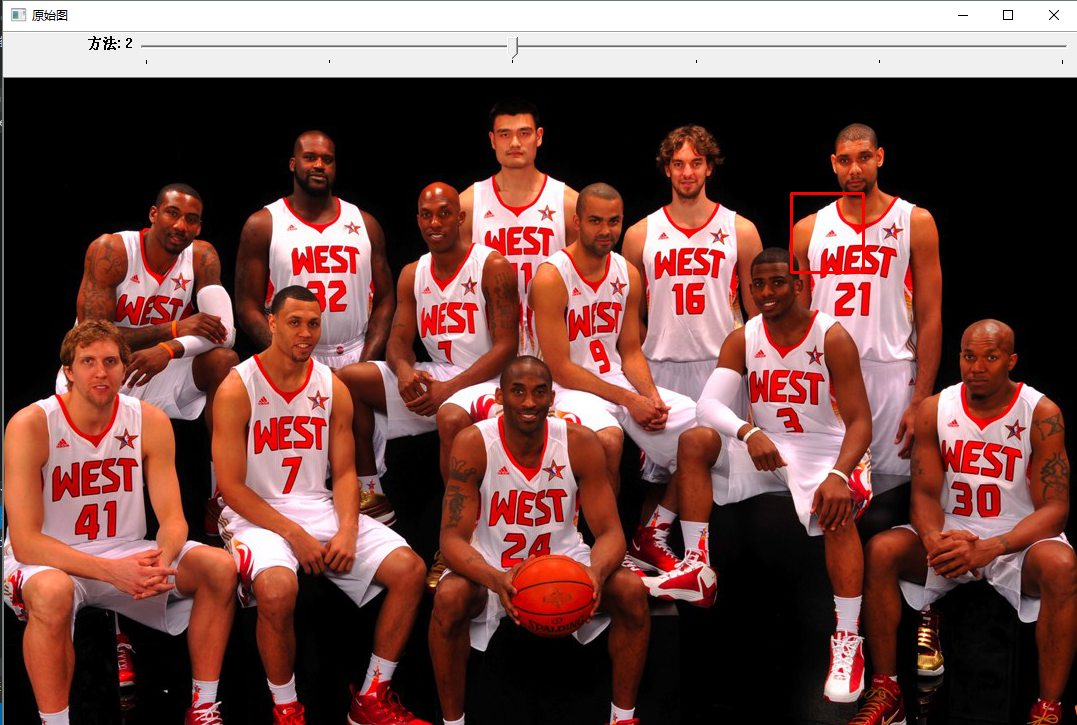
实验证明，该段程序效果很不错，但注意的是，模板配在原图抠出模板图的形式下准确率才比较高，不然的话可能准确度就不太高了。
那么模板匹配能在哪些项目有应用呢？我说一下我的经验。
最近我在参与实验室的一个项目，做的是发票的分类，分类的方法我首先采用的是模板匹配，也就是从一类发票中抠出一些特征区域，以此作为模板，自己设定阈值，低于阈值就是算是跟该类发票匹配了，就可以 对其进行分类。在我的测试看来，准确率还可以，不过也隐藏这一个比较大的隐患就是，一旦发票种类多了，比如100种，那么检测时间就会指数上升，这是不可取的。
