OpenCV探索之路（七）：霍夫变换
我们如何在图像中快速识别出其中的圆和直线？一个非常有效的方法就是霍夫变换，它是图像中识别各种几何形状的基本算法之一。
霍夫线变换
霍夫线变换是一种在图像中寻找直线的方法。OpenCV中支持三种霍夫线变换，分别是标准霍夫线变换、多尺度霍夫线变换、累计概率霍夫线变换。
在OpenCV中可以调用函数HoughLines来调用标准霍夫线变换和多尺度霍夫线变换。HoughLinesP函数用于调用累积概率霍夫线变换。
我们都知道，二维坐标轴上表示一条直线的方程式y = a*x + b，我们想求出一条直线就得想方设法求出其中的a和b的值。如果用极坐标来表示就是
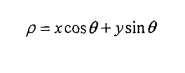
theta就是直线与水平线所成的角度，而rho就是圆的半径（也可以理解为原点到直线的距离），同样地，这两个参数也是表征一条直线的重要参数，确定他们俩了，也就确定一条直线了。正如下图所示。
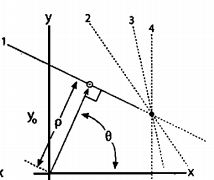
在OpenCV里，我们只需调用HoughLines就是可以得到表征一条直线的这两个参数值！
HoughLines用法
#include <iostream>
#include <opencv2\opencv.hpp>
#include <opencv2\imgproc\imgproc.hpp>
using namespace cv;
using namespace std;
int main()
{
Mat srcImage = imread("4.jpg");
imshow("Src Pic", srcImage);
Mat midImage, dstImage;
//边缘检测
Canny(srcImage, midImage, 50, 200, 3);
//灰度化
cvtColor(midImage, dstImage, CV_GRAY2BGR);
// 定义矢量结构存放检测出来的直线
vector<Vec2f> lines;
//通过这个函数，我们就可以得到检测出来的直线集合了
HoughLines(midImage, lines, 1, CV_PI / 180, 150, 0, 0);
//这里注意第五个参数，表示阈值，阈值越大，表明检测的越精准，速度越快，得到的直线越少（得到的直线都是很有把握的直线）
//这里得到的lines是包含rho和theta的，而不包括直线上的点，所以下面需要根据得到的rho和theta来建立一条直线
//依次画出每条线段
for (size_t i = 0; i < lines.size(); i++)
{
float rho = lines[i][0]; //就是圆的半径r
float theta = lines[i][1]; //就是直线的角度
Point pt1, pt2;
double a = cos(theta), b = sin(theta);
double x0 = a*rho, y0 = b*rho;
pt1.x = cvRound(x0 + 1000 * (-b));
pt1.y = cvRound(y0 + 1000*(a));
pt2.x = cvRound(x0 - 1000*(-b));
pt2.y = cvRound(y0 - 1000 * (a));
line(dstImage, pt1, pt2, Scalar(55, 100, 195), 1, LINE_AA); //Scalar函数用于调节线段颜色，就是你想检测到的线段显示的是什么颜色
imshow("边缘检测后的图", midImage);
imshow("最终效果图", dstImage);
}
waitKey();
return 0;
}
原图
阈值我设为250，看看直线检测的效果。你会发现，怎么图中一些很明显的的直线都没检测出来啊？原因是，我们阈值写的有点高了，只有那些有足够的把握认为是直线的直线才可能检测出来。
然后我把阈值改为150，直线检测效果就变成这样子了。显然多了很多直线，这是我们把我们的要求降低了，把那些“可能是直线”的直线都当做是直线了。所以，阈值的选择很重要，就看你是要精确查找还是模糊查找了。
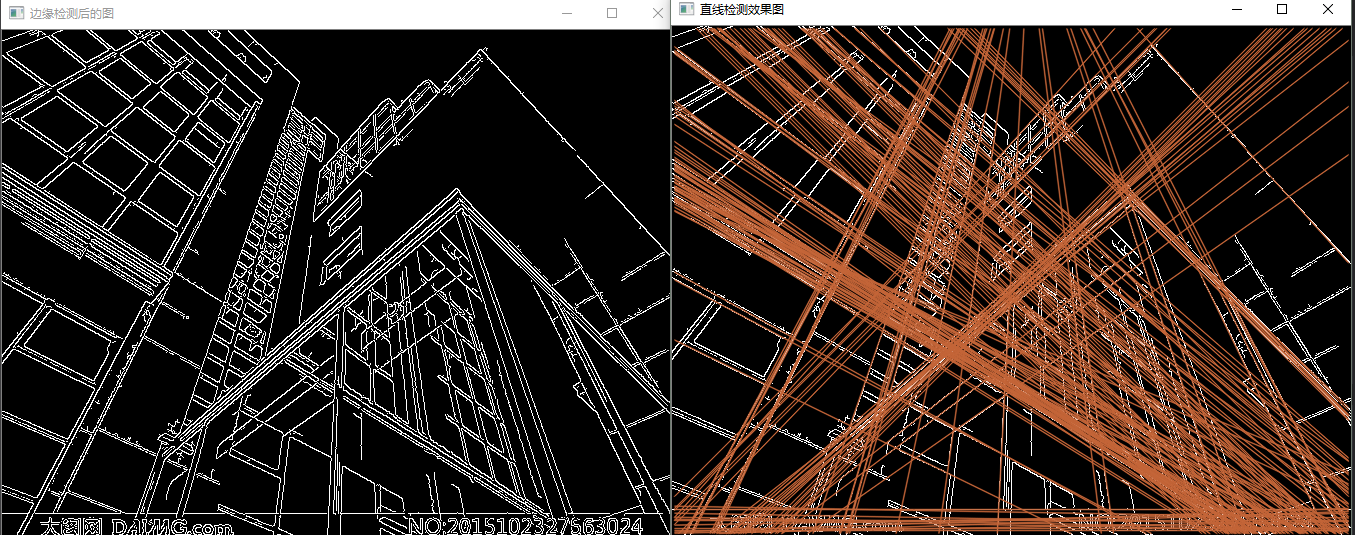
后来我又加了一句打印进去，想看看角度的单位是什么
cout << "line " << i << ": " << "rho:" << rho << " theta:" << theta << endl;
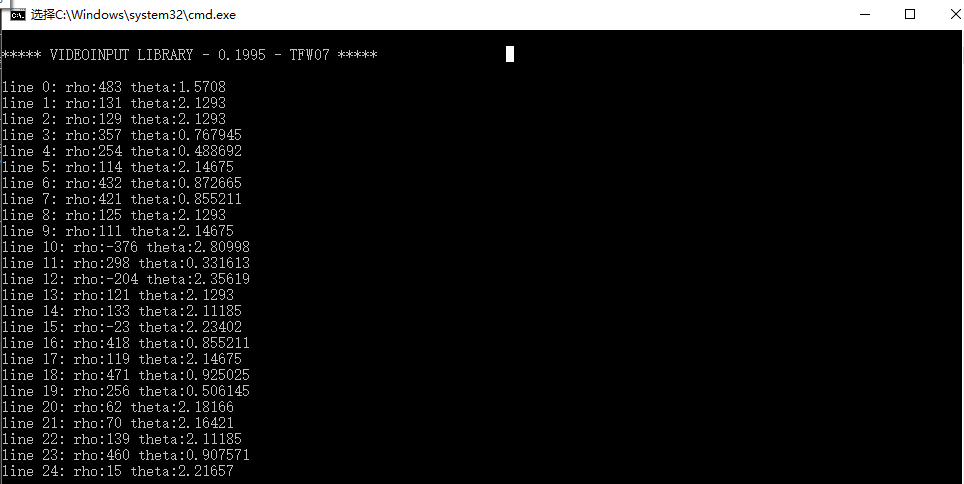
可以看到，角度theta用的单位不是我们所说的度数（70度、80度），而是数学上的π/2，π/3。
要想转为我们所说的度数，自己写个转换吧
float angle = theta / CV_PI * 180;
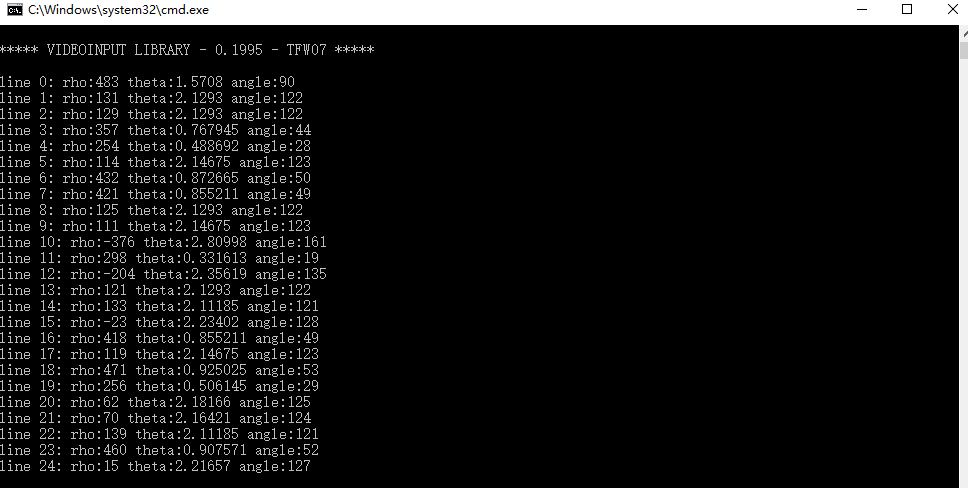
可以看出，转换后的角度范围就是我们想要的度数！值得注意的是，rho表示离坐标原点（就是图片左上角的点）的距离，theta是直线的旋转角度（0度表示垂直线，90度表示水平线）。
HoughLinesP用法
此函数在HoughLines的基础上在末尾加了一个代表Probabilistic（概率）的P，表明使用的是累计概率变换。
#include <iostream>
#include <opencv2\opencv.hpp>
#include <opencv2\imgproc\imgproc.hpp>
using namespace cv;
using namespace std;
int main()
{
Mat srcImage = imread("2.jpg");
imshow("Src Pic", srcImage);
Mat midImage, dstImage;
Canny(srcImage, midImage, 50, 200, 3);
cvtColor(midImage, dstImage, CV_GRAY2BGR);
vector<Vec4i> lines;
//与HoughLines不同的是，HoughLinesP得到lines的是含有直线上点的坐标的，所以下面进行划线时就不再需要自己求出两个点来确定唯一的直线了
HoughLinesP(midImage, lines, 1, CV_PI / 180, 80, 50, 10);//注意第五个参数，为阈值
//依次画出每条线段
for (size_t i = 0; i < lines.size(); i++)
{
Vec4i l = lines[i];
line(dstImage, Point(l[0], l[1]), Point(l[2], l[3]), Scalar(186, 88, 255), 1, LINE_AA); //Scalar函数用于调节线段颜色
imshow("边缘检测后的图", midImage);
imshow("最终效果图", dstImage);
}
waitKey();
return 0;
}
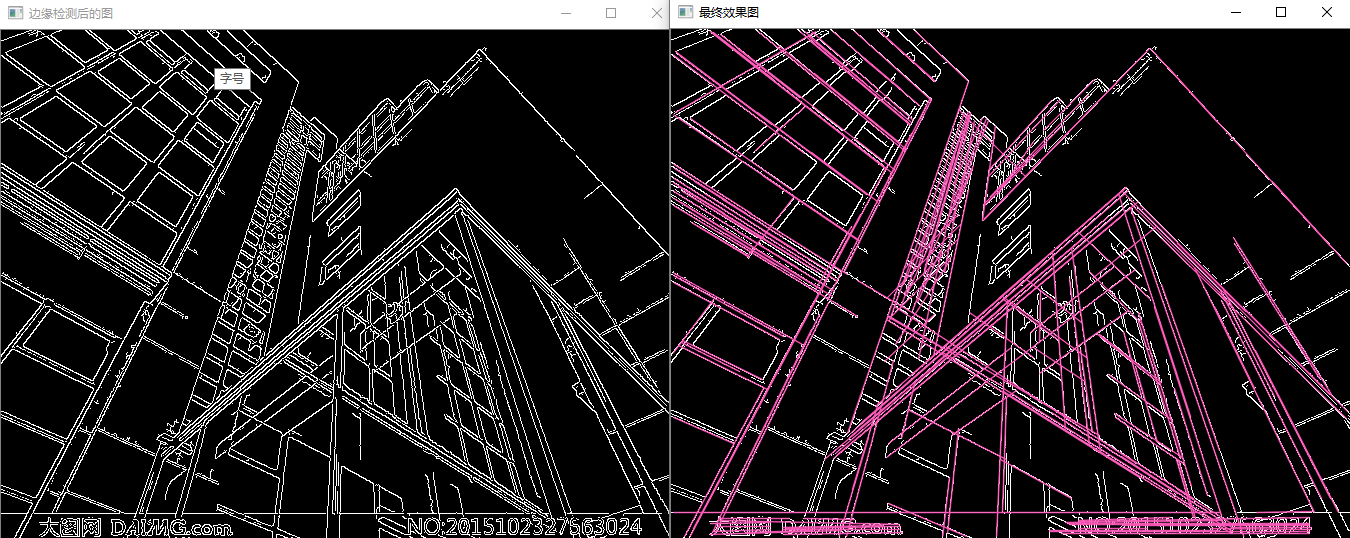
貌似效果还不错。
霍夫圆变换
刚刚的霍夫变换是检测直线的，如果我们想检测圆形，那该怎么办？那就用霍夫圆变换！用法也大同小异。
#include <iostream>
#include <opencv2\opencv.hpp>
#include <opencv2\imgproc\imgproc.hpp>
using namespace cv;
using namespace std;
int main()
{
Mat srcImage = imread("test5.jpg");
Mat midImage, dstImage;//临时变量和目标图的定义
imshow("【原始图】", srcImage);
//【3】转为灰度图，进行图像平滑
cvtColor(srcImage, midImage, CV_BGR2GRAY);//转化边缘检测后的图为灰度图
GaussianBlur(midImage, midImage, Size(9, 9), 2, 2);
//【4】进行霍夫圆变换
vector<Vec3f> circles;
HoughCircles(midImage, circles, CV_HOUGH_GRADIENT, 1.5, 10, 200, 150, 0, 0); //注意第七的参数为阈值，可以自行调整，值越大，检测的圆更精准
//【5】依次在图中绘制出圆
for (size_t i = 0; i < circles.size(); i++)
{
Point center(cvRound(circles[i][0]), cvRound(circles[i][1]));
int radius = cvRound(circles[i][2]);
//绘制圆心
circle(srcImage, center, 3, Scalar(0, 255, 0), -1, 8, 0);
//绘制圆轮廓
circle(srcImage, center, radius, Scalar(155, 50, 255), 3, 8, 0);
}
//【6】显示效果图
imshow("【效果图】", srcImage);
waitKey(0);
return 0;
}
可以看到，有一些圆没有检测出来，同时还有一些不是圆形的确有误以为是圆形了，说明阈值选择不是很妥当。
另外提一点，霍夫圆变换的检测速度真的慢，显然进行圆检测的计算量还真不少！
