[回归问题] 逻辑回归，线性回归

回归问题概括：

1） 数据

2） 假设的模型，即一个含有未知的参数的函数。通过学习，可以估计出参数。然后利用这个模型去预测/分类新的数据

 

回归和分类：

• 都属于有监督的学习
• 分类返回的是明确的类别信息，0 or 1，是 or 否
• 回归返回的是，某一个值或者范围的取值概率。如果把概率大小跟最终类别关联起来，就是分类。

线性回归：

线性回归假设特征和结果都满足线性，即变量都是一次方。预测模型是一个线性函数：

    

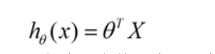
求解思想：求参数，使得损失函数(square error)最小，即达到最优。

      

线性回归的代码实例：

import org.apache.spark.mllib.regression.LabeledPoint
import org.apache.spark.mllib.regression.LinearRegressionModel
import org.apache.spark.mllib.regression.LinearRegressionWithSGD
import org.apache.spark.mllib.linalg.Vectors

// 获取数据
val data = sc.textFile("data/mllib/ridge-data/lpsa.data")
val parsedData = data.map { line =>
  val parts = line.split(',')
  LabeledPoint(parts(0).toDouble, Vectors.dense(parts(1).split(' ').map(_.toDouble)))
}.cache()

//训练模型
val numIterations = 100
val stepSize = 0.00000001
val model = LinearRegressionWithSGD.train(parsedData, numIterations, stepSize)

// 评价
val valuesAndPreds = parsedData.map { point =>
  val prediction = model.predict(point.features)
  (point.label, prediction)
}
val MSE = valuesAndPreds.map{case(v, p) => math.pow((v - p), 2)}.mean()
println("training Mean Squared Error = " + MSE)

 

逻辑回归

是线性回归的进化，复杂化？套用一个Sigmoid函数：

                    

预测函数是：

  

但，逻辑回归是一种减小预测范围，将预测值限定为 [0,1] 间的一种回归模型。上面的预测函数表示，结果为1的概率。

因此逻辑回归的模型和求解依赖于极大似然估计：

         

取对数后，即可求得theta.

 

逻辑回归的使用代码：

import org.apache.spark.SparkContext
import org.apache.spark.mllib.classification.{LogisticRegressionWithLBFGS, LogisticRegressionModel}
import org.apache.spark.mllib.evaluation.MulticlassMetrics
import org.apache.spark.mllib.regression.LabeledPoint
import org.apache.spark.mllib.linalg.Vectors
import org.apache.spark.mllib.util.MLUtils

// 加载训练数据
val data = MLUtils.loadLibSVMFile(sc, "data/mllib/sample_libsvm_data.txt")
// 切分数据，training (60%) and test (40%).
val splits = data.randomSplit(Array(0.6, 0.4), seed = 11L)
val training = splits(0).cache()
val test = splits(1)

// 训练模型
val model = new LogisticRegressionWithLBFGS()
  .setNumClasses(10)
  .run(training)
// Compute raw scores on the test set.
val predictionAndLabels = test.map { case LabeledPoint(label, features) =>
  val prediction = model.predict(features)
  (prediction, label)
}

// Get evaluation metrics.
val metrics = new MulticlassMetrics(predictionAndLabels)
val precision = metrics.precision
println("Precision = " + precision)

// 保存和加载模型
model.save(sc, "myModelPath")
val sameModel = LogisticRegressionModel.load(sc, "myModelPath")