1. 码制与逻辑函数化简(数电)
1. 码制
- 反码与补码
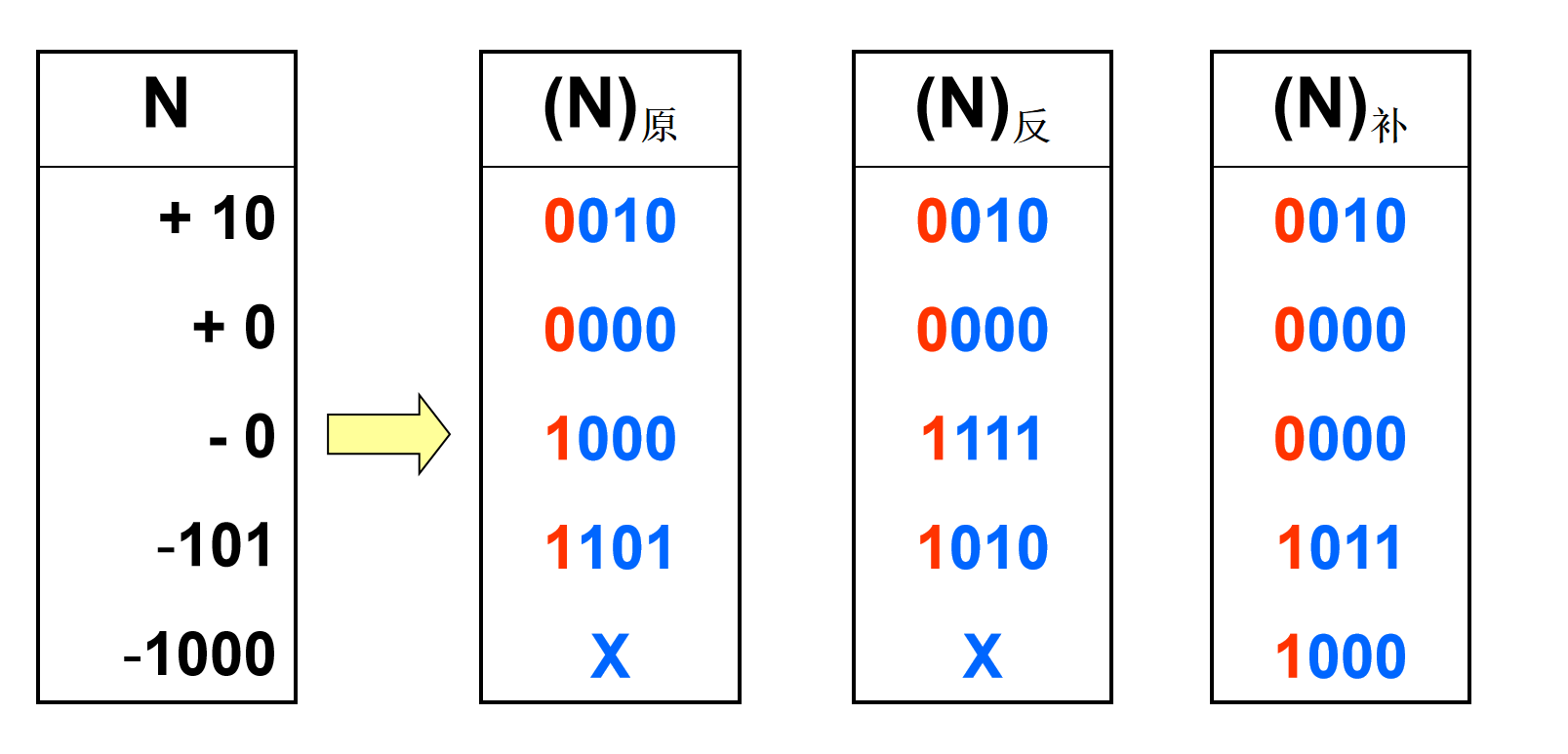
负数反码正取反,补码再+1
a. (X-Y)补=X补+(-Y)补=X补-Y反+1
如7-3=0111-0011=0100
在计算机中用补码减法,0111+1100+1=01000
可以这样来看:0111-0011=0111+1100+1等价于1100+1+0011=0
所以Y+(-Y)补=0,即-Y=+(-Y补)
b. 补码的表示范围为 -2(n-1)~2(n-1)-1
(-1) + (-127) = [1000 0001]原 + [1111 1111]原 = [1111 1111]补 + [1000 0001]补 = [1000 0000]补
-1-127的结果应该是-128, 在用补码运算的结果中, [1000 0000]补 就是-128.但是注 意因为实际上是使用以前的-0的补码来表示-128, 所以-128并没有原码和反码表示.(对-128的补码表示[10000000]补算出来的原码是[0000 0000]原, 这是不正确的) - Hamming码:存储校正
2^i 处Ci配偶时,满足2^i, 2^i +1,...2^(i+1)-1,...(1数目=2k), - CRC码:用于循环冗余较正,
M(x)* x^k=G(x)* Q(x)+R(x),满足(M(x)* x^k+R(X))/G(x)==Q(x);
PS: 不是常规的除法 - BCD码:
- 每位10进制用4位2进制表示
- 为-末尾添上1100,+添上1101,10进制数表示成4位2进制最多到0101,以此区分奇偶
- 偶数首数前补0000因为正常数不可能以0开头,来区分偶数
- 进一步修改BCD码来校验奇偶,在每一个表示10进制数的4位2进制前补一个校验位,make the number of 1 odd/even
- 格雷码的一种构造思路:
先给出2位的 00,01,11,10
假设我们有n位格雷码的构造序列p={a1,a2,..,an}
对n+1位,首先沿用n位的,再在an后补上{1,an},之后利用n位构造的逆序列,补上
{{1,an},{1,a(n-1)},...{1,a1}},bingo!
- 格雷码与二进制码的转化:
2. 逻辑代数
- 运算 satisfy 反演(运算+常量+变量),对偶(运算+常量)律(此为格的性质)
- 开关函数的+、·、反分别对应∪、∩,反,熟知小项表达式
最小项—与;最大项 - 布尔代数(系统)(——最大小元分别为1,0的有补分配格)与表达式
- 所有开关函数都为布尔代数
- 同构定理与原子表示
- 代数化简公式(先用卡诺图得出结果)


3.逻辑函数的形式变换
转成与或式容易
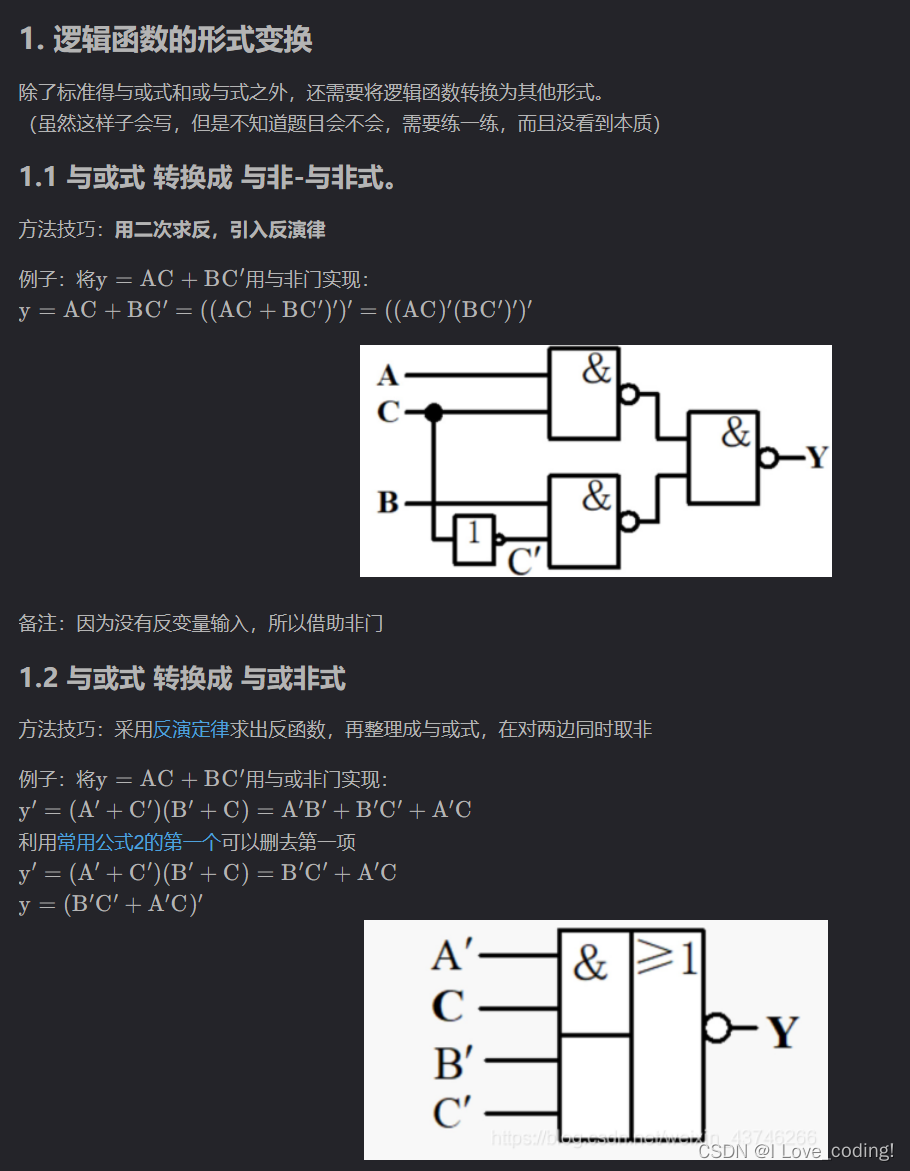
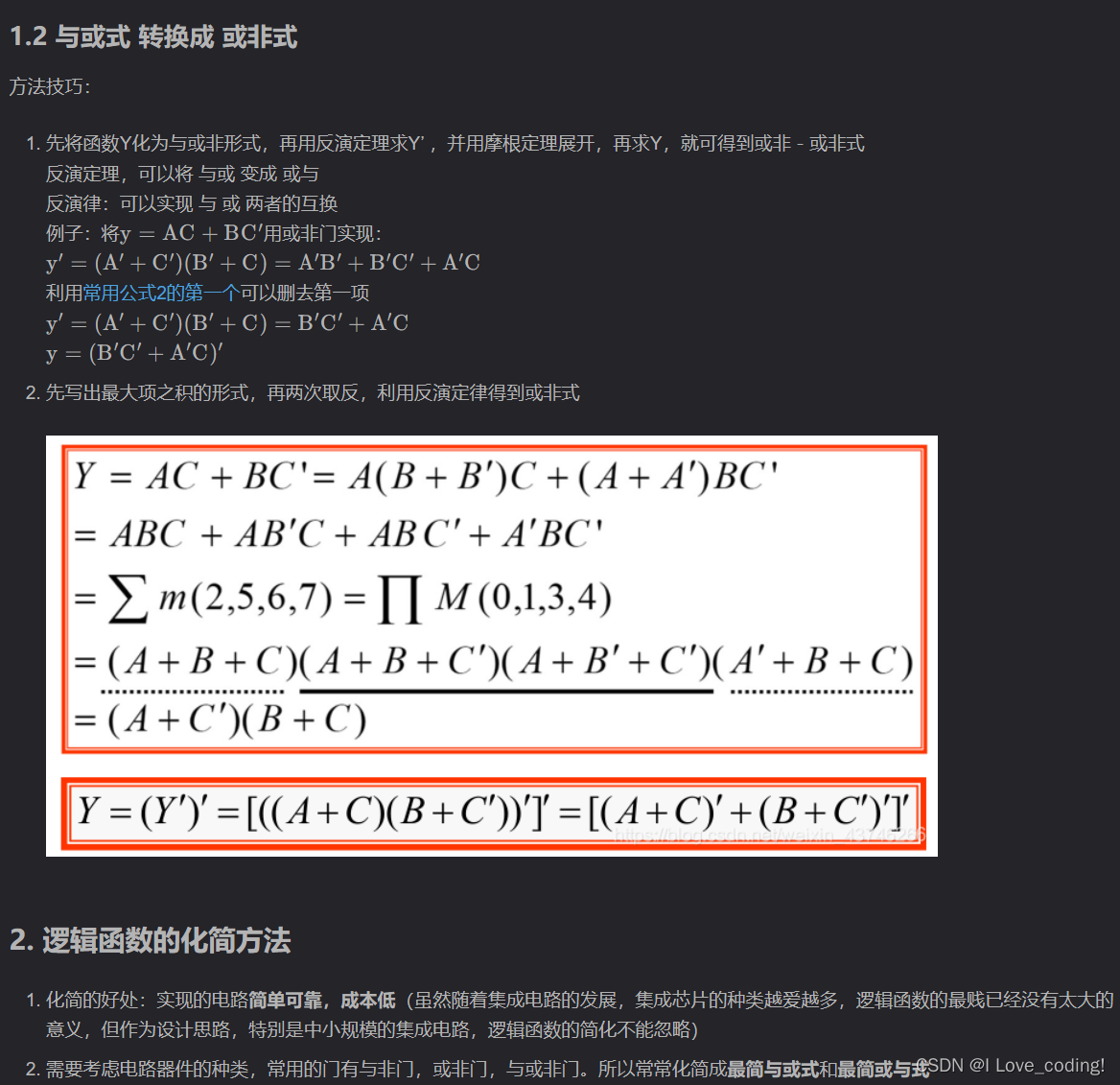
4.卡诺图(http://t.csdn.cn/0FUUM)
- 圈数最少,圈可重叠
Q1. 如何化简为异或式
Q2. 同或/异或符号
愿偿少年泪,犹趁未老时!
本文来自博客园,作者:clfire,转载请注明原文链接:https://www.cnblogs.com/sky1water/p/16720550.html


