结构体对齐详解【转】
转自：https://www.cnblogs.com/motadou/archive/2009/01/17/1558438.html
许多实际的计算机系统对基本类型数据在内存中存放的位置有限制，它们会要求这些数据的起始地址的值是某个数k的倍数，这就是所谓的内存对齐，而这个k则被称为该数据类型的对齐模数(alignment modulus)。这种强制的要求一来简化了处理器与内存之间传输系统的设计，二来可以提升读取数据的速度。
比如这么一种处理器，它每次读写内存的时候都从某个8倍数的地址开始，一次读出或写入8个字节的数据，假如软件能保证double类型的数据都从8倍数地址开始，那么读或写一个double类型数据就只需要一次内存操作。否则，我们就可能需要两次内存操作才能完成这个动作，因为数据或许恰好横跨在两个符合对齐要求的8字节内存块上。
1)结构体总长度；
2)结构体内各数据成员的内存对齐，即该数据成员相对结构体的起始位置；
1)将结构体内所有数据成员的长度值相加，记为sum_a；
2)将各数据成员为了内存对齐，按各自对齐模数而填充的字节数累加到和sum_a上，记为sum_b。对齐模数是#pragma pack指定的数值以及该数据成员自身长度中数值较小者。该数据相对起始位置应该是对齐模式的整数倍;
3)将和sum_b向结构体模数对齐，该模数是【#pragma pack指定的数值】、【未指定#pragma pack时，系统默认的对齐模数（32位系统为4字节，64位为8字节）】和【结构体内部最大的基本数据类型成员】长度中数值较小者。结构体的长度应该是该模数的整数倍。
在计算之前，我们首先需要明确的是各个数据成员的对齐模数，对齐模数和数据成员本身的长度以及pragma pack编译参数有关，其值是二者中最小数。如果程序没有明确指出，就需要知道编译器默认的对齐模数值。下表是Windows XP/DEV-C++和Linux/GCC中基本数据类型的长度和默认对齐模数。
| char | short | int | long | float | double | long long | long double | ||
| Win-32 | 长度 | 1 | 2 | 4 | 4 | 4 | 8 | 8 | 8 |
| 模数 | 1 | 2 | 4 | 4 | 4 | 8 | 8 | 8 | |
| Linux-32 | 长度 | 1 | 2 | 4 | 4 | 4 | 8 | 8 | 12 |
| 模数 | 1 | 2 | 4 | 4 | 4 | 4 | 4 | 4 | |
| Linux-64 | 长度 | 1 | 2 | 4 | 8 | 4 | 8 | 8 | 16 |
| 模数 | 1 | 2 | 4 | 8 | 4 | 8 | 8 | 16 |
例子1：
struct my_struct
{
char a;
long double b;
};
此例子Windows和Linux计算方法有些许不一致。
在Windows中计算步骤如下：
步骤1：所有数据成员自身长度和：1B + 8B = 9B --> sum_a = 9B
步骤2：数据成员a放在相对偏移0处，之前不需要填充字节；数据成员b为了内存对齐，根据“结构体大小的计算方法和步骤”中第二条原则，其对齐模数是8，之前需填充7个字节，sum_a + 7 = 16B --> sum_b = 16 B
步骤3：按照定义，结构体对齐模数是结构体内部最大数据成员长度和pragma pack中较小者，前者为8后者为4，所以结构体对齐模数是4。sum_b是4的4倍，不需再次对齐。
综上3步，可知结构体的长度是16B，各数据成员在内存中的分布如图1-1所示。
在Linux中计算步骤如下：
步骤1：所有数据成员自身长度和：1B + 12B = 13B --> sum_a = 13B
步骤2：数据成员a放在相对偏移0处，之前不需要填充字节；数据成员b为了内存对齐，根据“结构体大小的计算方法和步骤”中第二条原则，其对齐模数是4，之前需填充3个字节，sum_a + 3 = 16B --> sum_b = 16 B
步骤3：按照定义，结构体对齐模数是结构体内部最大数据成员长度和pragma pack中较小者，前者为12后者为4，所以结构体对齐模数是4。sum_b是4的4倍，不需再次对齐。
综上3步，可知结构体的长度是16B，各数据成员在内存中的分布如图1-2所示。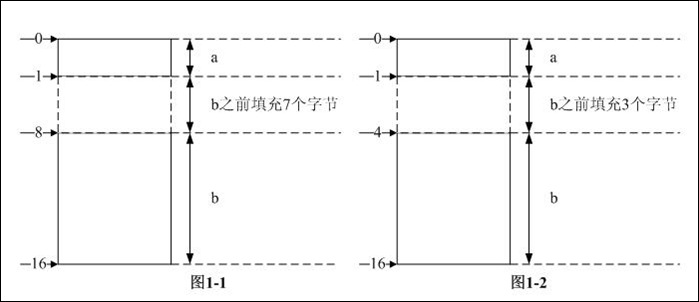 
例子2：
#pragma pack(2)
struct my_struct
{
char a;
long double b;
};
#pragma pack()
例子1和例子2不同之处在于例子2中使用了#pragma pack(2)编译参数，它强制指定对齐模数是2。此例子Windows和Linux计算方法有些许不一致。
在Windows中计算步骤如下：
步骤1：所有数据成员自身长度和：1B + 8B = 13B --> sum_a = 9B
步骤2：数据成员a放在相对偏移0处，之前不需要填充字节；数据成员b为了内存对齐，根据“结构体大小的计算方法和步骤”中第二条原则，其对齐模数是2，之前需填充1个字节，sum_a + 1 = 10B --> sum_b = 10 B
步骤3：按照定义，结构体对齐模数是结构体内部最大数据成员长度和pragma pack中较小者，前者为8后者为2，所以结构体对齐模数是2。sum_b是2的5倍，不需再次对齐。
综上3步，可知结构体的长度是10B，各数据成员在内存中的分布如图2-1所示。
在Linux中计算步骤如下：
步骤1：所有数据成员自身长度和：1B + 12B = 13B --> sum_a = 13B
步骤2：数据成员a放在相对偏移0处，之前不需要填充字节；数据成员b为了内存对齐，根据“结构体大小的计算方法和步骤”中第二条原则，其对齐模数是2，之前需填充1个字节，sum_a + 1 = 14B --> sum_b = 14 B
步骤3：按照定义，结构体对齐模数是结构体内部最大数据成员长度和pragma pack中较小者，前者为8后者为2，所以结构体对齐模数是2。sum_b是2的7倍，不需再次对齐。
综上3步，可知结构体的长度是14B，各数据成员在内存中的分布如图2-2所示。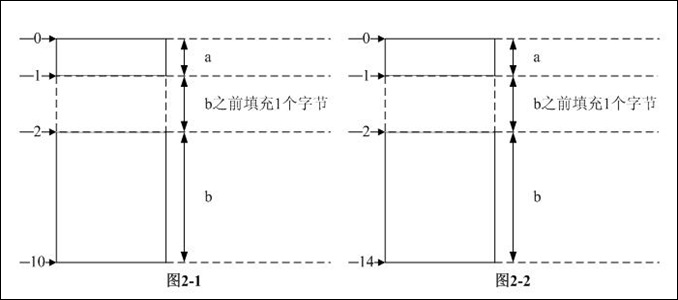 
例子3：
struct my_struct
{
char a;
double b;
char c;
};
前两例中，数据成员在Linux和Windows下都相同，例3中double的对齐模数在Linux中是4，在Windows下是8，针对这种模数不相同的情况加以分析。
在Windows中计算步骤如下：
步骤1：所有数据成员自身长度和：1B + 8B + 1B = 10B --> sum_a = 10B
步骤2：数据成员a放在相对偏移0处，之前不需要填充字节；数据成员b为了内存对齐，根据“结构体大小的计算方法和步骤”中第二条原则，其对齐模数是8，之前需填充7个字节，sum_a + 7 = 17B --> sum_b = 17B
步骤3：按照定义，结构体对齐模数是结构体内部最大数据成员长度和pragma pack中较小者，前者为8后者为8，所以结构体对齐模数是8。sum_b应该是8的整数倍，所以要在结构体后填充8*3 - 17 = 7个字节。
综上3步，可知结构体的长度是24B，各数据成员在内存中的分布如图3-1所示。
在Linux中计算步骤如下：
步骤1：所有数据成员自身长度和：1B + 8B + 1B = 10B，sum_a = 10B
步骤2：数据成员a放在相对偏移0处，之前不需要填充字节；数据成员b为了内存对齐，根据“结构体大小的计算方法和步骤”中第二条原则，其对齐模数是4，之前需填充3个字节，sum_b = sum_a + 3 = 13B
步骤3：按照定义，结构体对齐模数是结构体内部最大数据成员长度和pragma
pack中较小者，前者为8后者为4，所以结构体对齐模数是4。sum_b应该是4的整数倍，所以要在结构体后填充4*4 - 13 = 3个字节。
综上3步，可知结构体的长度是16B，各数据成员在内存中的分布如图3-2所示。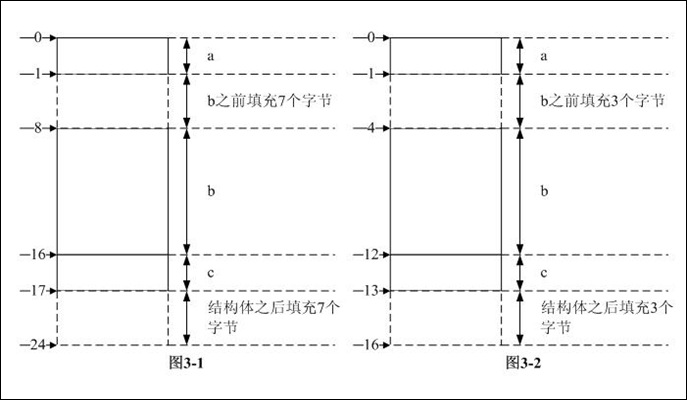 
例子4：
struct my_struct
{
char a[11];
int b;
char c;
};
此例子Windows和Linux计算方法一样，如下：
步骤1：所有数据成员自身长度和：11B + 4B + 1B = 16B --> sum_a = 16B
步骤2：数据成员a放在相对偏移0处，之前不需要填充字节；数据成员b为了内存对齐，根据“结构体大小的计算方法和步骤”中第二条原则，其对齐模数是4，之前需填充3个字节，sum_a + 1 = 17B --> sum_b = 17B
步骤3：按照定义，结构体对齐模数是结构体内部最大数据成员长度和pragma pack中较小者，前者为4后者为4，所以结构体对齐模数是4。sum_b是4的整数倍，需在结构体后填充4*5 - 17 = 1个字节。
综上3步，可知结构体的长度是20B，各数据成员在内存中的分布如图4所示。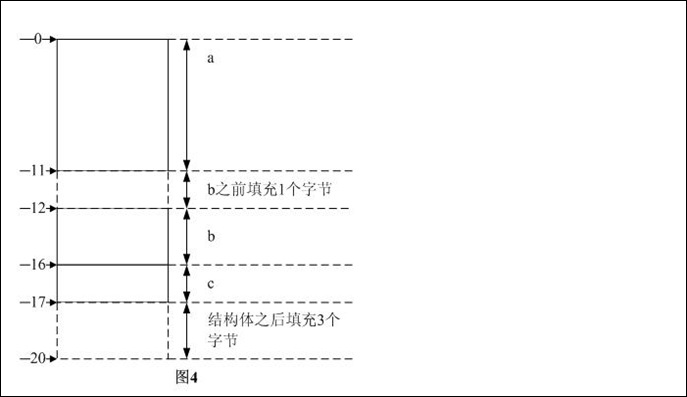 
例子5：
struct my_test
{
int my_test_a;
char my_test_b;
};
struct my_struct
{
struct my_test a;
double my_struct_a;
int my_struct_b;
char my_struct_c;
};
例子5和前几个例子均不同，在此例子中我们要计算struct my_struct的大小，而my_struct中嵌套了一个my_test结构体。这种结构体应该如何计算呢？原则是将my_test在my_struct中先展开，然后再计算，即是展开成如下结构体：
struct my_struct
{
int my_test_a;
char my_test_b;
double my_struct_a;
int my_struct_b;
char my_struct_c;
};
此例子Windows中的计算方法如下：
步骤1：所有数据成员自身长度和：4B + 1B + 8B + 4B + 1B= 18B --> sum_a = 18B
步骤2：数据成员my_struct_a为了内存对齐，根据“结构体大小的计算方法和步骤”中第二条原则，其对齐模数是8，之前需填充3个字节：sum_a + 3 = 21B --> sum_b = 21B
步骤3：按照定义，结构体对齐模数是结构体内部最大数据成员长度和pragma pack中较小者，前者为8后者为8，所以结构体对齐模数是8。sum_b是8的整数倍，需在结构体后填充3*8 - 21 = 3个字节。
综上3步，可知结构体的长度是24B，各数据成员在内存中的分布如图5所示。
此例子Linux中的计算方法如下：
步骤1：所有数据成员自身长度和：4B + 1B + 8B + 4B + 1B= 18B，sum_a = 18B
步骤2：数据成员my_struct_a为了内存对齐，根据“结构体大小的计算方法和步骤”中第二条原则，其对齐模数是4，之前需填充3个字节，sum_b = sum_a + 3 = 21B
步骤3：按照定义，结构体对齐模数是结构体内部最大数据成员长度和pragma
pack中较小者，前者为4后者为4，所以结构体对齐模数是4。sum_b是4的整数倍，需在结构体后填充6*4 - 21 = 3个字节。
综上3步，可知结构体的长度是24B，各数据成员在内存中的分布如图5所示。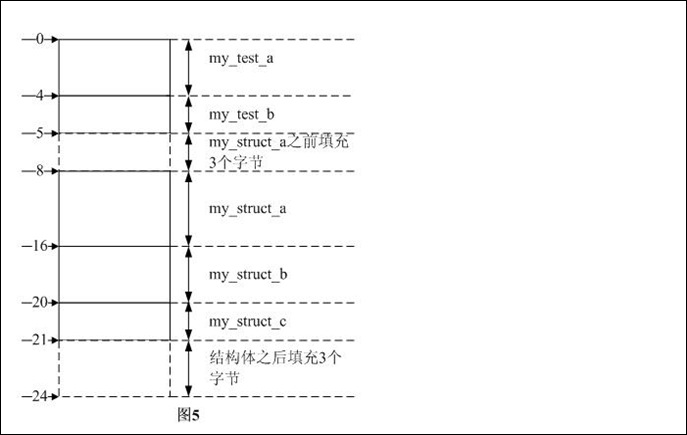 
上面的例子均在Windows(VC++6.0)和Linux(GCC4.1.0)上测试验证。下面是测试程序。
#include <iostream>
#include <stdio.h>
using namespace std;
int main()
{
cout << "sizeof(char) = " << sizeof(char) << endl;
cout << "sizeof(short) = " << sizeof(short) << endl;
cout << "sizeof(int) = " << sizeof(int) << endl;
cout << "sizeof(long) = " << sizeof(long) << endl;
cout << "sizeof(float) = " << sizeof(float) << endl;
cout << "sizeof(double) = " << sizeof(double) << endl;
cout << "sizeof(long long) = " << sizeof(long long) << endl;
cout << "sizeof(long double) = " << sizeof(long double) << endl << endl;
// 例子1
{
struct my_struct
{
char a;
long double b;
};
cout << "exapmle-1: sizeof(my_struct) = " << sizeof(my_struct) << endl;
struct my_struct data;
printf("my_struct->a: %u\nmy_struct->b: %u\n\n", &data.a, &data.b);
}
// 例子2
{
#pragma pack(2)
struct my_struct
{
char a;
long double b;
};
#pragma pack()
struct my_struct data;
cout << "exapmle-2: sizeof(my_struct) = " << sizeof(my_struct) << endl;
printf("my_struct->a: %u\nmy_struct->b: %u\n\n", &data.a, &data.b);
}
// 例子3
{
struct my_struct
{
char a;
double b;
char c;
};
struct my_struct data;
cout << "exapmle-3: sizeof(my_struct) = " << sizeof(my_struct) << endl;
printf("my_struct->a: %u\nmy_struct->b: %u\nmy_struct->c: %u\n\n", &data.a, &data.b, &data.c);
}
// 例子4
{
struct my_struct
{
char a[11];
int b;
char c;
};
cout << "example-4: sizeof(my_struct) = " << sizeof(struct my_struct) << endl;
struct my_struct data;
printf("my_struct->a: %u\nmy_struct->b: %u\nmy_struct->c: %u\n\n", &data, &data.b, &data.c);
}
// 例子5
{
struct my_test
{
int my_test_a;
char my_test_b;
};
struct my_struct
{
struct my_test a;
double my_struct_a;
int my_struct_b;
char my_struct_c;
};
cout << "example-5: sizeof(my_struct) = " << sizeof(struct my_struct) << endl;
struct my_struct data;
printf("my_struct->my_test_a : %u\n"
"my_struct->my_test_b : %u\n"
"my_struct->my_struct_a: %u\n"
"my_struct->my_struct_b: %u\n"
"my_struct->my_struct_c: %u\n", &data.a.my_test_a, &data.a.my_test_b,
&data.my_struct_a, &data.my_struct_b, &data.my_struct_c);
}
return 0;
}
执行结果：
//Linux localhost 3.4.6-2.10-desktop #1 SMP PREEMPT Thu Jul 28 19:20:26 UTC 2012 (641c197) x86_64 x86_64 x86_64 GNU/Linux
sizeof(char) = 1
sizeof(short) = 2
sizeof(int) = 4
sizeof(long) = 8
sizeof(float) = 4
sizeof(double) = 8
sizeof(long long) = 8
sizeof(long double) = 16
exapmle-1: sizeof(my_struct) = 32
my_struct->a: 2163695552
my_struct->b: 2163695568
exapmle-2: sizeof(my_struct) = 18
my_struct->a: 2163695680
my_struct->b: 2163695682
exapmle-3: sizeof(my_struct) = 24
my_struct->a: 2163695648
my_struct->b: 2163695656
my_struct->c: 2163695664
example-4: sizeof(my_struct) = 20
my_struct->a: 2163695616
my_struct->b: 2163695628
my_struct->c: 2163695632
example-5: sizeof(my_struct) = 24
my_struct->my_test_a : 2163695584
my_struct->my_test_b : 2163695588
my_struct->my_struct_a: 2163695592
my_struct->my_struct_b: 2163695600
my_struct->my_struct_c: 2163695604
//Linux localhost 3.4.6-2.10-desktop #1 SMP PREEMPT Thu Jul 26 09:36:26 UTC 2012 (641c197) i686 i686 i386 GNU/Linux
sizeof(char) = 1
sizeof(short) = 2
sizeof(int) = 4
sizeof(long) = 4
sizeof(float) = 4
sizeof(double) = 8
sizeof(long long) = 8
sizeof(long double) = 12
exapmle-1: sizeof(my_struct) = 16
my_struct->a: 3213889904
my_struct->b: 3213889908
exapmle-2: sizeof(my_struct) = 14
my_struct->a: 3213889890
my_struct->b: 3213889892
exapmle-3: sizeof(my_struct) = 16
my_struct->a: 3213889872
my_struct->b: 3213889876
my_struct->c: 3213889884
example-4: sizeof(my_struct) = 20
my_struct->a: 3213889852
my_struct->b: 3213889864
my_struct->c: 3213889868
example-5: sizeof(my_struct) = 24
my_struct->my_test_a : 3213889828
my_struct->my_test_b : 3213889832
my_struct->my_struct_a: 3213889836
my_struct->my_struct_b: 3213889844
my_struct->my_struct_c: 3213889848
//CYGWIN_NT-6.1 motadou-PC 1.7.20(0.266/5/3) 2013-06-07 11:11 i686 Cygwin
sizeof(char) = 1
sizeof(short) = 2
sizeof(int) = 4
sizeof(long) = 4
sizeof(float) = 4
sizeof(double) = 8
sizeof(long long) = 8
sizeof(long double) = 12
exapmle-1: sizeof(my_struct) = 16
my_struct->a: 2272336
my_struct->b: 2272340
exapmle-2: sizeof(my_struct) = 14
my_struct->a: 2272322
my_struct->b: 2272324
exapmle-3: sizeof(my_struct) = 24
my_struct->a: 2272296
my_struct->b: 2272304
my_struct->c: 2272312
example-4: sizeof(my_struct) = 20
my_struct->a: 2272276
my_struct->b: 2272288
my_struct->c: 2272292
example-5: sizeof(my_struct) = 24
my_struct->my_test_a : 2272248
my_struct->my_test_b : 2272252
my_struct->my_struct_a: 2272256
my_struct->my_struct_b: 2272264
my_struct->my_struct_c: 2272268
