SVG之Path路径详解(二)，全面解析贝塞尔曲线

前言

如果没看过上一篇文章，可以点击链接前往观看，循序渐进，体验更佳

在进入正题前，先温习一下svg的坐标系，x轴为水平向右，y轴为垂直向下

在前一篇文章中，我们已经了解了d属性的M、L、H、V、A命令，接下来，将继续了解剩下命令

d属性详解

主要定义了路径的路径数据，由描述路径的一系列命令数据组成

命令数据主要由命令及命令参数组成，多个命令参数之间可用空格或逗号(英文逗号)隔开

Q

该命令用于画二次贝塞尔曲线

Q | q后可跟4个参数：

1. x1：控制点横坐标位置
2. y1：控制点纵坐标位置
3. x：终点横坐标位置
4. y：终点纵坐标位置

四个参数两两一组，表示两组坐标，分别表示控制点坐标和终点坐标

一条二次贝塞尔曲线其实就是由起点、控制点和终点三点经过某种规律运算决定的，其中，起点由上一次绘制的结束点决定

其数学公式为：\(B(t)=(1-t)^2P\alpha +2t(1-t)P\beta +t^2P\gamma ，t\in [0,1]\)

本质上，是一系列点的集合

如下是一条二次贝塞尔曲线的绘制过程动画：

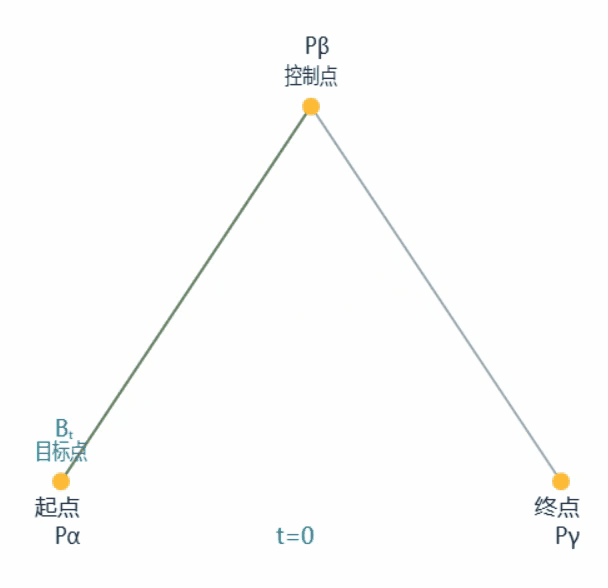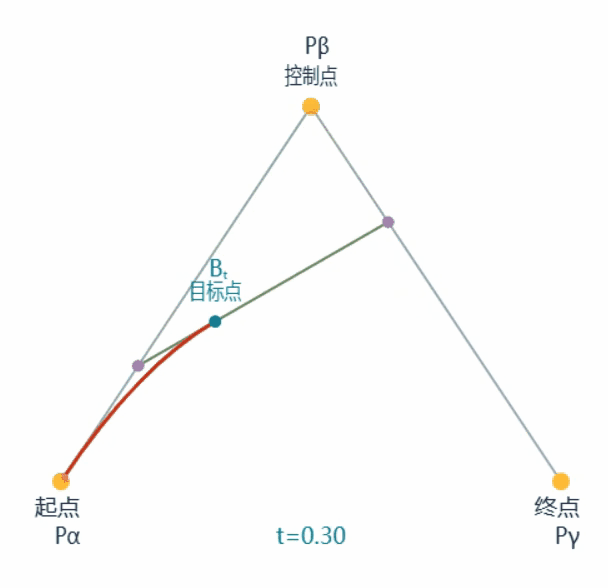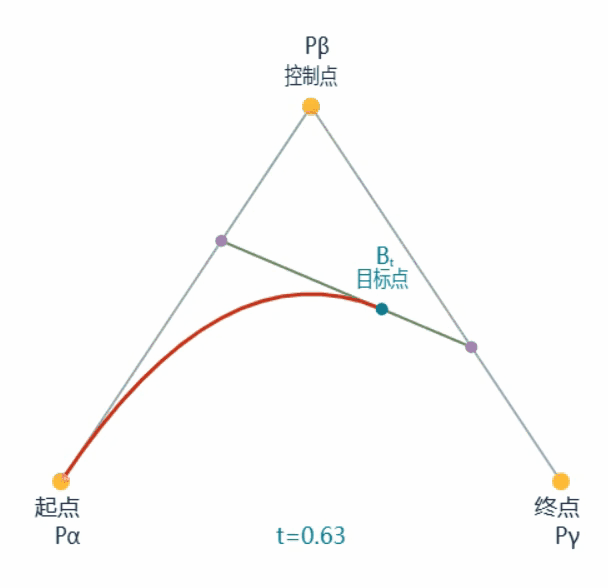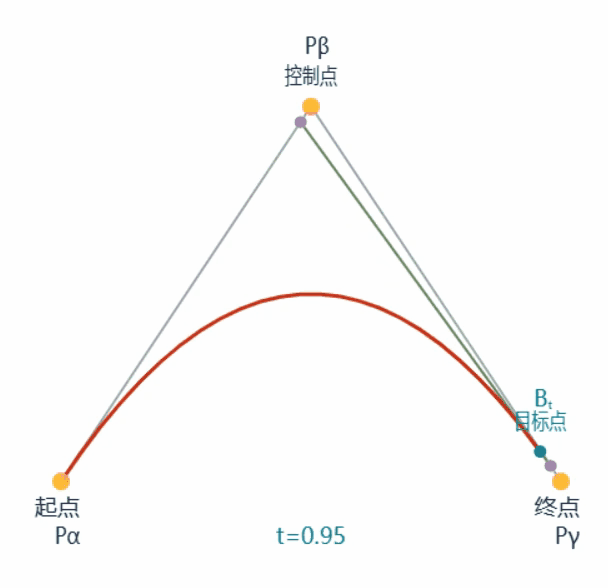
接下来提取其中一帧进行标注分析，如下

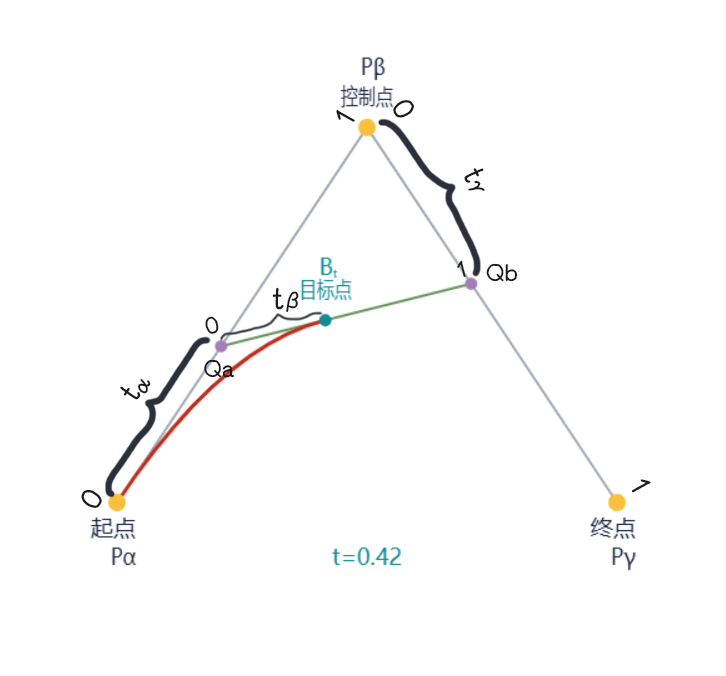
一条贝塞尔曲线由如图所示的一系列目标点B_t组成

目标点B_t又由Q_a和Q_b两点决定，其为两点连线的$\frac{t}{1} \(**处的点，其中**\)t\in [0,1]$

Q_a由起点与控制点决定，Q_b由控制点与终点决定，均为两点连线的$\frac{t}{1} $处的点

故可总结得，贝塞尔曲线的绘制过程为：

• 在\(t\in [0,1]\)中，每次取相邻两点连线的\(\frac{t}{1}\)处作为新的控制点

• 得出的新控制点继续取相邻两点连线的\(\frac{t}{1}\)处作为接下来的新控制点

• 以此递归，最终得出唯一的一个新控制点，即为组成贝塞尔曲线的点

起点与终点不之间不需要连线计算

该流程也适用于高阶贝塞尔曲线

用二次贝塞尔曲线论证，三个点经过一次运算即可得出两个新控制点，用新控制点再进行一次运算即可得出唯一的控制点，算出每个\(t\in [0,1]\)下唯一的控制点，其集合成的线即为二阶贝塞尔曲线

当然，以上只是为了帮助认识贝塞尔曲线的生成过程，知其然，也知其所以然，如不想了解也是可以正常使用贝塞尔曲线的

言归正传，以下给出几条命令的示例：

• <path M100 450 Q300 150 500 450 />
• <path M100 450 Q240 200 500 450 />

如想知道命令长啥样，可自行在svg文件内运行查看

T

该命令用于画平滑二次贝塞尔曲线

T | t后可跟2个参数：

1. x：终点横坐标位置
2. y：终点纵坐标位置

其实，该命令本质上也是用于画二次贝塞尔曲线，可以算是Q命令的简化版

只需要一个终点坐标即可生成曲线，但其实际上依旧由起点、控制点和终点三点生成，其中，控制点由上一次绘制的控制点关于其终点中心对称生成

故，T命令只能接在Q或T命令后使用，如单独出现或接于其它命令后出现，控制点会与其起点一致，绘制的效果会是一条直线

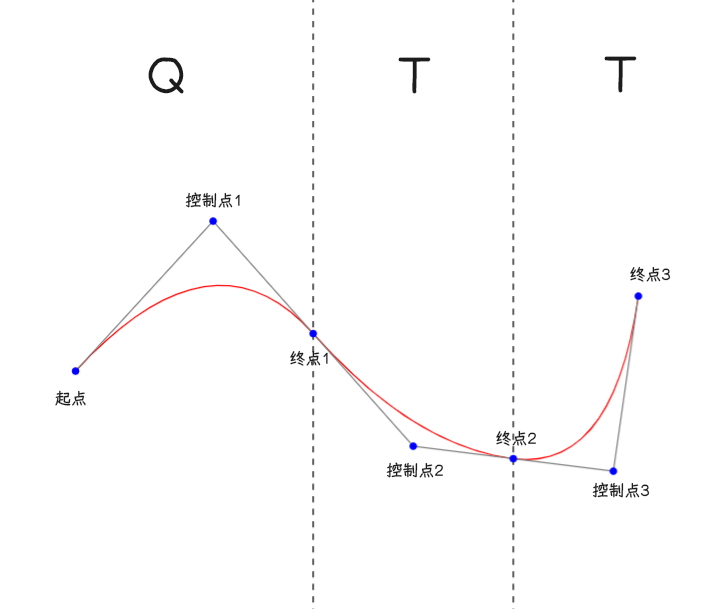
上图是一条曲线路径的示例图，由一次Q和两次T命令组成，其中T命令只需给出终点坐标即可，控制点2由控制点1绕终点1中心对称生成，控制点3由控制点2绕终点2中心对称生成

例：<path d="M50 300 Q 160 180 240 270 T400 370 T500 240" fill="none" stroke="red" />

C

该命令用于画三次贝塞尔曲线

C | c后可跟6个参数：

1. x1：控制点1横坐标位置
2. y1：控制点1纵坐标位置
3. x2：控制点2横坐标位置
4. y2：控制点2纵坐标位置
5. x：终点横坐标位置
6. y：终点纵坐标位置

三次贝塞尔曲线比二次贝塞尔曲线多一个控制点控制，故有6个参数

即其由起点、控制点1、控制点2和终点决定生成，生成方式与上方二次贝塞尔曲线讲的方式类似

数学公式为：\(B(t)=(1-t)^3P\alpha +3t(1-t)^2P\beta +3t^2(1-t)P\gamma +t^3P\delta ，t\in [0,1]\)

以下是一条普通三次贝塞尔曲线的生成过程动画：

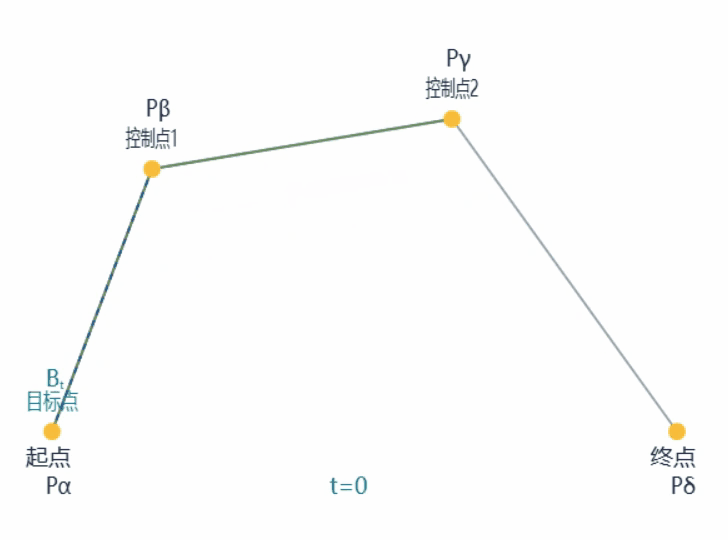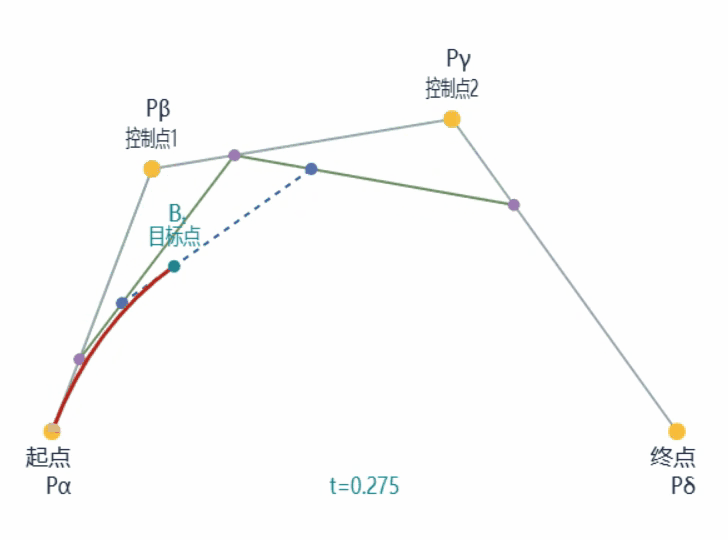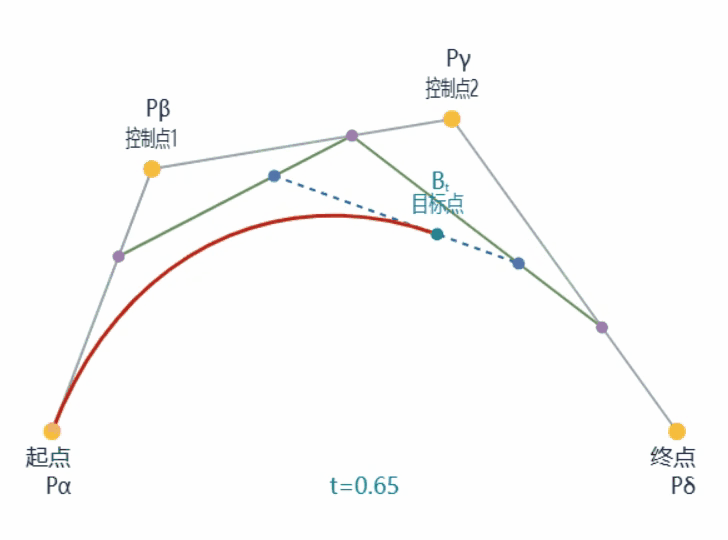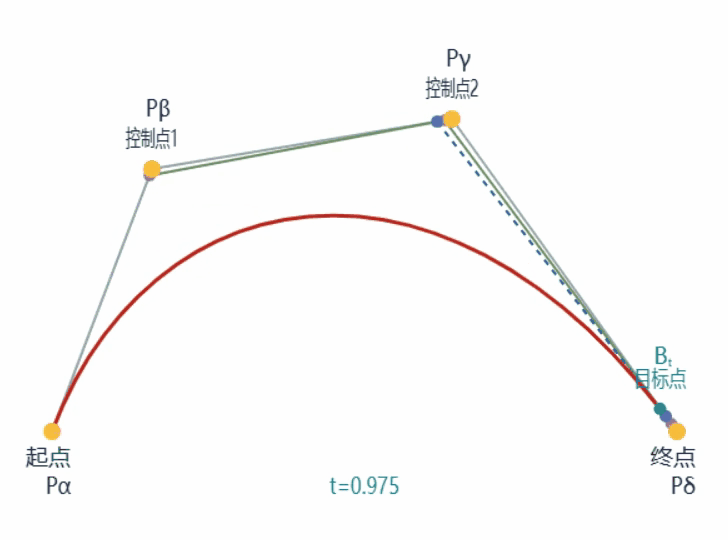
具体的描述不再赘述

S

该命令用于画平滑三次贝塞尔曲线

S | s后可跟4个参数：

1. x1：控制点2横坐标位置
2. y1：控制点2纵坐标位置
3. x：终点横坐标位置
4. y：终点纵坐标位置

其为C命令的简化版，只需指定一个控制点2和终点坐标即可

但其本质依旧是画三次贝塞尔曲线，实际上还是由起点、控制点1、控制点2和终点决定生成，其中，控制点1由上一次绘制的控制点关于其终点中心对称生成(即根据前一条命令的控制点2关于前一条命令的终点中心对称决定)

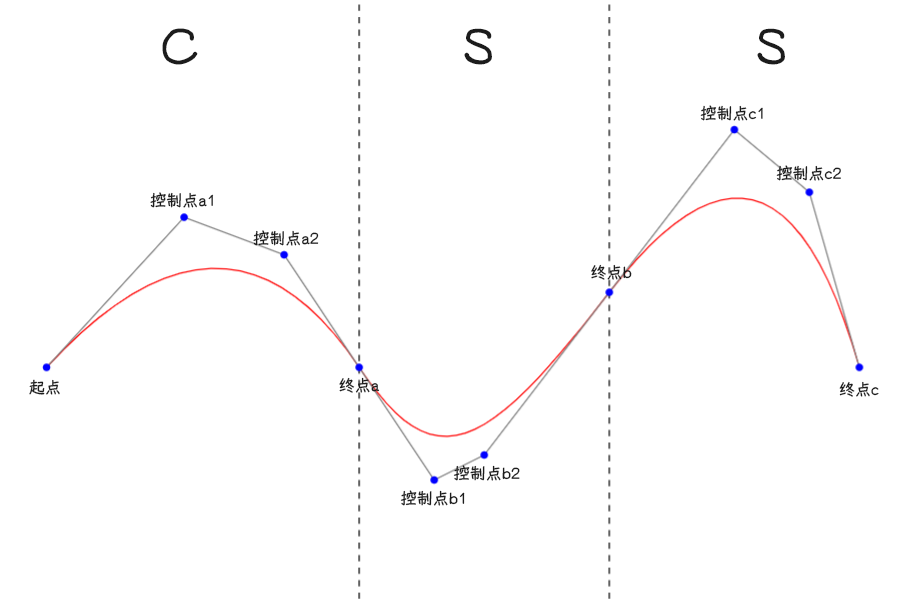
上图是一条曲线路径的示例图，由一次C和两次S命令组成，其中S命令只需给出控制点2和终点坐标即可，控制点b1由控制点a2绕终点a中心对称生成，控制点c1由控制点b2绕终点b中心对称生成

例：<path d="M50 300 C 160 180 240 210 300 300 S400 370 500 240 S660 160 700 300" fill="none" stroke="red" />

Z

该命令用于闭合路径，大小写字母均可，后面不需跟参数

命令会从当前位置到起点画一条直线闭合整个path

一般放在d属性命令数据的最后

名词解读

绝对： 指数值针对坐标系绝对

相对： 指数值针对上一点相对

对于d属性的命令，通常有大写字母和小写字母两种，大写表绝对，小写表相对

贝塞尔曲线： 是一种数学曲线，它拥有 灵活、平滑、可编辑 的特点，十分适合描述曲面形状、处理图形变形、模拟运动轨迹等场景