e网通物理必修一学习笔记

目录

• 匀变速直线运动规律总结课
  • 相对运动
    • 第一题
    • 第二题
    • 第三题
    • 第四题
    • 第五题
  • 综合习题精讲
    • 第一题
    • 第二题
    • 第三题
• 平抛运动和曲线运动概念
  • 曲线运动认识
  • 运动的合成与分解
    • 曲线运动合外力与速度的关系
    • 各种运动的判断
    • 过河问题
  • 探究平抛运动
  • 平抛运动的规律(习题）
    • 第1题
    • 第2题
    • 第3题
    • 第4题
    • 第5题
    • 第6题
    • 第7题

随看随补qwq，从相对运动开始写，之前的之后从头开始再看一遍 补充

后记，感觉写起来有点慢 = =，之后写的可能没那么详细，或许会咕咕。

---

匀变速直线运动规律总结课

相对运动

甲乙两物体如下图运动

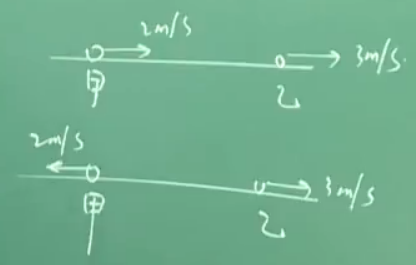
图一 ： 我们可以看作乙相对于甲在向右以$ 1m/s$运动，即甲看到乙向右\(1m/s\)的速度运动
同样我们可以看作甲相对于乙在向左以$ 1m/s$运动，即乙看到甲向左\(1m/s\)的速度运动
图二 ： 我们可以看作乙相对于甲在向右以$ 5m/s$运动，即甲看到乙向右\(5m/s\)的速度运动
同样我们可以看作甲相对于乙在向左以$ 5m/s$运动，即乙看到甲向左\(5m/s\)的速度运动
总结，乙相对甲怎么运动，就是甲看到乙怎么运动。
当存在加速度的时候同样成立

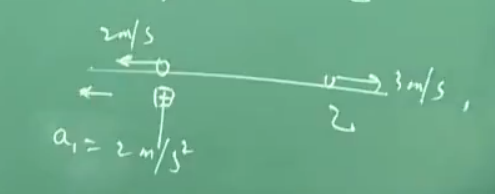
如图，甲有向左的加速度 $ a_1 $，即甲相对于乙有向左的加速度，乙相对于甲有向右的加速度，和上边类似。

第一题

\(solution\)

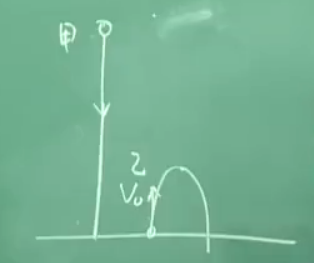
如图
甲物体有向下的加速度\(g\)，乙物体有向上的初速度\(v_0\),向下的加速度\(g\)。
根据相对运动，可以看作乙物体对于甲物体向上运动，也就是甲物体看到乙物体向上运动，选择\(A\)项。

第二题

\(solution\)
板书

题目要求相遇几次，根据加速度的大小分成三种情况讨论

• 若\(a_1== a_2\)，即甲乙加速度相同，也就是乙相对于甲做\(v_0\)的匀速直线运动，相遇一次。
• 若\(a_2>a_1\)，即乙相对于甲做\(a_2-a_1\)的匀加速运动，必然只会相遇一次。
• 若\(a_2<a_1\)，即乙相对于甲做\(a_1-a_2\)的运减速运动，显然有可能相遇一次，两次，甚至没有相遇。
• 答案 \(A\)。

第三题

\(solution\)
相对加速度为\(3a\)，相对位移为$s - L $

由\(s == (v^2 - v_0^2)/ 2a\)，得出结果
图

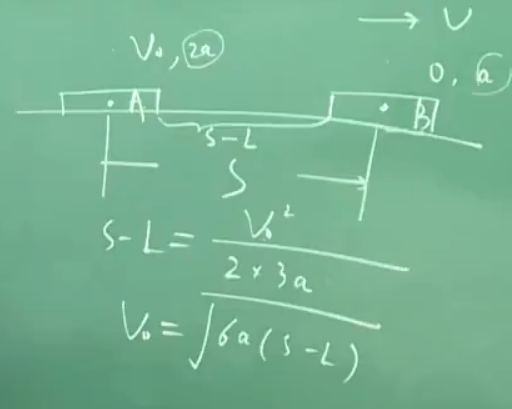
第四题

\(solution\)
分析全过程，甲相对于乙有向右的\(20m/s\)的加速度，由\(s == (v^2 - v_0^2)/ 2a\)，得出结果

太快了！！

第五题

和前边类似，不多说了

综合习题精讲

第一题

\(solution\)
\(Δt\) , 实际上是A球上升，后至抛出位置所用的时间。
\(Δt=2v_0/g\)，发现与\(h\)无关。
选B

第二题

列出\(Δt\) 的表达式
\(Δt ==\sqrt{\frac{2}{g}}*(\sqrt{h}-\sqrt{h-L})\)
由于被减数减数都在变大，无法判断Δt的变化。
1 化简

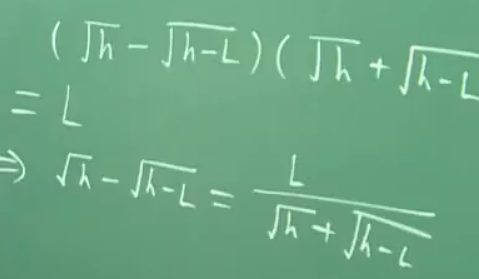
由上述式子得到\(Δt ==\sqrt{\frac{2}{g}}*\frac{L}{(\sqrt{h}+\sqrt{h-L})}\)
\(h\)变大，分母变小，\(Δt\)变小
2
当把小球拿到\(6\)亿楼时，\(L\)相对与\(h\)可以忽略不记，
也就是此时\(Δt\)为\(0\)。
所以选A

第三题

小球从出发点再回到出发点需要\(1.2s\)
看图一目了然
选\(C\)

平抛运动和曲线运动概念

曲线运动认识

• 曲线运动的特点：
  • 一切曲运动都需要向心力
  • 曲线运动的方向：延运动的切线方向，火星飞出，雨伞转雨等。曲线运动的方向时刻在变化。
  • 曲线运动的向心力指向运动的凹侧。
  • 曲线运动是变速运动，具有加速度，即向心加速度。
• 曲线运动与直线运动的区别
  • \(F(a) // v\):直线运动
    • \(a\)恒定，匀变速
    • \(a\)变化，变加速
  • \(F(a) 不// v\)：曲线运动
    • \(a\)恒定，匀变速（平抛运动）
    • $ a$变化，变加速（匀速圆周运动）
• 为什么有些物体做直线运动，有些物体会做曲线运动？
  • 当力与速度方向平行，即加速度与速度反向平行时，物体做直线运动；反之做曲线运动。
• 物体做曲线运动的条件：
  • 当物体所受的合外力方向(向心力)跟它的速度方向不在同一直线上时，物体做曲线运动。
• 生活实例
  • 飞机扔炸弹，炸弹有向前的速度v，受到竖直向下的重力mg，即为平抛运动。
  • 盘山公路和火车轨道的特点，内侧低，外侧高。

运动的合成与分解

并不会讲很多运动和分解= =

曲线运动合外力与速度的关系

• 合外力指向运动轨迹的凹侧。
• 合力沿切线方向的分力改变速度的大小，沿径向的分力改变速度的方向，即向心加速度。
• 当合外力方向与速度方向为锐角时，物体运动速率将增大。
• 当合外力方向与速度方向为锐角时，物体运动速率将减小。
• 当合外力方向与速度方向垂直时，物体运动速率不变。
• 物体运动的轨迹在合外力与速度方向之间。
  题目
  
  分析
  合力方向指向凹侧，排除AD；
  再由于速度逐渐减小，也就是合力方向与速度方向为钝角，排除B；

各种运动的判断

匀不匀看加速度，拐不拐看角度

过河问题

探究平抛运动

• 概念：以一定的初速度将物体抛出，在空气阻力可以忽略的情况下，在只受重力作用的情况下物体所做的运动。

• 平抛运动可以分解为水平方向上的匀速直线运动与竖直方向上的自由裸体运动。
  如图

• 物体运动的时间t，由抛出时的高度h决定； h越高，t越长。物体运动的水平距离，由初速度和高度共同决定。

• 物体运动的水平速度，恒为\(v_0\)。竖直速度，为\(gt\)。

• 平抛运动任意一点的速度的方向延长线过水平位移的中点。(自己推一推吧)

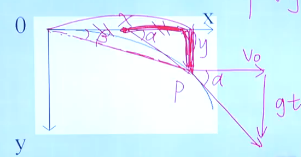
平抛运动的规律(习题）

• 关键 ：平抛分方向

第1题

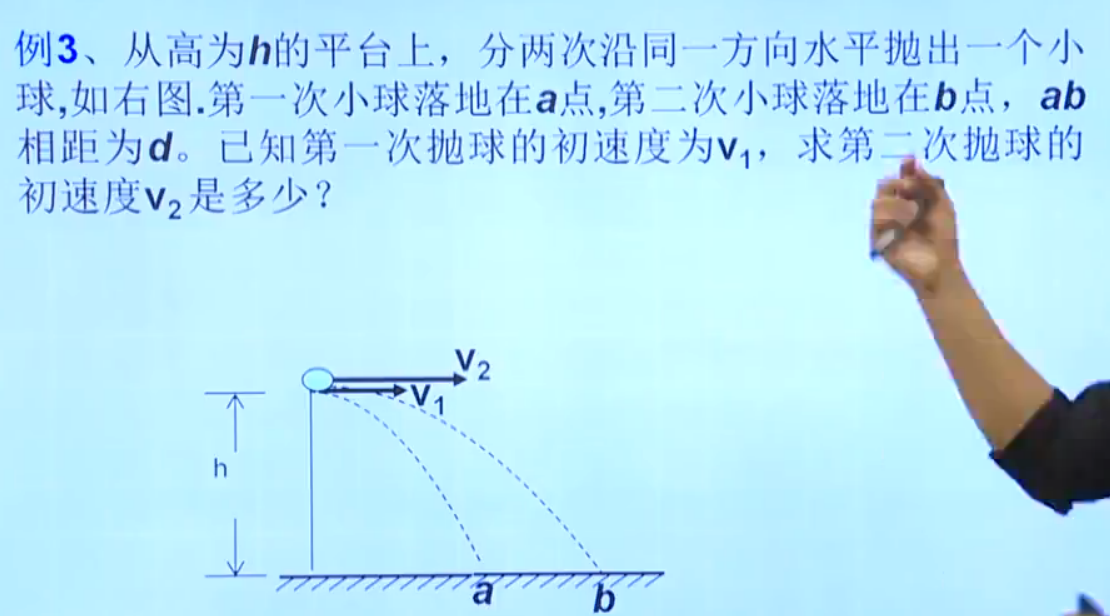
运动时间不变，根据水平距离列出方程。
\((v_1-v_2)*\sqrt\frac{2h}{g} == d\)
解\(v\)就完了。

第2题

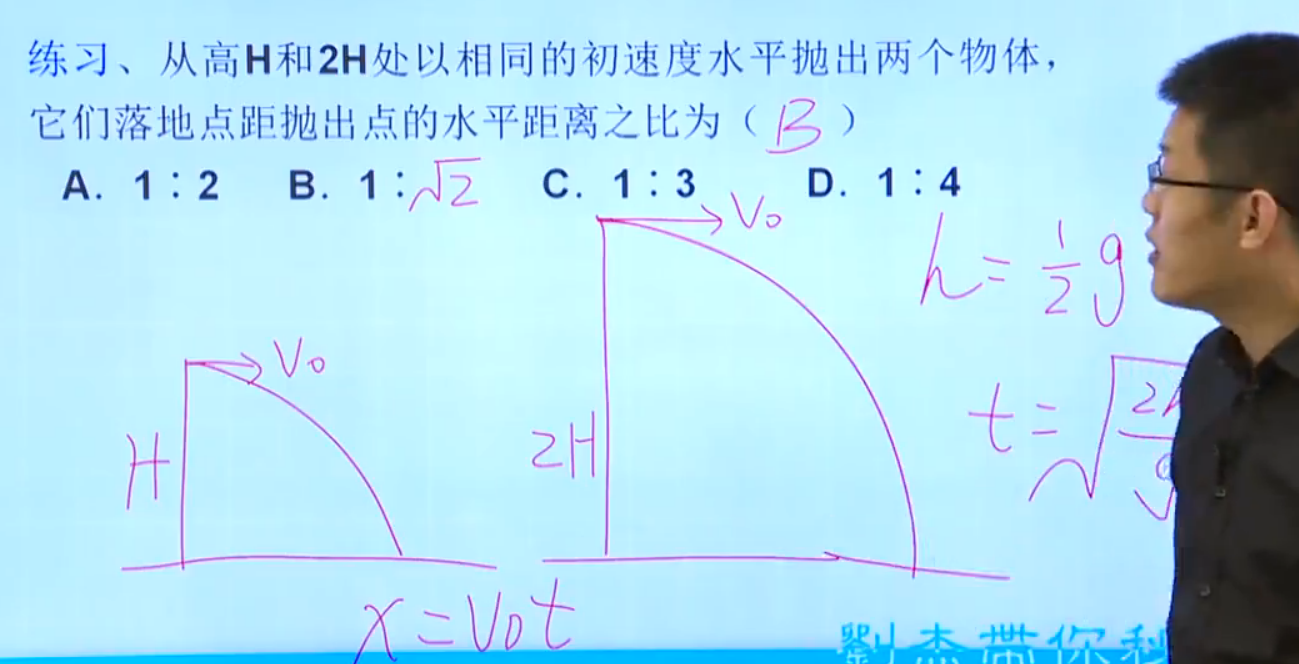
根据\(v_0\)不变，则距离之比等于时间之比
即B

第3题

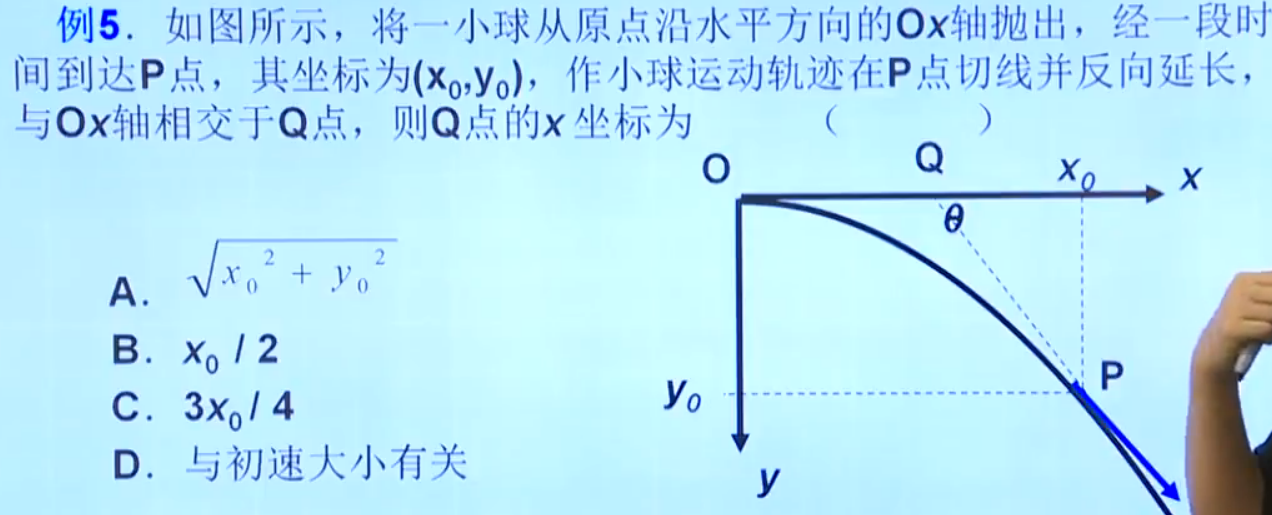
直接运用上边的结论，速度的方向延长线过中点，选B。

第4题

看选项
对于AB选项，雨滴飞出的方向应该是切线方向，A错；
对于CD选项，很明显C选项根据常识不可能正确。选D。
推一下D 选项
几何知识知道，圆的切线和半径是垂直的。
当雨滴沿切线飞出，落地点与伞中心的连线就是新圆的半径，同时构成了直角三角形。
运动时间\(t = \frac{2h}{g}\),角速度\(w\)，线速度为\(wR\)，则水平方向上的位移\(s=wRt\)。
原圆半径为R，根据毕达哥拉斯定理(雾)，得出新的半径，\(r = R\sqrt{1+\frac{2hw^2}{g}}\)。

第5题

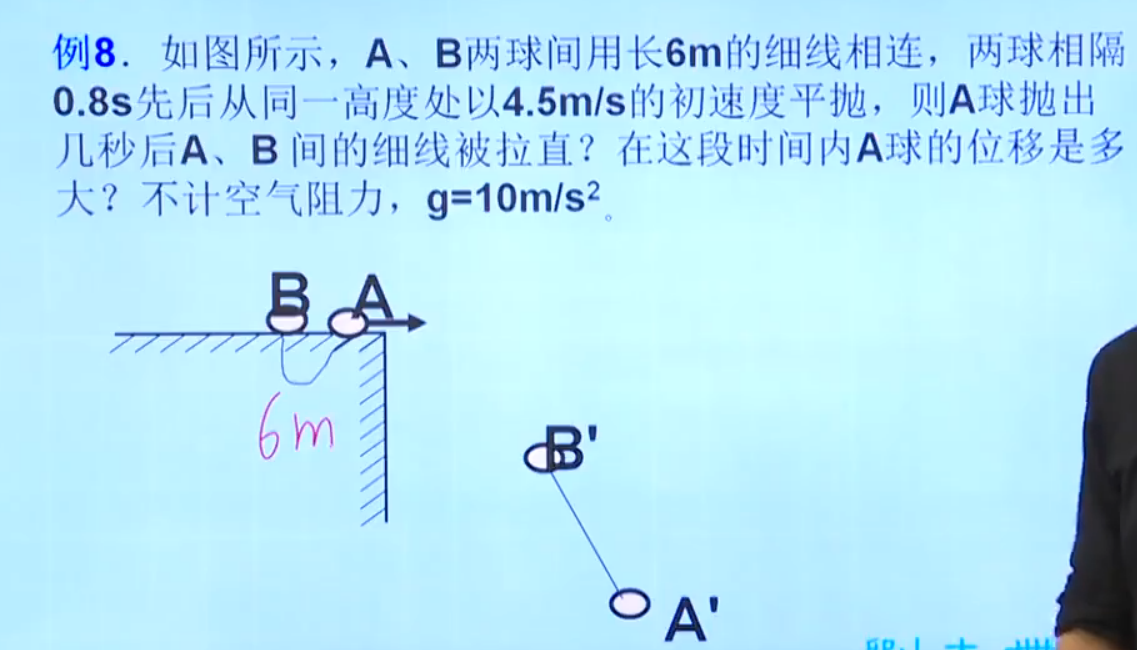
是否拉直，也就是说，绳子长度有没有达到\(6m\)。
先判断在\(B\)下落之前，绳子拉直没。
这种情况下，\(A\)的水平距离为\(3.6m\)，竖直距离为\(3.2m\),根据勾股定理得绳子的长短为\(26m\)左右,小于36，也就是绳子没有被拉直。
既然没有被拉直，就说明两个球之间不存在相互作用，可以看作是两个球不同时刻出发的平抛运动。
假设在t时刻绳子绷直，可得坐标$$A(v_0t,1/2gt^{2),B(v_0(t-0.8)，1/2g(t-0.8)}2 )$$

根据两点之间距离公式得出AB距离，与6m联立方程，解的t，进而解的\(s_a\)。

第6题

因为要求距斜面的最大距离，也就是物体在垂直与斜面方向上的距离。
平抛分方向，平抛分方向。
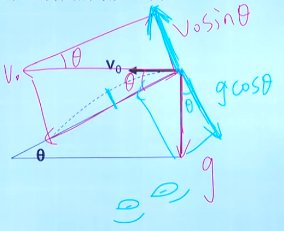
将水平的\(v_0\)分解为沿着斜面的速度和垂直与斜面的速度\(v_0sin~~0~~\)。
将重力加速度分解为垂直于斜面的加速度\(gcos~~0~~\).
见下图。
此时物体在垂直于斜面方向上做匀减速运动，当速度减到\(0\)的时候,距离最大。根据位移速度公式得出结果。

第7题

物体水平方向上没有速度的变化，竖直方向上做自由落体运动，
所以速度的改变量是相同的，方向也相同。