skkyk:点分治
由题开始==
例题:求在一棵有权树上,是否存在一条路径满足权值和为K
解法:以每个点为根一次,看在他的子树间是否存在两段,其和为K;O(==)
和例题一样,对于树上问题,求某些要求的路径(数量或者存在性等),
往往可以先对一条经过根节点的路径操作,
后再删去这个根,对他的子树们同样的操作
显然是一个分治过程
原理就是,一条路径,要么是由一个点经过根节点,与其他子树内的节点形成;
要么就是只在这棵子树内形成路径
大概图示意思(红绿为两条上述路径)
<
当我们的树比较平衡时,每个点被路径计算是$ logn $ 的,但是当树是一条链的时候,就退化成$ n^2 $ 了
为了避免这种情况,可以用树的重心代替,成为新的根。此时总复杂度为$ O (nlogn) 。$
原因就是,一棵树,怎么为根都还是一颗树,但是以重心为根的时候,这颗树是最好看的最平衡的
rt,将链按箭头提起来:
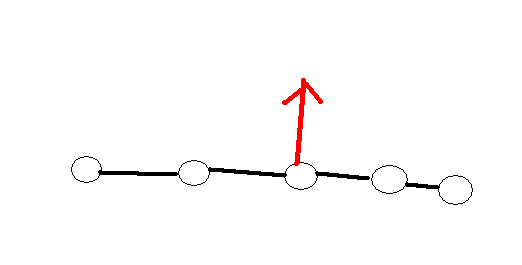
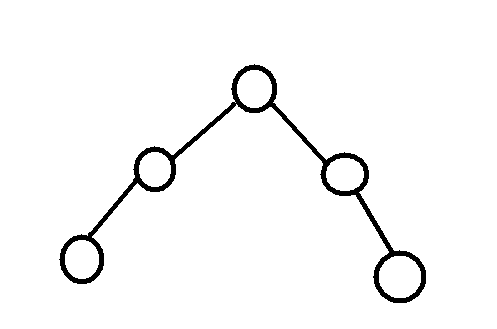
这看向去更像是一棵树
。
所以
总结一下
一棵树先确定他的重心,以重心为根,确定经过根节点的路径;再把根节点删掉,对于删掉他的子树们,按上述同样操作;
已证$ O(nlogn) $。
luogu模板题代码仅供参考,不解释。
#include<bits/stdc++.h>
using namespace std;
const int N = 1e4+50;
const int K = 1e7+50;
int n,m;
struct node{int next,to,dis;}edge[N<<1];
int head[N],cnt;
inline void add(int from,int to,int dis) {
edge[++cnt].to=to,edge[cnt].dis=dis,edge[cnt].next=head[from],head[from]=cnt;
}
int q[N],ans[N],maxp[N],size[N],visited[N],tmp[N],dis[N],judge[K];
int rt,sum,tot;
void getrt(int u,int f) {
size[u]=1,maxp[u]=0;
for(int i=head[u];i;i=edge[i].next) {
int v=edge[i].to;if(v==f||visited[v]) continue;
getrt(v,u);
size[u]+=size[v];maxp[u]=max(maxp[u],size[v]);
}
maxp[u]=max(maxp[u],sum-maxp[u]);
if(maxp[u]<maxp[rt]) rt=u;//要求最大的最小
}
void getdis(int u,int f) {
tmp[++tot]=dis[u];
for(int i=head[u];i;i=edge[i].next) {
int v=edge[i].to;if(v==f||visited[v]) continue;
dis[v]=dis[u]+edge[i].dis; getdis(v,u);
}
}
queue<int> que;
void solve(int u) {
for(int i=head[u];i;i=edge[i].next) {
int v=edge[i].to;if(visited[v]) continue;
dis[v]=edge[i].dis;
tot=0;getdis(v,u);
for(int j=1;j<=tot;j++)
for(int k=1;k<=m;k++)
if(q[k]>=tmp[j])
ans[k]|=judge[q[k]-tmp[j]];
for(int j=1;j<=tot;j++) que.push(tmp[j]),judge[tmp[j]]=1;
}
while(!que.empty()) judge[que.front()]=0,que.pop();//数组过大,memset超时
}
void divide(int u) {
judge[0]=visited[u]=1;solve(u);
for(int i=head[u];i;i=edge[i].next) {
int v=edge[i].to;if(visited[v]) continue;
maxp[rt=0]=sum=size[v];
getrt(v,0),getrt(rt,0);
divide(rt);
}
}
int main() {
cin>>n>>m;
for(int i=1;i<n;i++) { int a,b,c;scanf("%d%d%d",&a,&b,&c);add(a,b,c),add(b,a,c);}
for(int i=1;i<=m;i++) scanf("%d",q+i);
maxp[rt=0]=sum=n;//初始化
getrt(1,0),getrt(rt,0);//找重心
divide(rt);//点分治
for(int i=1;i<=m;i++) if(ans[i]) puts("AYE");else puts("NAY");
return 0;
}
我就是我不一样的验货



