1.内容小结
依据惯例，还是先回顾一下学过的，可能会有新的体会。
- 树和二叉树
- 二叉树的遍历
- 哈夫曼树
树和二叉树：
树是使用了递归定义的数据结构，是一个n(n>=0)个结点的有限集，递归定义简单理解就是——树的子树还是树（注意：空树也被划分为树）；
二叉树是每个结点最多有两个子树的树。它有五种基本形态：空二叉树、仅有根节点的二叉树、左子树均为空的二叉树、右子树为空的二叉树、左右子树均非空的二叉树。五种基本形态构成了所有形态不一的树。
二叉树的一些性质:
- 二叉树第i层上的结点数目最多为2 ^ (i-1) ( i>=1)；
- 深度为k的二叉树至多有2^k - 1个结点（k>=1)；
- 在任意一棵二叉树中，若终端结点的个数为n0，度为2的结点数为n2，则n0=n2+1；
- 包含n个结点的二叉树的高度至少为(log2n)+1（适用于完全二叉树）；
这些基本的性质可能很少在编程时用到，但一些关于树的面试选择题却经常涉及，记住的话能省去不少推算时间，还是挺重要的。
二叉树的遍历：
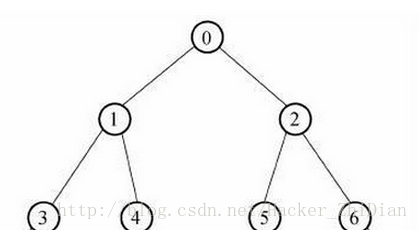
二叉树的遍历可分为四种，即先序、中序、后序遍历和层序遍历。
- 先序：根节点 –> 左子树 –> 右子树。 上图中二叉树的前序遍历结果为：0 -> 1 -> 3 -> 4 -> 2 -> 5 -> 6
- 中序：左子树 –> 根节点 –> 右子树。 上图中二叉树的中序遍历结果为：3 -> 1 -> 4 -> 0 -> 5 -> 2 -> 6
- 后序：左子树 –> 右子树 –> 根节点。 上图中二叉树的后序遍历结果为：3 -> 4 -> 1 -> 5 -> 6 -> 2 -> 0
- 层序：从最顶层的节点开始，从左往右，从上往下，一层一层遍历，直到所有节点都遍历完成 。上图中二叉树的层序遍历结果为：0 -> 1 -> 2 -> 3 -> 4 -> 5 -> 6
前三种容易想到，也好理解，因为树本身就是递归定义的，运用递归算法就能得到相应的遍历次序（也可以借助辅助栈实现将该递归算法改为非递归算法，但本质上还是用到了递归思想）
层序遍历就有点取巧了，需要借助队列这种数据结构来完成。借用队列先进先出的特点，将一棵二叉树的根节点加入队尾，然后循环出队，每次读取队头元素输出并且将队头元素出队，然后将这个输出的元素节点的的左右子树依次加入队尾，重复循环，直到队列为空，完成整个遍历。如本章list leaves和合作打代码的遍历函数，就是很经典的一种结合队列的层序遍历。
哈夫曼树：
哈夫曼是一类带权路径长度最短的树，通过树所有节点的带权路径长度之和（wpl)可以求得。
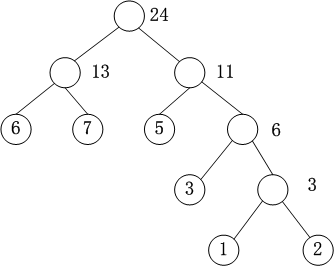
通过一个例子来回顾：由权值为3,6,7,2,5,1的叶子结点生成一棵哈夫曼树，它的带权路径长度为？
wpl = 7*2 + 6*2 + 5*2 + 3*3 + 2*4 + 1*4 = 57.
写到这儿卡住挺久，似乎关于哈夫曼树的了解就只停留在会手工算wpl，还没去真正地代码实现，哈夫曼树真正的用途（编码译码）也没去了解，羞愧....
2.一些收获：
- check[]数组的应用判断根节点；
- 树的同构一题对多条件递归的深入理解；
- 数组、链表、栈和队列的巧妙结合；
- 小组合作暴露了平时没有考虑数组越界的问题；
- .....
