239. Sliding Window Maximum

一、题目

　　1、审题

　　

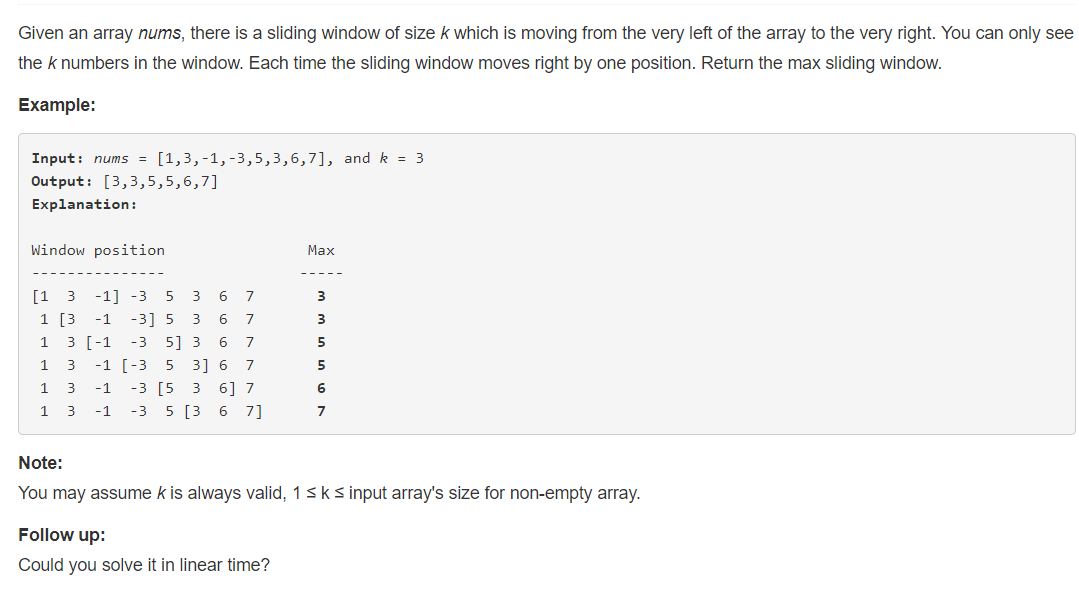
　　2、分析

　　　　给出一个整形数组，一个窗口大小 k，此窗口每次包含 k 个连续元素，依次向后移动，将每次窗口中的最大元素进行记录。

 

二、解答

　　1、思路

　　　　方法一、

　　　　　　采用双端队列 Deque 存储每次窗口中最大元素的下标 i，且队列中存储的下标是依次增大的。

　　　　　　①、循环判断队列中元素值 < i - k + 1，则元素出队列。

　　　　　　②、循环判断，队列后部分的元素下标对应的元素值是否小于当前遍历的元素的值，若是，则从后部依次出队。 // 保证了下标对应的元素的值是递增的。

　　　　　　③、当前元素下标入队。

　　　　　　解释不是太清楚，具体摘自：

　　　　　　　　https://leetcode.com/problems/sliding-window-maximum/discuss/65881/O(n)-solution-in-Java-with-two-simple-pass-in-the-array

    public int[] maxSlidingWindow2(int[] nums, int k) {
        
        if(nums == null || k <= 0)
            return new int[0];
        
        int n = nums.length;
        int[] r = new int[n - k + 1];
        int ri = 0;
        
        Deque<Integer> q = new ArrayDeque<>(); // store index
        for(int i = 0; i < n; i++) {
            // remove numbers out of range k
            while(!q.isEmpty() && q.peek() < i - k  + 1)
                q.poll();
            
            // remove smaller numbers in k range as they are useless
            while(!q.isEmpty() && nums[ q.peekLast()] <= nums[i])
                q.pollLast();
            
            q.offer(i);
            if(i >= k - 1)
                r[ri++] = nums[q.peek()];
        }
        return r;
    }

 

　　方法二、

　　　　采用两个整形数组 leftWindow、rightWindow。

　　　　将数组 nums 从前向后分成 n 个窗口，其中每份含有 k 个元素（最后一份可能小于 k）。

　　　　leftWindow 存储从左向右遍历元素，当前窗口的最大值。rightWindow存储从右向左遍历元素，当前窗口的最大值。

　　　　最终所求的窗口最大值即为： re[i] = Math.max(leftWindow(i), rightWindow[i - k + 1]) , 其中 leftWindow 与 rightWindow 分别是当前窗口的 尾部和头部。

    public int[] maxSlidingWindow22(int[] nums, int k) {
        
        if(nums == null || k <= 0)
            return new int[0];
        
        int n = nums.length;
        int[] leftWindow = new int[n];
        leftWindow[0] = nums[0];
        int[] rightWindow = new int[n];
        rightWindow[n - 1] = nums[n - 1];
        for (int i = 1, j = n - 2; i < n; i++, j--) {
            leftWindow[i] = (i % k == 0 ? nums[i] : Math.max(nums[i], leftWindow[i-1]));
            rightWindow[j] = (j % k == 0 ? nums[j] : Math.max(nums[j], rightWindow[j + 1]));
        }

        int[] re = new int[n - k + 1];
        for (int i = k - 1, j = 0; i < n; j++, i++) 
            re[j] = Math.max(leftWindow[i], rightWindow[j]);
        return re;
    }