207. Course Schedule

一、题目

　　1、审题

　　

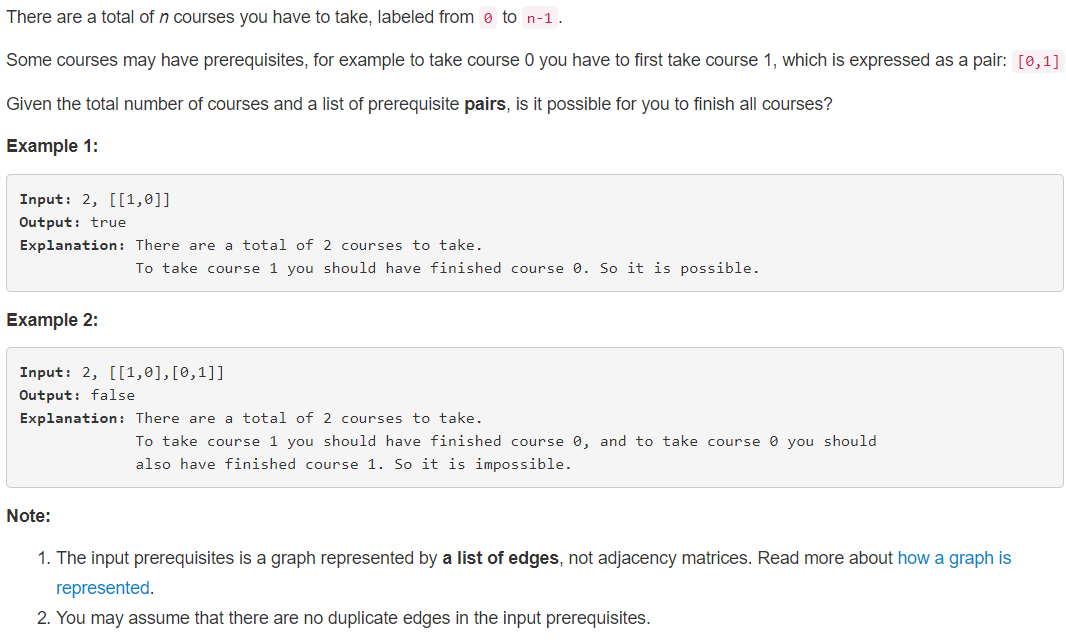
　　2、分析

　　　　给出顶点数、指向当前顶点的前驱顶点，判断当前顶点组成的图是否是一个有向无环图。

 

二、解答

　　1、思路：

　　　　方法一、

　　　　　　采用拓扑排序

　　　　　　①、定义数组 matrix[][] 存储从 i 指向 j 的边，curArr[] 存储指向当前顶点的边数。并初始化这两个数组；

　　　　　　②、将没有前驱的顶点存入队列中，依次出列；

　　　　　　③、将出列的顶点为起始的边依次去除，即将 curArr[i] 值 -1；若 curArr[i] == 0，则 i 入队列；

　　　　　　④、最终队列为空时，若总共入队的元素个数与顶点个数相等，则为有向无环图，否则，为有环图。

    public boolean canFinish2(int numCourses, int[][] prerequisites) {
        
        int[][] matrix = new int[numCourses][numCourses];    // 存储边
        int[] curArr = new int[numCourses];            // curArr[m] = n: 有 n 个指针指向 m 
        
        for (int i = 0; i < prerequisites.length; i++) {
            int pre = prerequisites[i][1];
            int cur = prerequisites[i][0];
            
            if(matrix[pre][cur] == 0)
                curArr[cur] = 1;
            matrix[pre][cur] = 1;
        }
        
        Queue<Integer> queue = new LinkedList<>();
        for (int i = 0; i < numCourses; i++) {
            if(curArr[i] == 0)
                queue.offer(i);
        }
        
        int count = 0;
        while(!queue.isEmpty()) {
            count++;
            int course = queue.poll();
            for (int i = 0; i < numCourses; i++) {
                if(matrix[course][i] != 0 && --curArr[i] == 0)
                    queue.offer(i);
            }
        }
        return count == numCourses;
    }

 

　　方法二、

　　　　采用 DFS

　　　　①、首先构造图，用 Map 存储，Key 为顶点，value 为直接前驱顶点；

　　　　②、往前驱顶点进行深度遍历图中每个顶点，判断是否该顶点重复出现，若是，返回 false；

　　　　③、遍历完途中的所有顶点，返回 true；

    public boolean canFinish(int numCourses, int[][] prerequisites) {
        if(prerequisites == null)
            return false;
        
        // key: 当前顶点， value： 所有直接前驱顶点
        HashMap<Integer, List<Integer>> grap = new HashMap<>();
        for(int[] curPair: prerequisites) {
            List<Integer> match = grap.get(curPair[0]);
            if(match == null) {
                match = new ArrayList<Integer>();
                match.add(curPair[1]);
                grap.put(curPair[0], match);
            }
            else {
                match.add(curPair[1]);
            }
        }
        
        HashSet<Integer> prevRoots = new HashSet<>();
        for(Integer curRoot: grap.keySet()) {
            boolean[] hasCircle = new boolean[1];
            DFS(prevRoots, curRoot, grap, hasCircle);
            if(hasCircle[0])
                return false;
        }
        return true;
    }
    
    private void DFS(HashSet<Integer> prevRoots, Integer start,
            HashMap<Integer, List<Integer>> grap, boolean[] hasCircle) {
        
        if(hasCircle[0])    // 跳出条件
            return;
        else if(prevRoots.contains(start)) {
            hasCircle[0] = true;
            return;
        }
        
        prevRoots.add(start);
        List<Integer> match = grap.get(start);
        if(match != null) {
            for(Integer newStart: match)
                DFS(prevRoots, newStart, grap, hasCircle);
        }
        prevRoots.remove(start);
    }