162. Find Peak Element

一、题目

　　1、审题

　　

　　2、分析

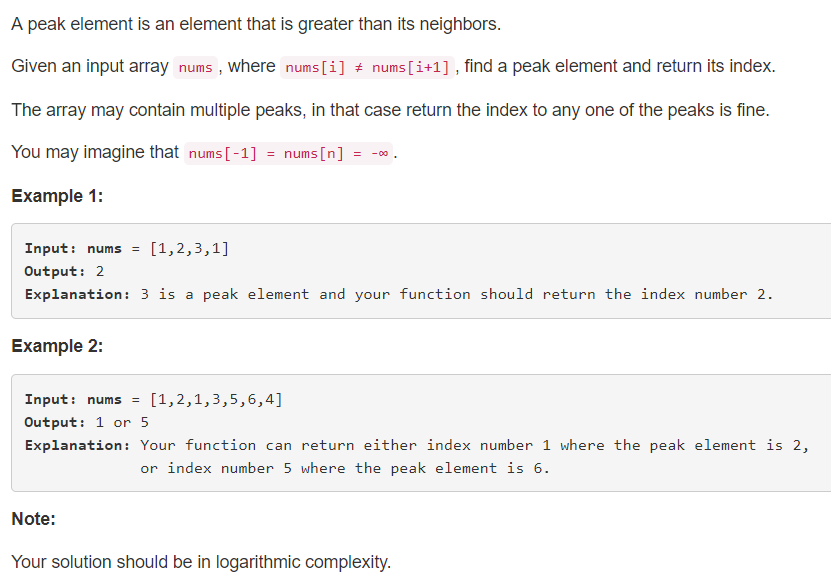
　　　　给出一个整形数组，输出比左右元素值大的数值的下标。若左边或右边没有元素，则视为左或右边 为负无穷大。

 

二、解答

　　1、思路：

　　　　方法一、

　　　　　　直接顺序遍历数组，判断是否比左右元素值大。

    public int findPeakElement(int[] nums) {
     
        int len = nums.length;
        
        // 处理长度为 1 的数组
        if(len == 1)
            return nums[0];
        // 处理长度大于 2 的数组的第一个元素
        if(len >= 2 && nums[0] > nums[1])
            return  0;
        // 处理长度大于 2 的数组的最后一个元素
        if(nums[len - 1] > nums[len - 2])
            return len - 1;
        
        // 处理有前后元素的数组元素
        for (int i = 1; i < len - 1; i++) {
            if(nums[i - 1] < nums[i] && nums[i] > nums[i + 1])
                return i;
        }
        
        return -1;
    }

 

　　方法二、

　　　　所求元素即为一个顶点。

　　　　其实不用专门判断比左边元素大。直接用 if 判断即可

    public int findPeakElement2(int[] nums) {
        
        for (int i = 1; i < nums.length; i++) {
            // i - 1 左边是更小的数，故只要判断 i - 1右边的数
            if(nums[i - 1] > nums[i])    
                return i - 1;
        }
        
        return nums.length - 1;
    }

 

　方法三、

　　　　采用二分法。找一个峰值点。

　　　　递归方式：

    public int findPeakElement(int[] nums) {
        return findPeakHelper(nums, 0, nums.length - 1);
    }
    
    private int findPeakHelper(int[] nums, int low, int high) {
        if(low == high)
            return low;
        
        int mid1 = low + ((high - low) >> 1);
        int mid2 = mid1 + 1;
        if(nums[mid1] > nums[mid2])
            return findPeakHelper(nums, low, mid1);
        else 
            return findPeakHelper(nums, mid2, high);
    }

　　　　

　　迭代方式：

    // Consider that each local maximum is one valid peak.
    public int findPeakElement3(int[] nums) {
        
        int low = 0;
        int high = nums.length - 1;
        
        while(low < high) {
            int mid1 = low + ((high - low) >> 1);
            int mid2 = mid1 + 1;
            if(nums[mid1] < nums[mid2])
                low = mid2;
            else
                high = mid1;
        }
        
        return low;
    }