140. Word Break II

一、题目

　　1、审题

　　2、分析

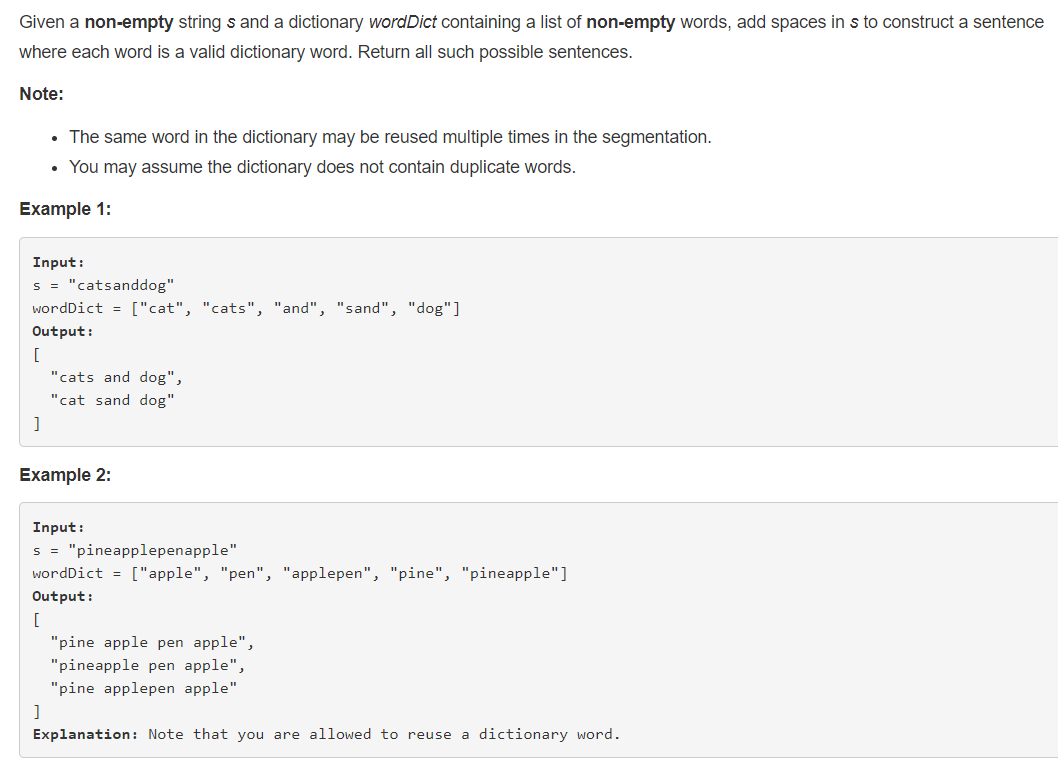
　　　　给出一个字符串，求其可以切割成字典List 中的元素的所有切法。

 

二、解答

　　1、思路：

　　　　方法一、

　　　　　　采用 DFS 方式。

　　　　　　从字典表中开始拿字符串与 S 的头部进行匹配，若匹配成功，则继续拿字典表在 S 的剩下的字符串进行匹配。直至 S 剩下的字符串为空，此时就找到一种切法。

　　　　　　最终返回所有切法的 List。

    public List<String> wordBreak23(String s, List<String> wordDict) {
        return DFS(s, wordDict, new HashMap<String, ArrayList<String>>());
    }
    
    private List<String> DFS(String s, List<String> wordDict,
            HashMap<String, ArrayList<String>> map) {

        if(map.containsKey(s))
            return map.get(s);
        
        ArrayList<String> res = new ArrayList<>();
        
        for(String word: wordDict) {    
            if(s.startsWith(word)) {    // 暴力尝试法
                String next = s.substring(word.length());
                if(next.length() == 0)
                    res.add(word);
                else { 
                    List<String> subList = DFS(next, wordDict, map);
                    for(String sub : subList)
                        res.add(word + " " + sub);
                }
            }
        }
        map.put(s, res);
        return res;
    }

　　

　　方法二、

　　　　采用 DP + DFS方式。

　　　　①、首先采用 DP 构造 S 的切割子串的图结构；

　　　　②、采用 DFS 根据图结构生成所需的 List；

public List<String> wordBreak(String s, List<String> wordDict) {
        List<String> list = new ArrayList<>();
        
        int len = s.length();
        boolean dp[] = new boolean[len + 1];
        Set<String> dict = new HashSet<>(wordDict);
        HashMap<Integer, List<Integer>> prev = new HashMap<>();
        
         //init
        dp[0] = true;
        for (int i = 1; i <= len; i++) 
            prev.put(i, new ArrayList<Integer>());
        
        //step1:construct graph
        for (int i = 1; i <= len; i++) {
            for (int j = 0; j < i; j++) {
                if(dp[j] && dict.contains(s.substring(j, i))) {
                    dp[i] = true;
                    prev.get(i).add(j);
                }
            }
        }
        
        if(!dp[len])
            return list;
        
        //step2: generate the list
        StringBuilder sb = new StringBuilder();
        dfsHelper(len, sb, prev, s, list);
        
        return list;
    }
    
    private void dfsHelper(int len, StringBuilder sb, HashMap<Integer, List<Integer>> prev, String s, List<String> list) {
        
        //base
        if(len == 0) {
            StringBuilder res = new StringBuilder(sb);
            res.deleteCharAt(0);
            list.add(String.valueOf(res));
            return;
        }
        
        List<Integer> prevIndex = prev.get(len);
        for(int i : prevIndex) {
            sb.insert(0, s.substring(i, len)).insert(0, " ");
            dfsHelper(i, sb, prev, s, list);
            sb.delete(0, (len - i) + 1);
        }
    }