113. Path Sum II

一、题目

　　1、审题

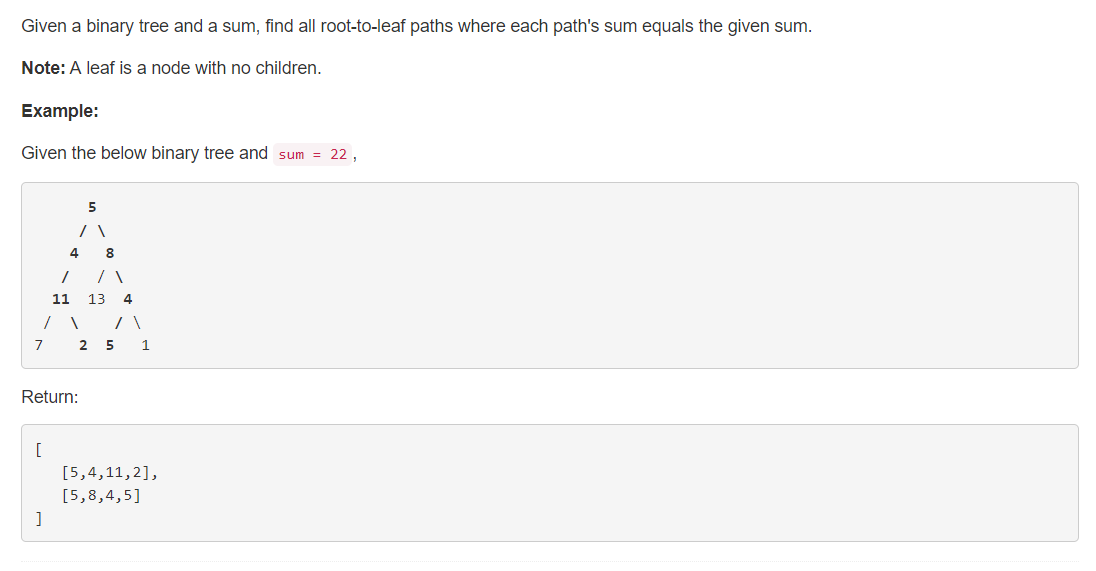
　　2、分析

　　　　给出一棵二叉树，求从根到叶节点的所有节点值和为 sum 的路径的所有节点集合。

 

二、解答

　　1、思路：

　　　　方法一、　　

　　　　　　采用递归。

　　　　　　深度优先遍历求出所有从根到叶节点的路径，将和为 sum 的进行记录。

    public List<List<Integer>> pathSum(TreeNode root, int sum) {
        List<List<Integer>> resultList = new ArrayList<List<Integer>>();
        List<Integer> targetList = new ArrayList<Integer>();
        pathSum(root, sum, resultList, targetList);
        return resultList;
    }
    
    private void pathSum(TreeNode root, int sum,
            List<List<Integer>> resultList, List<Integer> targetList) {

        if(root == null)    // 跳出条件
            return;
        targetList.add(root.val);
        if(root.left == null && root.right == null && sum == root.val) {
            resultList.add(new ArrayList<Integer>(targetList));
            targetList.remove(targetList.size()-1);
            return;
        }
        else {
            pathSum(root.left, sum - root.val, resultList, targetList);
            pathSum(root.right, sum - root.val, resultList, targetList);
            
        }
        targetList.remove(targetList.size()-1);
    }

 

　　方法二、

　　　采用后续遍历的迭代方法，进行记录和为 sum 的所有路径。

　　　注意： pre 用于记录此右节点是否访问过，否则将陷入死循环。

public List<List<Integer>> pathSum3(TreeNode root, int sum) {
        
        List<List<Integer>> resultList = new ArrayList<List<Integer>>();
        if(root == null)
            return resultList;
        
        List<Integer> targetList = new ArrayList<>();
        // postOrder
        Stack<TreeNode> stack = new Stack<>();

        int target = 0;
        TreeNode cur = root;
        TreeNode pre = null;
        
        while(cur != null || !stack.isEmpty()) {
            
            while(cur != null) {
                target += cur.val;
                targetList.add(cur.val);
                stack.push(cur);
                cur = cur.left;
            }
            
            cur = stack.peek();
            
            if(cur.right != null && cur.right != pre) {
                cur = cur.right;
                continue;
            }
            
            if(cur.left == null && cur.right == null && target == sum) 
                resultList.add(new ArrayList<Integer>(targetList));
            
            targetList.remove(targetList.size()-1);
            target -= cur.val;
            stack.pop();
            pre = cur;
            cur = null;
        }
        
        return resultList;
    }