63. Unique Paths II

一、题目

　　1、审题

　　

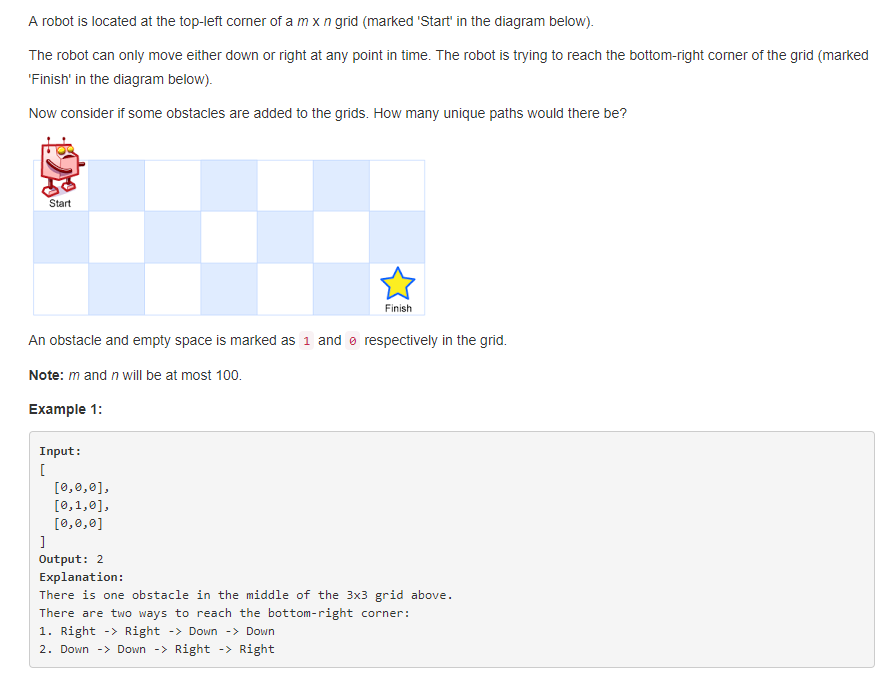
　　2、分析

　　　　只能向下、向右移动的机器人，移动过程中数值为 1 代表有障碍，不能走这一格，求到达右下角共有几种走法。

 

二、解答

　　1、思路：

　　　方法一、

　　　　新建一个数组 dp[]，从第一行开始遍历二维数组的每一行，dp[i] 用于记录这一行的第 i 个空格共有几种走法。

　　　　遍历时，若二维数组元素数值为 1， 则 dp[i] = 0 代表不可达；

　　　　若数值为 0 时，则 dp[i] += dp[i-1]； 其中 dp[i - 1] 相当于从左边一个空格走来， dp[i] 相当于从上面一个空格走来。

public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        
        int width = obstacleGrid[0].length;
        int[] dp = new int[width];
        dp[0] = 1;
        
        for(int[] row: obstacleGrid) {
            // 每一行都重填一次 dp[j]，dp[j] 代表到达这个位置能有几种走法.
            for(int j = 0; j < width; j++) {    
                if(row[j] == 1)        
                    dp[j] = 0;
                else if(j > 0)    // 跳过 j = 0
                    dp[j] += dp[j-1]; 
            }
        }
        return dp[width-1];
    }

 

　　方法二、

　　　　使用一个二维数组记录到达该格子的方法数。

　　　　当 obstacleGrid[i][j] = 1 时， dp[i][j] = 0；当  obstacleGrid[i][j] = 1 时， dp[i][j] = dp[i-1][j] + dp[i][j-1];

　　　　其中采用 dp[0][1] = 1， 使得 dp[1][1] 等于 1，用于过滤特殊情况， obstacleGrid = {{0}} 的情况。

class Solution {
    public int uniquePathsWithObstacles(int[][] obstacleGrid) {
       
        int m = obstacleGrid.length;
        int n = obstacleGrid[0].length;
        
        int[][] dp = new int[m+1][n+1];    // 考虑特殊情况， obstacleGrid = {{0}};
                
        dp[0][1] = 1;    // 使得 dp[1][1] = 1; 相当于 从 [1][1] 开始.
        
        for(int i = 1; i <= m; i++)
            for(int j = 1; j <= n; ++j)
                if(0 == obstacleGrid[i-1][j-1])
                    dp[i][j] = dp[i-1][j]+ dp[i][j-1];  
        
        return dp[m][n];
    }
}