51. N-Queens

一、题目

　　1、审题

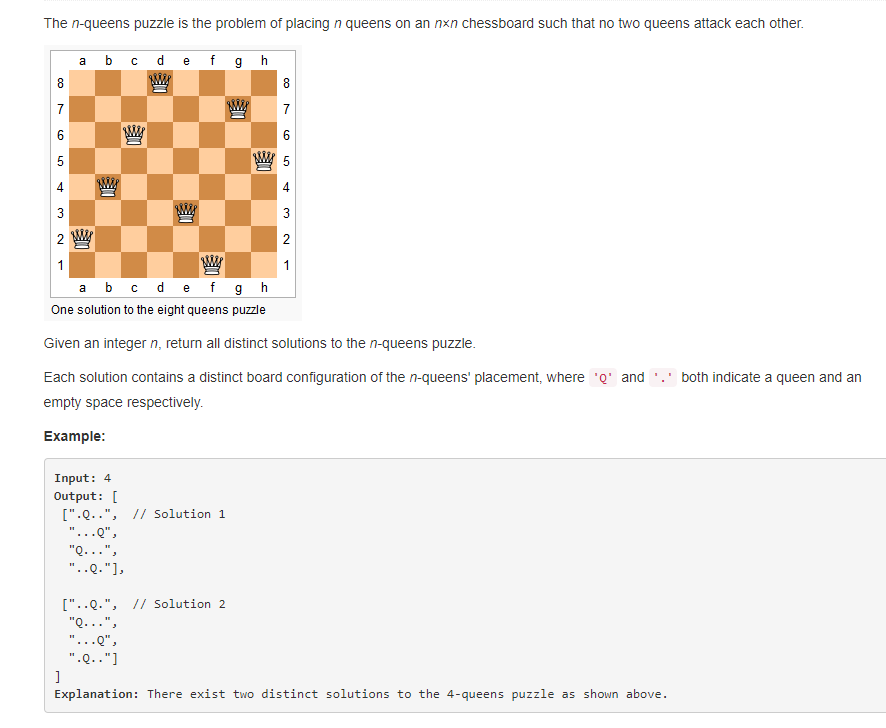
　　2、分析：

　　　　n-皇后问题： 一个 n X n的棋盘，其中，每一行、每一列、每一斜行、每一反斜行都不能有重复的皇后，输出所有的可能。

 

二、解答

　　1、思路：

　　　　典型的回溯思想，运用 DFS 方法进行求解。其中：

　　　　①、斜行： [i-1][j-1]

　　　　②、 反斜行： [i-1][j+1]

class Solution {
    public List<List<String>> solveNQueens(int n) {
        List<List<String>> resultList = new ArrayList<List<String>>();
        
        char[][] arr = new char[n][n];
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                arr[i][j] = '.'; 
            }
        }
        helper(resultList, arr, 0, n);
        return resultList;
    }
    
    private void helper(List<List<String>> resultList, char[][] arr, int row, int n) {
        // 典型的回溯格式(DFS)
        if(row == n) {
            List<String> list = new ArrayList<>();
            for(int i = 0; i < n; i++) {
                list.add(String.valueOf(arr[i]));
            }
            resultList.add(list);
            return;
        }
        else {
            for(int col = 0; col != n; ++col) {
                if(isValid(arr, row, col, n)) {
                    arr[row][col] = 'Q';
                    helper(resultList, arr, row+1, n);
                    arr[row][col] = '.'; 
                }
            }
        }
        
    }

    public boolean isValid(char[][] arr, int row, int column, int n) {
        
        // check the column
        for (int i = 0; i != row; i++) {
            if(arr[i][column] == 'Q')
                return false;
        }
        
        // check the 45 o
        for(int i = row - 1, j = column - 1; i >= 0 && j >= 0; --i, --j) {
            if(arr[i][j] == 'Q')
                return false;
        }
        
        // check the 135 o
        for(int i = row -1, j = column + 1; i >= 0 && j < n; --i, ++j)
            if(arr[i][j]== 'Q' )
                return false;
        
        return true;
    }
}