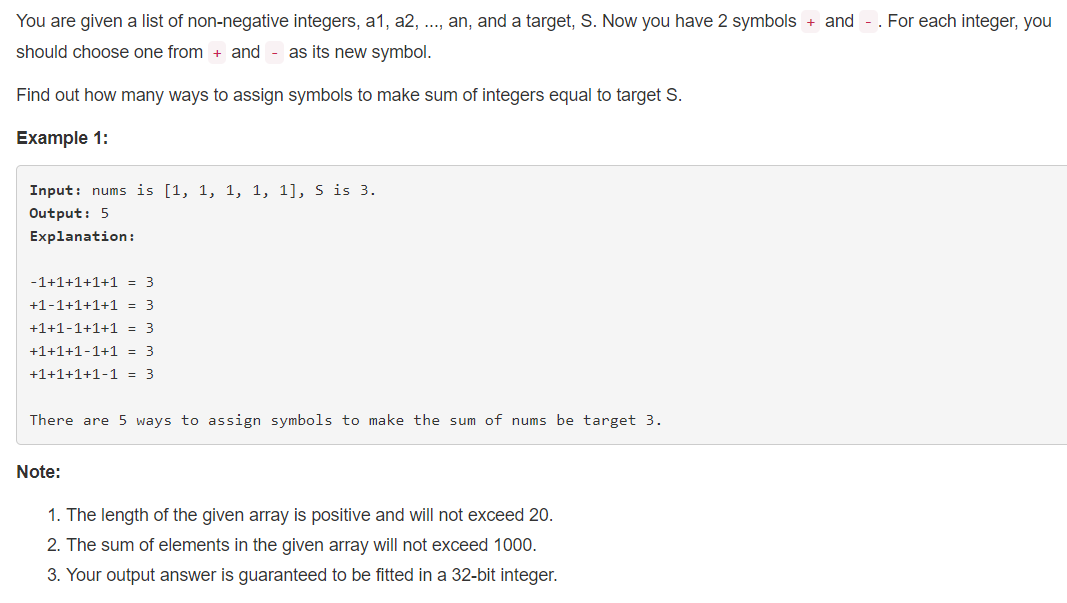
494. Target Sum

一、题目

　　1、审题　

　　

　　

　　2、分析

　　　　给出一个正整数数组。为每个元素添加 + 、- 符号，然后将元素相加，求共有多少种组合使得和为  S；

 

二、解答

　　方法一、

　　　　① 将此问题转化为取数组中若干元素，使得元素和为某一定值的问题：

　　　　假设正数集合为 P， 负数集合为 N；则有：

　　　　　　sum[P] - sum[N] = S

　　　　　　sum[P] + sum[N] + sum[P] - sum[N] = S + sum[nums]

　　　　即：

　　　　　　sum[P] = (S + sum[nums]) / 2

 

　　　　② 求若干元素和为特定值解法为：  https://www.cnblogs.com/skillking/p/10948836.html

　　　　③ 采用一维整形动态数组： dp[s + 1]。 其中 dp[i]: 表示数组 nums 中元素随意组合和 为 i 的组合个数。

　　　　④ 最终返回 dp[s]

   public int findTargetSumWays(int[] nums, int s) {
        int sum = 0;
        for(int n : nums) 
            sum += n;
        
        if(sum < s || (s + sum) % 2 == 1)
            return 0;

        return subsetSum(nums, (s + sum) >>> 1);
    }
    
    private int subsetSum(int[] nums, int s) {
        int[] dp = new int[s + 1];
        dp[0] = 1;    // 在 nums 中取若干个元素求和，和为 0 的组合共 1 个
        for(int n: nums) {
            for (int i = s; i >= n; i--) {
                dp[i] += dp[i - n];
            }
        }
        return dp[s];
    }