416. Partition Equal Subset Sum

一、题目

　　1、审题　

　　

　

　　2、分析

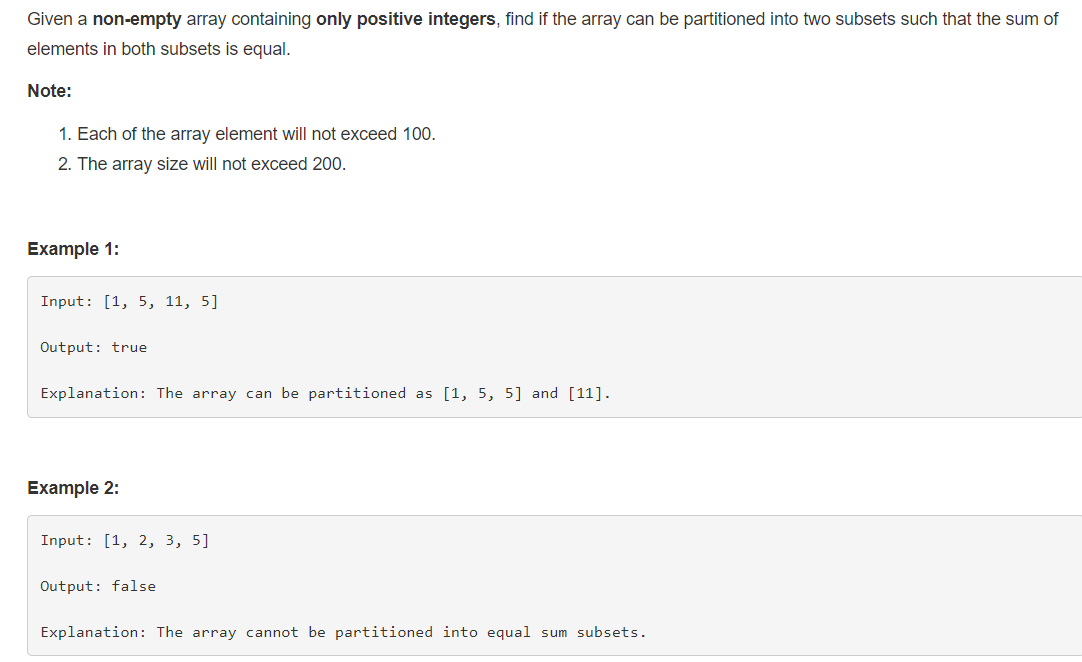
　　　　给出一个整形数组，判断是否能将其拆分成两个元素和相等的子数组。

 

二、解答

　　1、思路

　　　　① 将数组所有元素求和得到 sum， 若 sum %2 == 1 ，则不可切分。

　　　　② 将 sum 除以 2，即 sum /= 2； 则 问题变为：从 数组中取出若干个元素，使得其和为 sum。即 0/1 背包问题。

　　　　③ 采用布尔型二维动态数组 dp[][];  dp[i][j]: 表示数组中前 i 个元素中是否能存在某个组合使得元素和为 j 。

　　　　  　　若 dp[i][j]，取出的组合中不包含数组第 i 个元素，即 nums[i - 1]。则 dp[i][j] = dp[i - 1][j]

　　　　　　  若 dp[i][j] 取出的组合中包含数组第 i 个元素， 即 nums[i - 1]。则 dp[i][j] = dp[i - 1][ j - nums[i - 1]]；

　　　　　　所以 dp[i][j] = dp[i-1][j]  ||  dp[i-1][j - nums[i - 1]]

　　　　最终返回结果为 nums[n][sum] ； 其中 n 为数组长度。

    public boolean canPartition(int[] nums) {
        int sum = 0;
        for(int n : nums) 
            sum += n;
        if((sum & 1) == 1)
            return false;
        
        sum /= 2;
        int n = nums.length;
        boolean[][] dp = new boolean[n + 1][sum + 1];　　// dp[i][j]: 前 i 个数能否有组合可以组成 和为 j 。
        for (int i = 0; i < dp.length; i++) {
            Arrays.fill(dp[i], false);
        }
        // 0 个数构成的和为 0
        dp[0][0] = true;
        // i 个数中选取出 x 个，构成的和为 0
        for (int i = 1; i < n + 1; i++) {
            dp[i][0] = true;
        }
        // 0 个数中选取出 x 个，构成的和为 i (i > 0)
        for (int i = 1; i < sum + 1; i++) {
            dp[0][i] = false;
        }
        
        for (int i = 1; i < n + 1; i++) {
            for (int j = 1; j < sum + 1; j++) {
                // 1、不使用 nums[i - 1], 即第 i 个数
                dp[i][j] = dp[i - 1][j];
　　　　　　　　　　// 2、 如果使用 nums[i - 1]， 即第 i 个数。 看是否能组成和为 j 
                if(j >= nums[i - 1]) 
                    dp[i][j] = (dp[i][j] || dp[i - 1][j - nums[i - 1]]);
            }
        }
        return dp[n][sum];
    }

 

　　优化：

　　　　使用一维数组 boolean 型！ 其中 dp[sum] 表示 能否组成和为 sum 的组合。

    public boolean canPartition2(int[] nums) {
        int sum = 0;
        
        for (int num : nums) {
            sum += num;
        }
        
        if ((sum & 1) == 1) {
            return false;
        }
        sum /= 2;
        
        boolean[] dp = new boolean[sum+1];
        
        Arrays.fill(dp, false);
        dp[0] = true;
        for(int num: nums) {
            for(int i = sum; i > 0; i--) {
                if(i >= num)
                    dp[i] = dp[i] || dp[i - sum];
                else 
                    break;
            }
        }
        return dp[sum];
    }