300. Longest Increasing Subsequence

一、题目

　　1、审题

　　

　　2、分析

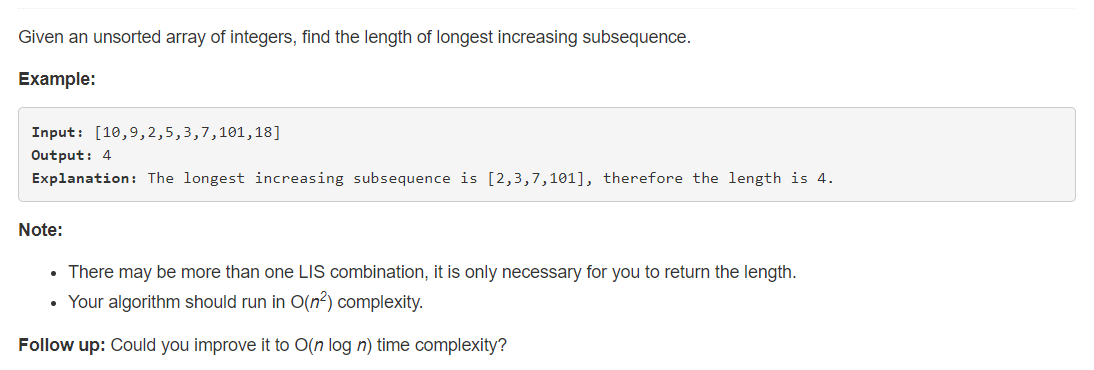
　　　　给出一个无序的整形数组，求其中递增的最大序列的元素个数。

 

二、解答

　　1、思路

　　　　方法一、

　　　　　　采用 dp 数组，长度为 nums 的元素个数。

　　　　　　①、dp[index] 记录当前下标 index 对应元素与前边的数组元素组成的最大递增序列的个数。

　　　　　　②、dp 所有元素初始化为 1。 当此元素值比前头 下标 i 的元素大时，dp[index] = MAX[dp[index], dp[i] + 1]。

　　　　　　③、返回 dp 中的最大值。

   public int lengthOfLIS(int[] nums) {
        int len = nums.length;
        int[] dp = new int[len];
        Arrays.fill(dp, 1);;
        for (int i = 1; i < len; i++) {
            for (int j = i - 1; j >= 0; j--) {
                if(nums[i] > nums[j])
                    dp[i] = Math.max(dp[i], dp[j] + 1);
            }
        }
        int res = 0;
        for (int i = 0; i < len; i++) {
            res = Math.max(res, dp[i]);
        }
        return res;
    }

 

　　方法二、

　　　　维护一个新数组  tails。

　　　　①、tails 存放最优状态的递增序列。后边出现的元素 x 有两种状况：

　　　　　　a、 x比 tails 中所有元素都大，则 tails 放在尾部。

　　　　　　b、tails[i - 1] < x < tails[x]， 则 tails[i]  = x;

　　　　②、故 更新 tails 数组可以采用 二分查找。最终返回的是 tails 数组中的元素的个数。

    public int lengthOfLIS2(int[] nums) {
        int[] tails = new int[nums.length];
        int size = 0;
        for(int x: nums) {
            int i = 0, j = size;
            while(i != j) {
                int m = (i + j) / 2;
                if(tails[m] < x)
                    i = m + 1;
                else 
                    j = m;
            }
            tails[i] = x;
            if(i == size)
                size++;
        }
        return size;
    }