机器模型简介（二）：广义线性模型

       广义线性模型（GLMs）扩展了普通线性回归模型，可以分析非正态分布的结果变量以及相应均值的函数。假设第i个观察是一个期望值为的随机变量的实现。当用线性模型来学习随机变量Y的时候，我们指明它的期望是K个未知参数以及自变量的线性组合：

                                                       

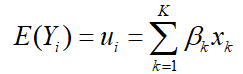
      这是一个线性回归模型，为了创建一个更加通用的模型，我们引入变量，与的关系为：

                                                       

       这是一个广义线性模型，与有许多可能的关系函数，Logit模型是分类模型中常用的广义线性模型。它归纳或描述一个分类变元和一组预测变元的关系，分类变元可以取二值，也可以取多值，其取值可以是无序的，也可以是有序的。下面我们将分别对这几种情况展开讨论。

       假设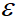服从logistic分布，将关系函数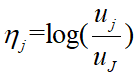带入上式，我们指定了一个结果是多类别Logit模型。用logit形式表达时，模型指定为：

                                                  

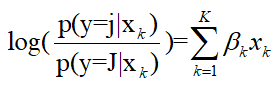
      当总类别数J=2时，等式可以简化为二分模型，Logit模型的累计概率可以写为：

                       

       作为广义线性模型的―种，经典线性模型的基本原则都可以应用。与线性回归一样，我们要选择一个拟合得好的模型去描述因变元与预测变元之间的关系。经典线性模型通常利用最小二乘法来估计回归系数，当因变元服从正态分布时，回归系数的估计量具有很多良好的统计特性。不幸的是，对于服从伯努利分布或多项分布的因变元，这些特性不再成立。对于Logit线性模型，通常使用极大似然法来估计回归系数。

       Logit模型即逻辑回归，是一个线性分类模型而不是回归模型。逻辑回归在文献中也称为最大熵分类(MaxEnt) 或者 log-linear classifier。scikit-learn中逻辑回归的实现为 LogisticRegression 类。它可以拟合含L2或者L1正则化项的多类逻辑回归问题。

       以下是用python3实现逻辑回归的小例子。求解可得w00 = -0.16，w01 = -0.35，w02 = 0.4。

from sklearn import linear_model
clf = linear_model.LogisticRegression()
clf.fit([[1.2, 1.3], [1.1, 1.4], [1.1, 2.3], [0.8, 1.9]], [0, 0, 1, 1])
print('w0:', clf.intercept_) 
print('wi:', clf.coef_)
print(clf.predict([[0.9, 0.98]]))

       如果已经建立了logistic回归模型，则可以根据模型，预测在不同的自变量情况下，发生某种情况的概率有多大。logistic回归几乎已经成了流行病学和医学中最常用的分析方法，因为它与多重线性回归相比有很多的优势。实际上有很多其他分类方法，只不过Logistic回归是最成功也是应用最广的。