清北
笔记
【问题描述】
给定一个长度为m的序列a,下标编号为1~m。序列的每个元素都是1~n的
整数。定义序列的代价为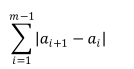
你现在可以选择两个数x和y,并将序列a中所有的x改成y。x可以与y相等。
请求出序列最小可能的代价。
【输入格式】
输入第一行包含两个整数n和m。第二行包含m个空格分隔的整数,代表序
列a。
【输出格式】
输出一行,包含一个整数,代表序列最小的代价。
【样例输入 1】
4 6
1 2 3 4 3 2
【样例输出 1】
3
【样例输入 2】
10 5
9 4 3 8 8
【样例输出 1】
6
【样例解释】
样例 1 中,最优策略为将 4 改成 3。样例 2 中,最优策略为将 9 改成 4。
【数据规模和约定】
对于30%的数据,n,m<=100.
对于60%的数据,n,m ≤ 2000。
对于100%的数据,1 ≤ n,m≤ 100,000。
题解:由于题目要求序列的最小代价,因此原代价-max(x与它在序列中左右两边数的差值-替换他的y在序列中左右两边数的差值)即为答案。
考虑用哪个数替换x:
当与x相邻的数有奇数个时,取中间的数为y。因为改变中间的数对两边的贡献一样。比如样例1:与2相邻的为1,3,3,原本与2相邻的代价为1,1,1。将2替换为3时,代价为2,0,0.左边的代价加1,右边的代价-1.相当于改变中间的数对其两边代价无影响,影响的只是中间数的代价,因此取中间数为y,此时中间数代价为0。而若是取其他的数,对其左边或右边代价产生影响。
当与y相邻的数有偶数个时,取中间两个数之间的任意数为y均可。比如样例1:与3相邻的为2,2,4,4。取2<=y<=4均可。原本与3相邻的代价为1,1,1,1。总代价为4.将3替换为2时,代价为0,0,2,2.总代价为4.将3替换为4时,代价为2,2,0,0,总代价也为4.

#include<cstdio> #include<iostream> #include<cstring> #include<algorithm> #include<cstdlib> #define ll long long #define N 100010 using namespace std; ll n,m,ans=0x7fffffff/3,sum(0); ll a[N],b[N],c[N]; ll f[N][3],ff[N]; bool fi[N]={0}; void erfen(int k,int l,int r) { if (l>r) return ; int mid=(l+r)>>1; a[0]=mid; int ki=b[k],sum1(0),sum2(0); if (mid-a[b[k]-1]>0) sum1+=mid-a[b[k]-1]; else sum2+=mid-a[b[k]-1]; if (a[b[k]+1]-mid>0) sum2+=mid-a[b[k]+1]; else sum1+=mid-a[b[k]+1]; while (ff[ki]) { if (mid-a[ff[ki]-1]>0) sum1+=mid-a[ff[ki]-1]; else sum2+=mid-a[ff[ki]-1]; if (a[ff[ki]+1]-mid>0) sum2+=mid-a[ff[ki]+1]; else sum1+=mid-a[ff[ki]+1]; ki=ff[ki]; } ans=min(ans,sum-f[k][0]+f[k][1]-f[k][2]+sum1-sum2); if (-sum2>sum1) erfen(k,mid+1,r); else erfen(k,l,mid-1); } int main() { freopen("note.in","r",stdin); freopen("note.out","w",stdout); scanf("%I64d%I64d",&n,&m); for (int i=1;i<=m;i++) { scanf("%I64d",&a[i]); fi[a[i]]=1; a[0]=a[1]; if (a[i]-a[i-1]>0) { f[a[i]][0]=a[i]-a[i-1],sum=sum+a[i]-a[i-1]; f[a[i-1]][2]=a[i]-a[i-1]; } else { f[a[i]][1]=a[i]-a[i-1],sum=sum+a[i-1]-a[i]; f[a[i-1]][2]=a[i-1]-a[i]; } } for (int i=m;i>=1;i--) { if (!b[a[i]]) b[a[i]]=i; else ff[i]=b[a[i]],b[a[i]]=i; } for (int i=1;i<=n;i++) if (fi[i]) erfen(i,0,n); printf("%I64d\n",ans); fclose(stdin); fclose(stdout); return 0; }
考试的时候从0~n枚举将x变为几。

#include<cstdio> #include<iostream> #include<cstring> #include<algorithm> #include<ios> #include<vector> #define ll long long using namespace std; const int N = (int) 1e5; vector<int> v[N+10]; int a[N+10]; int n,m; ll ans(0),sum(0); int main() { freopen("note.in","r",stdin); freopen("note.out","w",stdout); scanf("%d%d",&n,&m); for (int i=1;i<=m;i++) scanf("%d",&a[i]); for (int i=1;i<=m;i++) { if (i!=1&&a[i]!=a[i-1]) v[a[i]].push_back(a[i-1]);//将与a[i]相邻的不同的数储存进数组 if (i!=m&&a[i]!=a[i+1]) v[a[i]].push_back(a[i+1]); } for (int i=1;i<=n;i++) { int k=v[i].size(); if (k) { sort(v[i].begin(),v[i].end()); ll ki=v[i][k>>1]; //当k为奇数时,取中间的数,其对两边数的贡献是一样的。 //当k为偶数时,取中间两个数之间的任意数都可,对其两边数的贡献一样。 ll sum1(0),sum2(0); for (int j=0;j<k;j++) { sum1+=(ll)abs(i-v[i][j]); sum2+=(ll)abs(ki-v[i][j]); } ans=max(ans,sum1-sum2); sum+=sum1; } } cout<<sum/2-ans<<endl;//由于a[i+1]-a[i]在计算a[i]时计算了一次。 //在a[i+1]时又计算了一次,因此除以2 fclose(stdin); fclose(stdout); return 0; }
括号
【问题描述】
有一个长度为n的括号序列,以及k种不同的括号。序列的每个位置上是哪
种括号是随机的,并且已知每个位置上出现每种左右括号的概率。求整个序列是
一个合法的括号序列的概率。
我们如下定义合法括号序列:
空序列是合法括号序列;
如果A是合法括号序列,那么lAr是合法括号序列,当且仅当l和r是同种
的左右括号;
如果A和B是合法括号序列,那么AB是合法括号序列。
【输入格式】
输入第一行包含两个整数n和k。接下来的输入分为n组,每组k行。第i组第
j行包含两个实数l[i,j]和r[i,j],分别代表第i个位置上是第j类的左括号和右括号
的概率。
【输出格式】
输出一行,包含一个实数,代表序列是合法括号序列的概率。建议保留至少
5 位小数输出。只有当你的输出与标准答案之间的绝对误差不超过10 −5 时,才会
被判为正确。
【样例输入 1】
2 1
1.00000 0.00000
0.00000 1.00000
【样例输出 1】
1.00000
【样例输入 2】
4 1
0.50000 0.50000
1.00000 0.00000
0.00000 1.00000
0.50000 0.50000
【样例输出 2】
0.25000
【数据规模和约定】
对于20%的数据,n ≤ 50,k = 1,所有位置的概率非 0 即 1。
另外有 30%的数据,n ≤ 34,k = 1,前 10 个和后 10 个位置的所有概率都
是 0.5,中间剩余位置的概率非 0 即 1。
80%的数据,n,k ≤ 50。
对于100%的数据,1 ≤ n ≤ 200,1 ≤ k ≤ 50。
考场:考试的时候只想到了50%的数据怎么做,画蛇添足加上了关于输出结果是0的判断,只得了30分,然而删掉后,可以得50分。好伤心。
题解:空序列直接判断n是否等于0.用f数组储存第二种括号序列概率,用g数组储存第三种括号序列概率。
枚举序列的长度l,f[i][i+l-1]+=(f[i+1][i+l-2]+g[i+1][i+l-2])*L[i][j]*R[i+l-1][j];//在合法序列两边加上一对括号,概率就是中间是合法括号序列的概率*序列开头是左括号的概率*序列结尾是右括号的概率。
g[i][i+l-1]+=f[i][j]*(f[j+1][i+l-1]+g[j+1][i+l-1]);//前一部分括号序列为f的概率和后一部分是合法括号序列的概率。//为什么前一部分只有f的概率?例如:()()()这个好像可以从位置5Chu前一部分分成g序列,后一部分f序列,但实际当你在求位置2的时候,这种情况已经计算了。

#include<cstdio> #include<iostream> #include<cstring> #include<algorithm> #include<cstdlib> #define ll long long #define N 210 using namespace std; int n,k; double a[N][N][3],f[N][N][N]={0},ans(0); int num[N][2]={0}; int main() { freopen("brackets.in","r",stdin); freopen("brackets.out","w",stdout); scanf("%d%d",&n,&k); for (int i=1;i<=n;i++) for (int j=1;j<=k;j++) { double x,y; scanf("%lf%lf",&x,&y); a[i][j][1]=x; a[i][j][2]=y; } for (int i=1;i<=k;i++) f[1][i][1]=a[1][i][1]; for (int i=2;i<=n;i++) { for (int ki=1;ki<=k;ki++) for (int j=0;j<i;j++) { f[i][ki][j+1]+=f[i-1][ki][j]*a[i][ki][1]; if (j-1>=0) f[i][ki][j-1]+=f[i-1][ki][j]*a[i][ki][2]; } } for (int i=1;i<=k;i++) ans+=f[n][i][0]; printf("%.5lf\n",ans); fclose(stdin); fclose(stdout); return 0; }

#include<cstdio> #include<iostream> #include<cstring> #include<algorithm> #define N 210 #define M 60 using namespace std; int n,k; double L[N][M],R[N][M],f[N][N]={0},g[N][N]={0}; int main() { freopen("brackets.in","r",stdin); freopen("brackets.out","w",stdout); scanf("%d%d",&n,&k); if (n==0) printf("%0.5lf\n",1);//空序列 else { for (int i=1;i<=n;i++) for (int j=1;j<=k;j++) scanf("%lf%lf",&L[i][j],&R[i][j]); for (int i=1;i<=n;i++) f[i+1][i]=1; for (int l=2;l<=n;l+=2) for (int i=1;i<=n-l+1;i++) { for (int j=1;j<=k;j++) f[i][i+l-1]+=(f[i+1][i+l-2]+g[i+1][i+l-2])*L[i][j]*R[i+l-1][j]; for (int j=i+1;j<i+l-1;j+=2) g[i][i+l-1]+=f[i][j]*(f[j+1][i+l-1]+g[j+1][i+l-1]); } double ans=f[1][n]+g[1][n]; printf("%.5lf\n",ans); } fclose(stdin); fclose(stdout); return 0; }
城堡
【问题描述】
给定一张N个点M条边的无向连通图,每条边有边权。我们需要从M条边中
选出N − 1条, 构成一棵树。 记原图中从 1 号点到每个节点的最短路径长度为Di ,
树中从 1 号点到每个节点的最短路径长度为? ? ,构出的树应当满足对于任意节点
i,都有Di = Si 。
请你求出选出N − 1条边的方案数。
【输入格式】
输入的第一行包含两个整数N和M。
接下来M行,每行包含三个整数u、v和w,描述一条连接节点u和v且边权为
w的边。
【输出格式】
输出一行,包含一个整数,代表方案数对2^31 − 1取模得到的结果。
【样例输入】
3 3
1 2 2
1 3 1
2 3 1
【样例输出】
2
【数据规模和约定】
对于20%的数据,2<=N<=5,M<=10.
对于50%的数据,满足条件的方案数不超过 10000。
对于100%的数据,2≤ N ≤ 1000,N-1 ≤ M ≤ N(N-1)/2,1<=w<=100.

#include<cstdio> #include<iostream> #include<cstring> #include<algorithm> #define N 1100 #define NN 1000010 #define ll long long using namespace std; int n,m,num(0),Head,Tail; int head[N],team[NN]; ll sum[N]={0},ans(1); ll dis[N]; bool f[N]; const ll M=1<<31-1; struct node { int v,t,pre; }e[NN]; void xx() { Head=0;Tail=1; memset(f,0,sizeof(f)); memset(team,0,sizeof(team)); team[1]=1;f[1]=1;sum[1]=1; } void add(int from,int to,int w) { e[++num].v=to; e[num].t=w; e[num].pre=head[from]; head[from]=num; } void spfa() { for (int i=1;i<=n;i++) dis[i]=0x7fffffff; dis[1]=0;f[1]=1;team[1]=1;Head=0;Tail=1; while (Head<=Tail) { int ki=team[++Head]; f[ki]=0; for (int i=head[ki];i;i=e[i].pre) { int u=e[i].v; if (dis[u]>dis[ki]+e[i].t) { dis[u]=dis[ki]+e[i].t; if (!f[u]) { f[u]=1; team[++Tail]=u; } } } } } int main() { freopen("castle.in","r",stdin); freopen("castle.out","w",stdout); scanf("%d%d",&n,&m); for (int i=1,x,y,z;i<=m;i++) { scanf("%d%d%d",&x,&y,&z); add(x,y,z); add(y,x,z); } spfa(); xx(); while (Head<=Tail) { int ki=team[++Head]; f[ki]=0; for (int i=head[ki];i;i=e[i].pre) { int u=e[i].v; if (dis[u]==dis[ki]+e[i].t) { sum[u]++; if (sum[u]>=M) sum[u]-=M; if (!f[u]) team[++Tail]=u,f[u]=1; } } } for (int i=1;i<=n;i++) ans=(ans*sum[i])%M; cout<<ans<<endl; fclose(stdin); fclose(stdout); return 0; }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号