HeteSpaceyWalk: A Heterogeneous Spacey Random Walk for Heterogeneous Information Network Embedding论文阅读笔记
写博以供备份。
HeteSpaceyWalk: A Heterogeneous Spacey Random Walk for Heterogeneous Information Network Embedding (用于异构信息网络嵌入的异构空间随机游走)
现有框架及问题:
分为两步,1 基于一条或多条元路径的随机游走 2 使用 skip gram 生成节点表示 (skip gram 使用中心节点去预测随机游走路径的上下文节点)
问题:
很少注意到基于元路径随机游走的高阶马尔可夫性质,尤其是平稳性问题
元路径需要很强的领域知识,给不同元路径赋合适的权重也是问题 (在本文中主要解决的是给不同元路径赋权重的问题,即通过一定算法来选取下一个节点的类型和具体节点)
本文:
-
将元路径引导的随机游走系统化为高阶马尔可夫链过程
-
提出一种异构个性化空间随机游走用来生成异构邻域,以有效实现节点之间预期平稳分布
实际上执行的为基于特殊元图的随机游走 (不会严格的限制元路径上的走动,允许间距和跳过中间的琐碎步骤),元路径和元模式都是元图的特殊形式,特殊元图的不同:
- 集成了多个元路径,这些元路径是通过折叠用户提供的原始元路径自动生成的
- 在元图中选择哪条元路径是的概率是动态自适应的
- 数学上保证与原始的元路径引导的高阶马尔可夫随机游走有相同的 unique limiting stationary distribution
- 允许间距和跳过中间琐碎步骤,更高效
-
提出了一个通用的可扩展框架,以利用异构个性化空间随机游动来学习由元路径,元图和元模式分别指导的HIN中多种类型节点的嵌入,即
- 提出 spaceymetapath (hetespaceywalk + skip gram),对任意用户给出的元路径,都能对不同类型节点生产有语义的 embeddings
- 提出 spaceymetagraph 和 spaceymetaschema,即 metagraph based 和 metascheme based heterogeneous spacey random walk based embeddings
1.meta-path based HIN embeddings
通过扩展传统的基于元路径的随机游走 (给定一条任意元路径,学习其中所有节点的有语义的表示) 来完成
-
HIN 上的随机游走
即在 path ranking algorithm (PRA) 中计算相似性

PAl,Al+1 (vi, vj) 为在类型为 Al 的节点 vi 执行随机游走时,选择类型为 Al+1 的节点 vj 的概率,WAl,Al+1 为类型 Al 和类型Al+1 的邻接矩阵,DAl,Al+1 为 degree matrix:
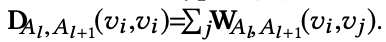
在元路径 P = (A1 → A2 → ... →AL+1) 中,用如下式子来定义在这条元路径上类型 A1 的节点和类型 AL+1 节点的相似性

这其实是一个 ad hoc 定义的 hitting/commuting probability,并且实际期望的 hitting/commuting probability 可以由遵循元路径限制的随机游走的 stationary distribution 来近似
现有的方法大都是直接使用这种随机游走采样而忽略了高阶马尔可夫链属性,特别是忽略了 limiting stationary distribution (这对描述随机游走的长期行为很重要),所以需要提出改进
-
高阶马尔可夫链
定义:对于任意元路径 P = (A1 → A2 → ... →AL+1),若 P 可以被划分为一组唯一的 k 长度的元路径 (Al → Al+1 → ... →Al+k),且满足最后一个 k 状态由 (Al → Al+1 → ... →Al+k-1) 决定且状态只能为 Al+k,则称为 k 阶马尔可夫链。
随后,可将这些长度为 k 的元路径的标准化后的通勤矩阵或邻接矩阵串联起来来获得 k 阶马尔可夫链的转移概率,这个概率用来指导基于 P 的随机游走
定义一个基于元路径的二阶马尔可夫随机游走的二阶超矩阵(三维张量)
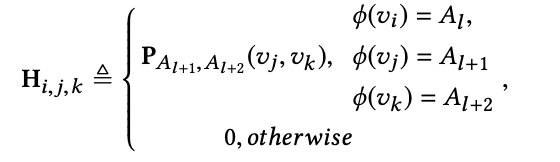
其中,Hi,j,k 为节点 vk 在 last 节点为 vj 且 second last 节点为 vi 的情况下的转移概率,AlAl+1Al+2 为一个二阶马尔可夫链 (由基础的元路径生成), φ(·) 为节点类型映射
问题是存在一些不重要的walk,由高阶马尔可夫链的性质,一个节点在元路径上的转移往往基于之前数个状态而不是之前唯一一个状态,所以一个节点在 walk 中可能是多余的
举例: 有三种节点,A 作者 P 文章 V 期刊
一个元路径 a1 → p1 → v1 → p1 → a2 (APVPA) 与 a1 → p1 → a2 (APA) 表示的相同的含义 ,所以 p1 → v1 → p1 是多余的步数从而可跳过
即可以不严格遵循元路径进行随机游走从而进行简化,有一定概率可以偶尔跳过中间的多余的步骤,即对于任意一条元路径
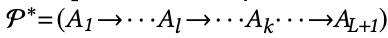
当 Al = Ak 时,都有一定概率可以进行一个更快的随机游走,即对元路径进行折叠,且折叠后的语义与原来的元路径相同
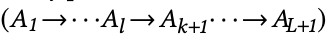
这就需要引出空间随机游走策略
-
异构个性化空间随机游走
对于给定的高阶马尔可夫链,提供了有效的替代值并保证收敛到同样的 limiting stationary distribution
基于二阶马尔可夫链的元路径上的 hetespaceywalk:一个随机过程
给定一个状态或节点序列:
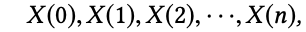
当前序列中,最后一个状态为 X (n),现用如下公式来选择 second last 状态 Y (n):
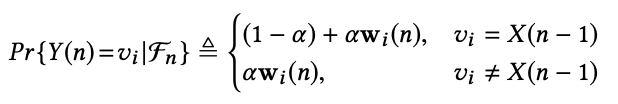
然后用如下公式,基于 X (n) 和 Y (n) 确定 X (n+1)
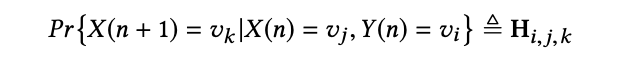
其中,Fn 为随机变量 X (i) 上的 σ-field(在数学中,某个集合 X 上的σ-代数又叫σ-域,是 X 的幂集的子集合。这个子集满足对于补集运算和可数个并集运算的封闭性)且X (0) 为初始状态,α 为控制用户个人行为的超参数,W (n) 为第 n 步的 occupation vector,定义如下
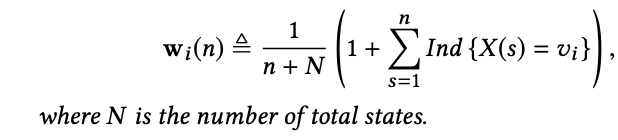
这个过程可以简单描述为,当 random walker 在第 n 步时走到 X (n) 时,有 α 的概率跳过并忘记 second last state,即 X (n-1) ,并创造一个新的历史状态 Y(n) 来替代原有的 second last state X(n),然后转移到 X (n+1) 状态上,在这个过程中,personalization 主要就体现在 α 上,当 α = 0时,就和普通的二阶马尔可夫链随机游走一样。
可以说,在原本的基于多条元路径的随机游走过程中,给每条元路径赋值合适的权重是一个很大的问题,在空间随机游走中,自适应的调整了遵循原来的元路径或折叠过的子元路径的概率,并且不会有用户关注之外的其他异构信息
-
基于空间随机游走的 embedding
将异构个性化空间随机游走生成的节点序列,使用 skip gram 来学习 node embeddings
其目标函数为:
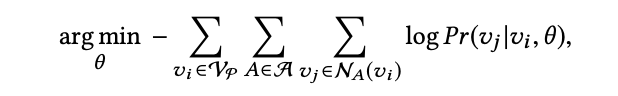
其中,Vp 为元路径 P 下的 paths corpus,NA(vi) 为节点 v 类型为 A 的邻居集合,对于每对节点 (vi, vj),联合概率遵从如下 softmax 函数:
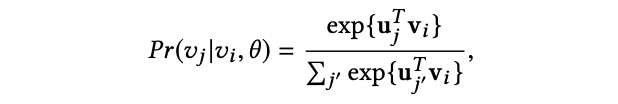
其中,uj 是 vj 的上下文向量,向量 vi 是节点 vi 的表示向量
此外,还使用了负采样方法进行优化:
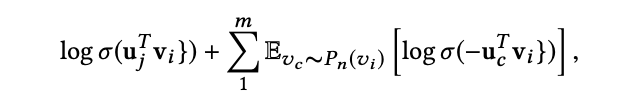
其中,
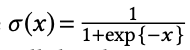
且 Pn(vi) 为采样分布
2.meta-graph based HIN embeddings
问题的难点是如何以适当的比例连接这些高阶马尔可夫链,即在元图中分配每条元路径的概率
将之前 meta-path based HIN embeddings 中的选取 Y(n) 的原理扩展到分支选择中,即元图中到达一个节点选择哪条元路径的问题
一个含有 M 个二阶马尔可夫链的元图 Ts = (As, Rs),聚合后的转移超矩阵为:
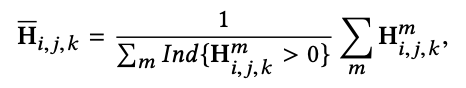
其中,Hm 是第 m 条元路径的转移概率,同时使用上文选择 Y(n) 的方法选择 Y(n) 和 X(n+1),其中使用下式选择 X(n+1) 节点的类型
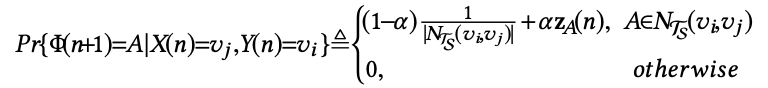
使用下式选择 X(n+1) 的节点,即在确定类型后再选择同类型中的节点:
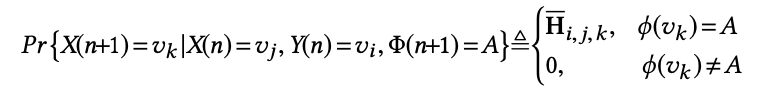
其中,NTs(vi, vj) 为边 (φ(vi), φ(vj)) 后继类型的集合,z(n) 为在第 n 步的 partial occupation vector 如下:
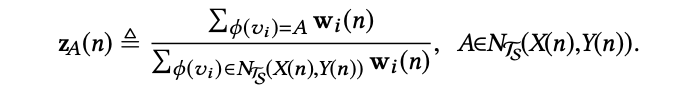
整个过程可以视作,在上文中提到的选取 Y(n) 的基础上,用同样的算法选取下一个节点即 X(n+1) 的类型和具体节点
基于上述过程,生成邻域使用 skip gram 进行 HIN embeddings
3.meta-schema based HIN embeddings
提出这个方法让使用者无须构造元路径或元图,将上述两种方法扩展为基于 meta-scheme 的 embedding,在 meta-scheme 中,没有重复类型的节点,即为一阶马尔可夫链,从而不需要选择 Y(n) 的过程,但需要选择 X(n+1) 的过程
其中,使用下式选择 X(n+1) 节点的类型

使用下式选择 X(n+1) 的节点,即在确定类型后再选择同类型中的节点:
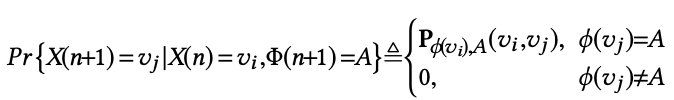
其中,NTg(vi) 为 φ(vi) 的邻接类型的集合,z(n) 为:

以上过程可以视作一阶马尔可夫链的过程,并且动态选择了下一个节点的类型以及该类型中的某一个节点

