[OI学习笔记]从蒟蒻的角度理解动态规划(DP)——从暴力搜索到动态规划

前言

　　作为一个蒟蒻，一直对动态规划（DP）一知半解。。。

    今天一定要弄懂DP！

 

斐波那契数列

    从一个问题开始：

斐波那契数列

    1,1,2,3,5,8,13,21,34,55,89......

    斐波那契数列前两项为1，对于除前两项的第i向，f[i]=f[i-1]+f[i-2]

     作为一个蒟蒻，当然是想到用爆搜。。。

 

(A)暴力搜索

    先上一个爆搜的代码：

int dfs(int n){
    if(i<3)return 0;
    return dfs(n-1)+dfs(n-2);
} 

 

    但是，这样的时间复杂度显然太高，因为在搜索的过程中重复做了很多同样的操作，如图：

    

 

  

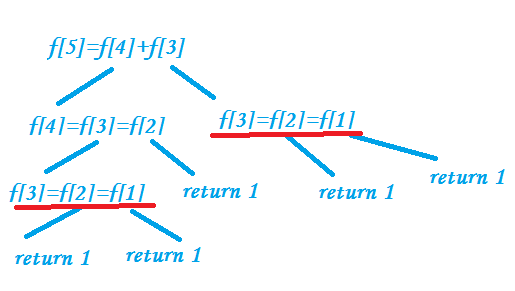
   (B)记忆化搜索

    好吧，我们再进行优化，可以用一个数组存储已经算出来的值，我们称之为记忆化搜索，这种方法的优化的确很大，基本上能做到瞬间出解。

    记忆化搜索代码：

#include<cstdio>
#define MAXN 10086
int f[MAXN]{0};
int dfs(int n){
    if(f[n]!=0)return f[n];
    if(i<3)return 0;
    return dfs(n-1)+dfs(n-2);
} 

   

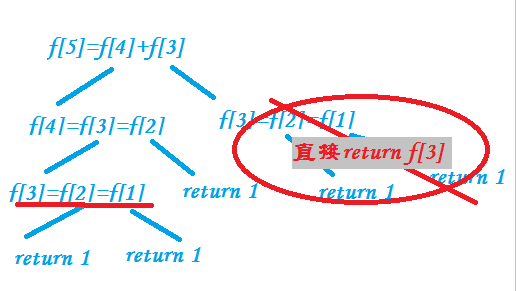
　 但是，这种做法实在是太不雅观，我要想点高级点的做法

    搜索是一个递归结构，把复杂化为简单，再有简单的问题综合成复杂问题，如果把思路反过来，用一个递推的结构，直接从简单到复杂呢？

 

(C)递推

    将一个难以解决的问题拆分成几个简单问题，从简单问题出发进一步解决大问题

    先上代码，继续解释

#include<cstdio>
#define MAXN 10086
int n,f[MAXN]{0};
int main(){
    f[1]=f[2]=1;
    scanf("%d",&n);
    for(int i=3;i<=n;i++)
        f[i]=f[i-1]+f[i-2];
    printf("%d",f[n]);
}

   

---

 

用一些简单的FAQs来理解： 

 

    一、怎么样的问题可以用DP解决？

 

        1）满足最优子结构性质：大问题的最优解由小问题的最优解组成，即每个小问题的最优解综合而成的大问题的解是最优的

        2）满足无后效性：每个状态的值求出后，这个状态的子状态不再影响今后求得的状态，即该状态在求值方面不再用得上

        3）问题有边界：大问题存在简单到足以直接出解的子问题

 

二、一个DP程序的基本构成？

 

    1）状态：像刚刚的程序，斐波那契数列的每一项就是一个状态

    2）状态转移方程：将一个状态的值用另一个(或几个)状态表示粗来，如;f[n]=f[n-1]=f[n-2]。

 

    三、最后一个问题，DP和记忆化搜索的区别？

 

    1）搜素在结构上是递归的，而DP是递推的。

    2）递推在时间复杂度上比递归较优。

    3）如果说记忆化搜索是从问题出发，寻找需要的条件计算，再综合求出答案，那么DP就是从最简单的条件开始计算，一步一步向变复杂，最后得出想要的值(这也是为什么要满足无后效性)

 

---

 

通常，找到了问题的状态转移方程后，就可以用记忆化搜索或递推来实现DP了

图解：

    最后，我们用一个图来总结一下暴力搜索、记忆化搜索和动态规划的异同。

 

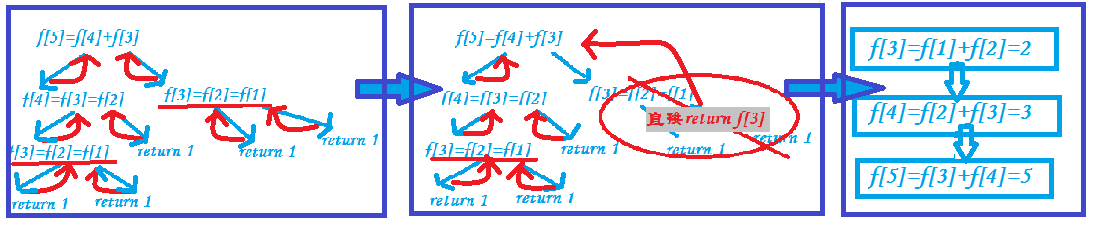
    施工完毕！