[OI学习笔记]最小生成树之Kruskal算法

Kruskal算法

    接着上次的写(本来打算过几天再更的...)

    上一篇博文写的是Prim算法，接着更Kruskal。

    还是上次的栗子：

    

 

 

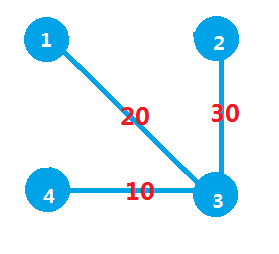
    如果说Prim是从点的角度考虑，那么Kruskal就是从边的角度考虑。

 

    Kruskal也是从贪心的角度解决的——从小到大连接每一条边，当我们选择一条边时，判断是否两个点是否在同一个联通块中，如果不在则选择该边。这样选择了n-1条边以后，所链接的就算是我们的MST了。

具体做法：

    1）快排

    2）按边权从小到大进行枚举

        1.判断这条边是否连接两个不在同一联通块的两点，如果是则连接

    3）循环n-1次

过程图解：

    我们擦掉栗子上的线，来手算一遍kruskal...

    1）什么都没有

    

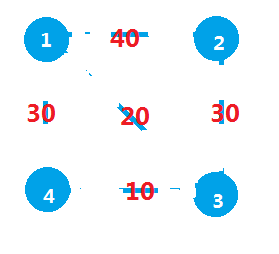
    2）当然是先选最短的啦

    

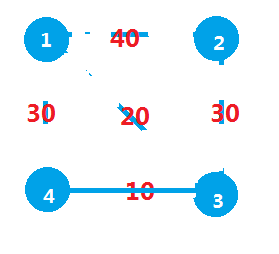
    3）第二短的20

    

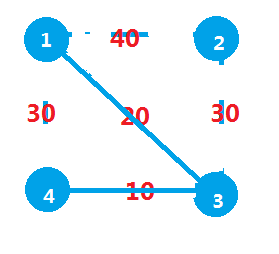
    3）这时，如果我们连接一根第三短的30，如果(1,4)被排在前面的话，我们发现，1和4已经在同一个并查集里面，不能连接

    

    4）所以我们继续选择(2,3)

    

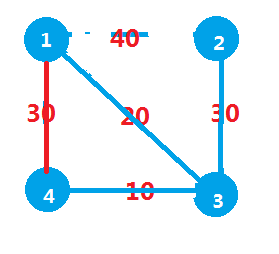
    5）完成，简单易懂.

    

    不过问题是代码实现。。。

    好吧，继续写。

    这里用邻接表，忘记说了上一篇因为数据量不大所以可以用邻接矩阵。

    以下是洛谷2330的代码（其实就是MST）

    （我可不是抄，我是看懂了之后再抄的）

代码

    

//最小生成树 Kruskal算法  洛谷2330
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
using namespace std;
struct road
{
    int A,B,V;
}R[10001];
int n,m,sz;
int to[20005],nex[20005],las[305];
void ins(int x,int y)
{
    sz++;to[sz]=y;nex[sz]=las[x];las[x]=sz;
    sz++;to[sz]=x;nex[sz]=las[y];las[y]=sz;
}
inline bool comp(const road &a,const road &b)
{
    return a.V<b.V;
}
void init()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=m;i++) 
        scanf("%d%d%d",&R[i].A,&R[i].B,&R[i].V);
}
bool check(int x,int y)
{
    bool u[305];
    memset(u,false,sizeof(u));
    int l[305],st=1,en=1;
    l[1]=x;u[x]=true;
    while (st<=en)
    {
        int tmp=l[st++];
        for (int i=las[tmp];i;i=nex[i])
        if (!u[to[i]])
        {
            u[to[i]]=true;
            l[++en]=to[i];
        }
    }
    return u[y]==false;
}
void solve(){
    int i,now=0;
    sort(R+1,R+1+m,comp);
    for(i=1;i<=m;i++)
        if(check(R[i].A,R[i].B))
        {
            ins(R[i].A,R[i].B);
            now++;
            if(now==n-1)
            {
                printf("%d %d\n",now,R[i].V);
                return;
            }
        }
}
int main()
{
    init();
    solve();
    return 0;
}

    最小生成树的内容就这么多，最后附上几道例题

    局域网

    修复公路

 

      火车运输(NOIP2013)

    星球大战

    源码会在近段时间贴出（再也不抄代码了...）