散列表
散列表的英文名叫"HASH TABLE",也叫哈希表或者HASH表。
散列表用的是数组支持按照下标随机访问的特点,其实就是一种数组的扩展,没有数据就没有散列表
例子:
比如说学校里面的每个学生都有编号,然后有89名学生去参加运动会,我们现在要做一个通过编号迅速找到学生信息,编号是这样的061101,06是年级,11是班级,01就是编号,这样我们就可以通过取每个编号的后两位数作为数组的下标把学生的信息存储下来。
这里的编号061101就是键或者关键字,这里的取每个编号的后两位数的过程叫作散列函数,这里的获取到的01也就是数组的下标,叫作散列值
下面是伪代码实现的散列函数(取编号的后两位)
int hash(String key) {
// 获取后两位字符
string lastTwoChars = key.substr(length-2, length);
// 将后两位字符转换为整数
int hashValue = convert lastTwoChas to int-type;
return hashValue;
}
散列表特点:
1.得到的散列值必须是非负数
2.如果key1=key2,那么func(key1)=func(key2)
3.如果key1≠key2,那么func(key1)≠func(key2)
第一点很好理解,因为数组下标是从0开始的,第二点也好理解,相同的值经过散列函数计算出来的值相同,第三点看起来也很好理解,但是其实大多数的散列函数都不能实现这个要求,就连业界有名的MD5,SHA等哈希算法,也无法避免散列冲突。
散列冲突是什么意思呢?
就是不同的值通过散列函数计算出来的散列值相同,也就是存储的数组的下标相同,那么就会带来冲突
那么解决散列冲突的方法一般有这么两种
1.开放寻址法
开放寻址法的核心思想是,如果出现了散列冲突,我们就重新探测一个空闲位置,将其插入, 那如何探测空闲位置呢?我们先来看这种线性探测的方法。
当我们往数组中插入数据时,发现该数组下标已经被占用,那么我们就依次往后面继续查找下标,直到找到空闲的数组下标然后将其插入。
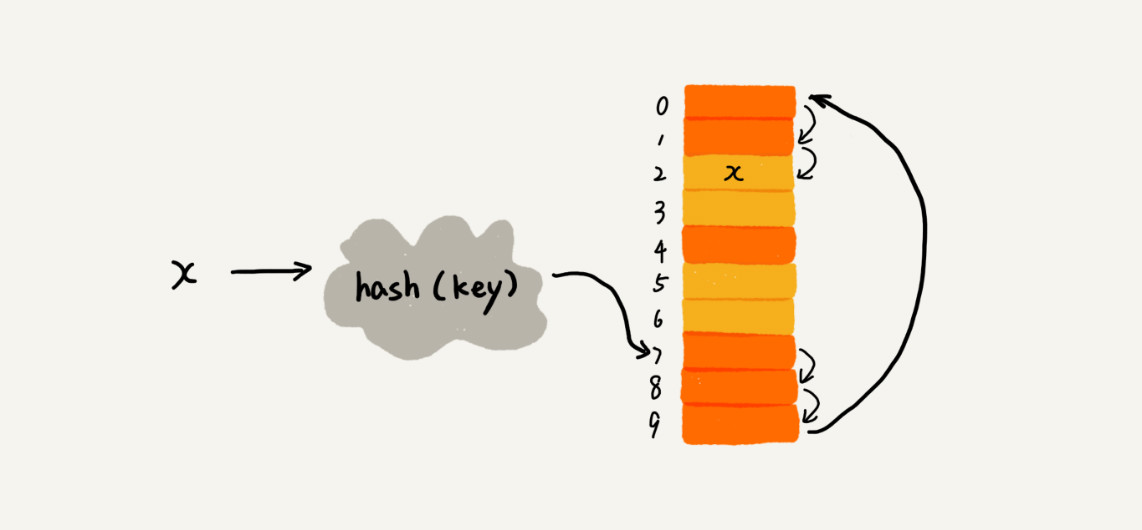
可以看到上图中x经过散列函数得到数组下标为7的位置,但是7已经被占用了,那么我们就继续往后查找,一直查到下标为2的位置是空闲的,那么我们就将其插入到这个位置。
这个时候当我们需要查找的时候就不能单纯的通过散列函数查找到对应的散列值来查找数据了,而是要在比对一下存储在该数组下标中的元素的值是否和需要查找的值一样
2.链表法
这个很好理解,就是把得出来相同散列值存在一个链表中
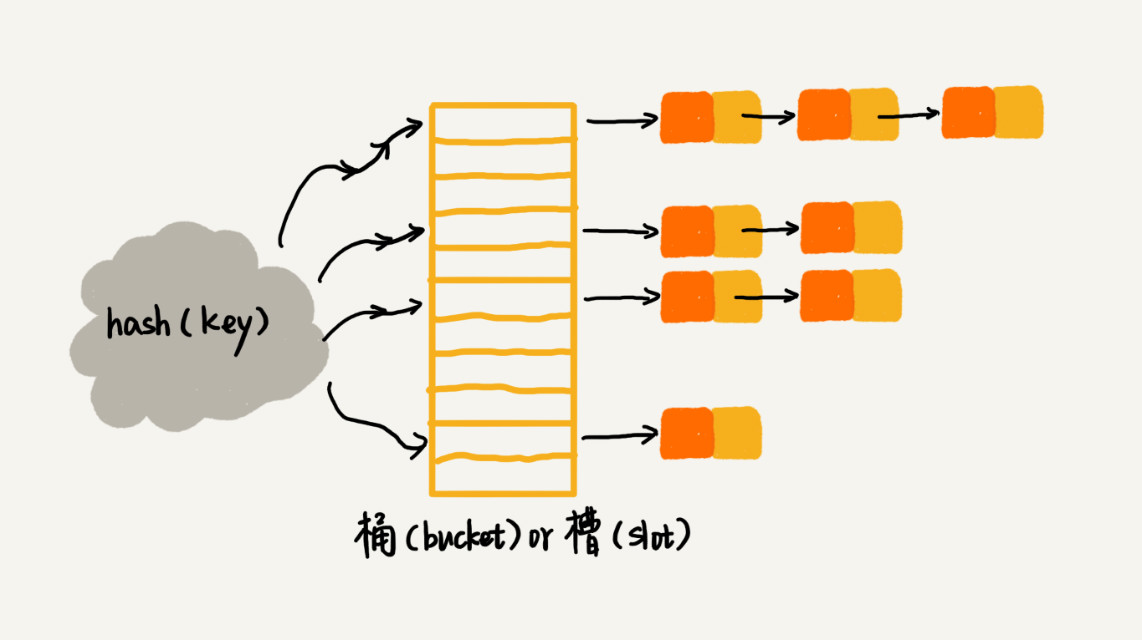
当插入的时候我们只需要通过散列函数插入到对应的链表中即可。





