《机器学习》第一次作业——第一至第三章学习记录和心得
第一章 模式识别基本概念
模式识别
概念：根据已有知识的表达或者说是函数映射，针对待识别模式，判别决策其所属的类别或者预测其对应的回归值，是一种推理过程，可划分为“分类”和“回归”两种形式。
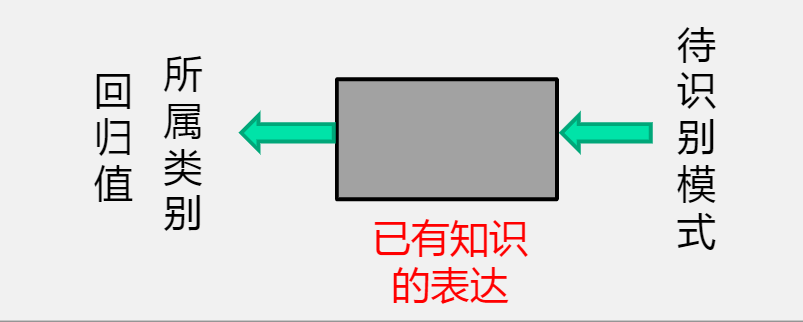
- 模型：已有知识的表达方式，即f(x)。
模式识别任务的模型通过机器学习获得。
机器学习
概念：利用训练样本，对目标函数进行学习优化（学习参数、模型结构等），得到理想的模型的过程。
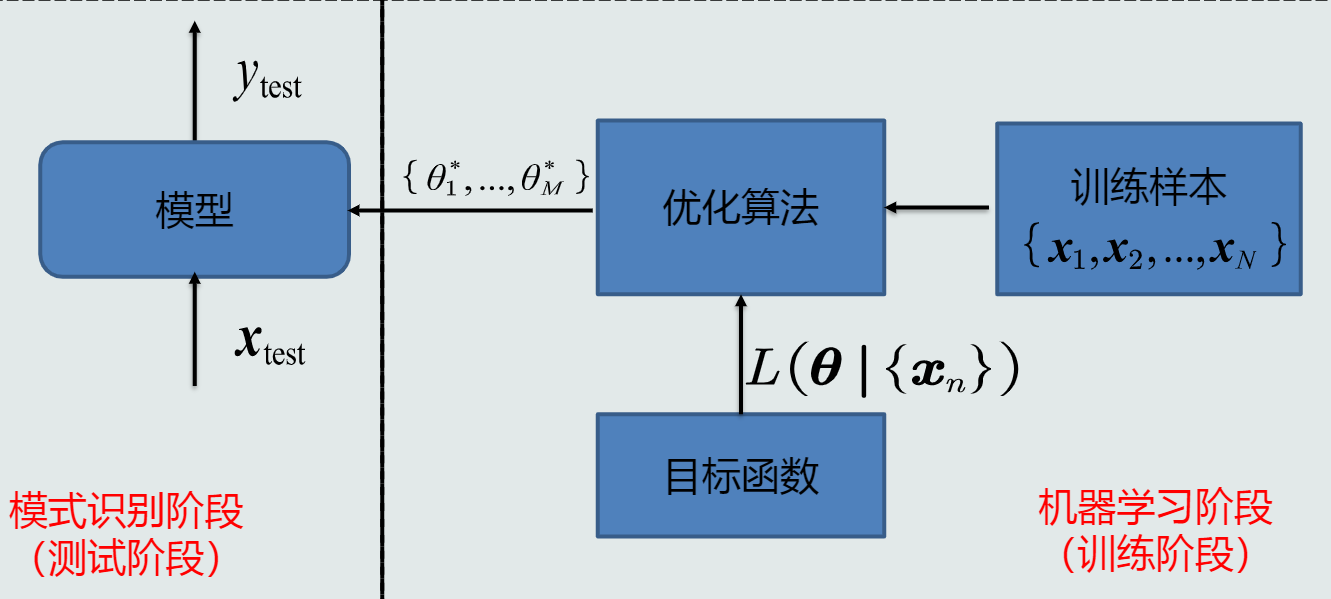
模型质量的评价
泛化能力：即训练得到的模型不仅要对训练样本有决策能力，也要对新的模式具有决策能力。
提升泛化能力的具体思路：不要过度训练，选择复杂度合适模型；通过调节正则系数，降低过拟合的程度
模型性能评估
- 留出法
随机划分：将数据集D随机划分为两个互斥的部分，其中一部分作为训练集S，另一部分用作测试集T。通常训练集和测试集的比例为70%：30%。
同时，训练集测试集的划分有两个注意事项：
1.尽可能保持数据分布的一致性。避免因数据划分过程引入的额外偏差而对最终结果产生影响。在分类任务中，保留类别比例的采样方法称为“分层采样”。
2.采用若干次随机划分避免单次使用留出法的不稳定性。 - K折交叉验证
将数据集D分为K个子集，取单个子集为测试集，其他K-1个为训练集，进行K次训练和测试，最终返回k个测试结果的均值。 - 留一验证
每次从数据集D中抽取一个样本作为测试集，剩余为训练集，每个样本测试一次，等同于K折交叉验证，K为数据及样本总数。
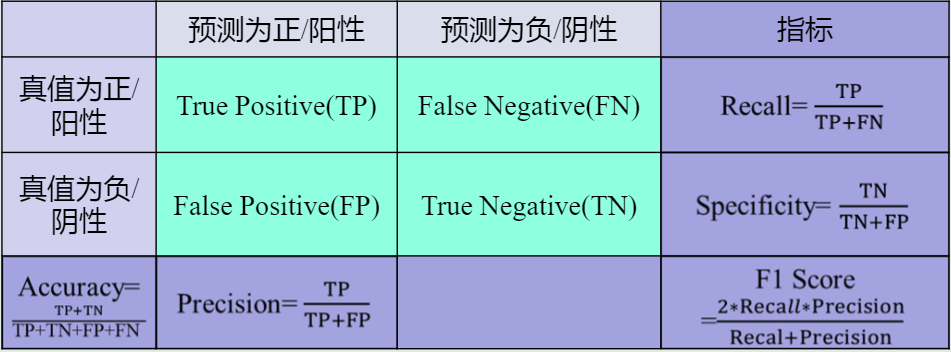
性能指标度量
准确度（Accuracy）、精度（Precision）、召回率（Recall）、曲线度量（）等
第二章 基于距离的分类器
MED分类器
基于欧式距离作为距离度量，没有考虑特征变化的不同及特征之间的相关性。
- 解决方法：使用特征白化去除特征变化的不同及特征之间的相关性。
欧氏距离进行特征白化后为马氏距离。
MICD分类器
基于马氏距离，经过特征正交白化，去除特征变化的不同及特征之间的相关性，缺陷是会选择方差较大的类。
第三章 贝叶斯决策与学习
第二章中，MICD分类器和MED分类器只考虑了距离，没有考虑数据的分布情况。为了更好的训练，我们引入了概率的观点。
- 贝叶斯规则：
已知先验概率和观测概率，模式𝒙属于类𝐶𝑖后验概率的计算公式为：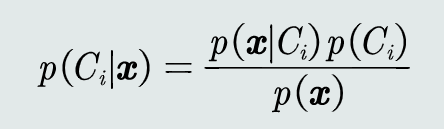
分类器
-
MAP分类器
将测试样本决策分类给后验概率最大的那个类。给定所有测试样本， MAP分类器选择后验概率最大的类，等于最小化平均概率误差，即最小化决策误差。 -
贝叶斯分类器
在MAP分类器基础上，加入决策风险因素，得到贝叶斯分类器，给定一个测试样本𝒙，贝叶斯分类器选择决策风险最小的类。
给定所有测试样本 {𝒙}，贝叶斯分类器的决策目标： 最小化期望损失。
监督式学习
参数化方法：给定表达式，学习表达函数中的参数。
最大似然估计
给定的𝑁个训练样本都是从𝑝(𝒙|𝜃)采样得到的、且都符合iid条件，则所有样本的联合概率密度为：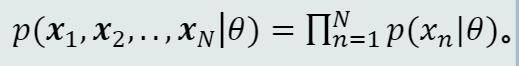
该函数称为似然函数
学习参数𝜃的目标函数：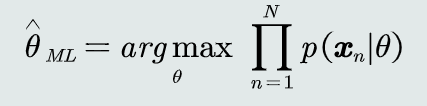
使得该似然函数最大
贝叶斯估计
给定参数𝜃分布的先验概率以及训练样本，估计参数θ分布的后验概率
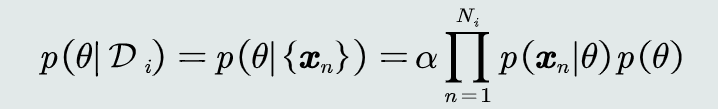
- 贝叶斯估计步骤
贝叶斯估计具有不断学习的能力。
非参数化方法
基于概率密度估计技术
KNN估计
给定𝒙，找到其对应的区域𝑅使其包含𝑘个训练样本，以此计算𝑝（𝒙） 。
优缺点：可以自适应的确定𝒙相关的区域𝑅的范围，但不是真正的概率密度表达，概率密度函数积分是 ∞ 而不是1。且容易受到噪声污染。
直方图方法
将特征空间分为m个格子，固定区域R的大小，计算𝒙属于哪个格子，计算所在格子的样本数。以此计算𝑝（𝒙）。
优缺点：减少由于噪声污染造成的估计误差，但是会受到区域交界处样本的影响，并且缺乏自适应能力。
核密度估计
以𝒙为中心固定带宽h，计算落入R的样本个数，以此计算𝑝（𝒙）。
优缺点：可以自适应确定R的代销，克服了KNN估计存在的噪声影响。但是要储存所有训练样本，耗费空间大。
