结对编程作业
相关链接
我的博客
队友博客
GitHub链接
| 姓名 | 工作 |
|---|---|
| 宋静慧 | 前端开发与后端交互 |
| 罗彤 | AI大比拼算法和生成拼图序列 |
2.1 原型设计
[2.1.1]设计说明
本次结对编程的原型设计采用了Axure设计组件,下面我们对使用Axure做出的原型图做出设计说明。(虽然其他的原型组件也不错,但是还是Axure好找到破解版,毕竟不要跟钱过不去嘛)
游戏主要流程如下:

整体的页面结构:

游戏整个风格比较黑暗,比较有密室逃脱的感觉,整个游戏分为开始界面,游戏界面这两个主要界面。
-
开始界面
我们为了增加游戏可玩性,决定在开始界面添加3×3、4×4和5×5三种游戏难度的直达游戏按钮,点击直达相应的难度游戏界面,以及当玩家想要挑战更高难度时,可以点击华容道,自行选择更高的阶数。下面还有一个按钮则是往次得分,显示不同难度的历史记录。

-
游戏界面
游戏界面主要分为三个部分,按钮部分、计数部分和滑动拼图部分。

拼图部分由原图和图片切块的游戏区组成,在图片切块区移动图片切块,直至还原图片。
计数部分则有两个数据,时间和步数,通过时间和步数的计算来达到游戏一个紧张刺激的感觉。

按钮部分的内容就比较多一点,主要有返回、重来、下一步和帮助这四个按钮
返回按钮则返回开始界面,重新选择游戏难度或者查看往次得分;重来按钮是用于将图片切块部分还原到最开始的样子,同时将时间和步数均设为0,重新开始;下一步是为了增加游戏可玩性,给玩家提示;帮助按钮则是直接移动图片切块,将图片还原。

- 数字华容道
数字华容道的设计主要是为了增加游戏难度,毕竟在高阶的情况下,图片不好辨认,此时用数字来标记可以使用户获得更好的体验。

数字华容道高阶的界面如下,显示从1-n*n的数字块,随机去掉一块。

- 往次得分
往次得分主要显示了不同难度等级过去五次解出答案的用时和步数,主要是33,44和5*5难度的记录,点击返回可以返回开始界面。

[2.1.2]结对讨论
描述结对的过程,提供非摆拍的两人在讨论、细化和使用专用原型模型工具时的结对照片。

[2.1.3]遇到的困难及解决方法:
- 困难描述
我们之前都没有怎么接触过原型设计,特别是关于游戏的原型设计,和普通app或者软件的简洁为主不同,游戏原型设计要饱
满,不能让界面显得空旷简单,除此之外,Axure的使用对于我们来说也是一个难题。 - 解决尝试
我们为了熟悉关于游戏的原型设计,在几天内下载了许多相关的小游戏app以及PC端小游戏,体验相关的原型设计与游戏逻辑。 - 是否解决
我们结合多个游戏的游戏场景与游戏体验画出流程图,然后根据流程图设计滑动拼图小游戏。 - 有何收获
在这次的原型设计中,我们学会了使用Axure,同时,我们也学会如何快速的体验一款软件,了解其相关信息与设计逻辑,了解游戏设计与生活办公类软件设计的不同。
2.2 AI与原型设计实现
[2.2.1]代码实现思路:
一、网络接口的使用
- 1.api接口地址
http://47.102.118.1:8089/ - 2.获取当日赛题列表
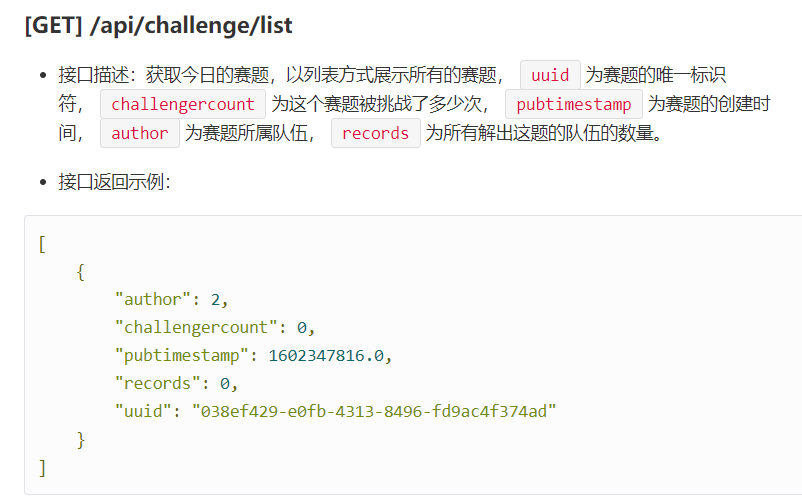
# 获取赛题,以列表方式展示所有的赛题
def get_question(url_):
response = requests.get(url=url_)
resp = json.loads(response.text)
return resp
- 3.获取赛题的解题记录
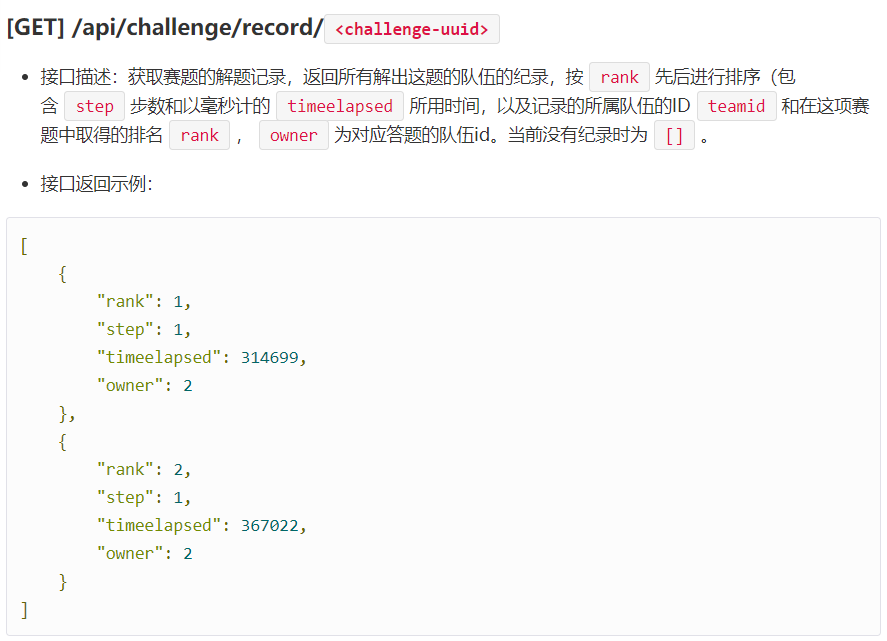
# 获取赛题的解题记录,返回所有解出这题的队伍的纪录(列表)
# 按rank先后来排序,owner为队伍id
def get_record(url_):
response = requests.get(url=url_)
resp = json.loads(response.text)
return resp
- 4.创建赛题

# 创建赛题,用token作为权限验证,提供队伍的teamid和赛题数据data。创建成功返回赛题标识符uuid。
# data中letter表示赛题的对应字母、exclude表示当前哪个位置的图片被删去作为空格,challenge为游戏地图,
# step为强制交换的步数(0<=X<=20),swap为强制交换的图片(从左到右从上到下编号1-9)
def post_create(url_, teamid, letter, exclude, challenge, step, swap, token):
url = url_
question = {"teamid": teamid,
"data": {
"letter": letter,
"exclude": exclude,
"challenge": challenge,
"step": step,
"swap": swap
},
"token": token}
response = requests.post(url=url_, json=question)
resp = json.loads(response.text)
return resp
- 5.挑战赛题的接口
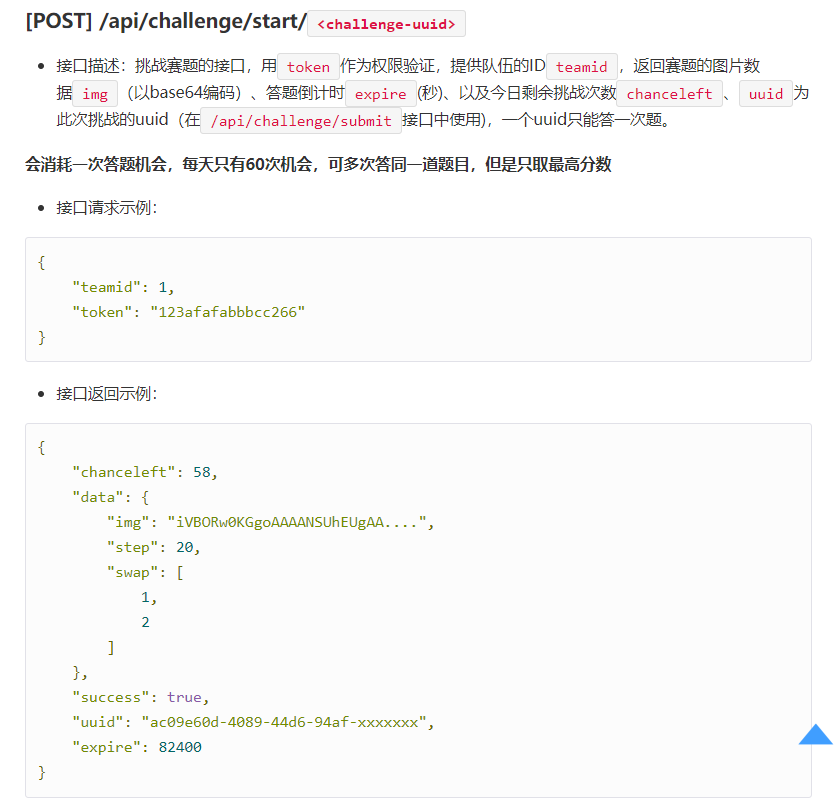
# 挑战赛题的接口
def post_challenge(url_, teamid, token):
# url = url_
data = {"teamid": teamid,
"token": token
}
response = requests.post(url=url_, json=data)
resp = json.loads(response.text)
return resp
- 6.提交赛题答案的接口

# 提交赛题答案的接口
def post_submit(url_, uuid, teamid, token, operations, swap):
# url = url_
data = {"uuid": uuid,
"teamid": teamid,
"token": token,
"answer": {
"operations": operations,
"swap": swap
}
}
response = requests.post(url=url_, json=data)
resp = json.loads(response.text)
return resp
- 7.从高到低返回排行榜
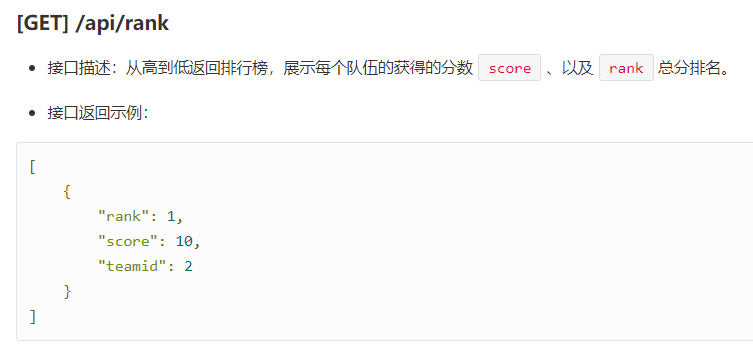
# 从高到低返回排行榜,展示每个队伍的获得的分数score、以及rank总分排名
def get_rank(url_):
response = requests.get(url=url_)
resp = json.loads(response.text)
return resp
- 8.获取指定队伍的信息
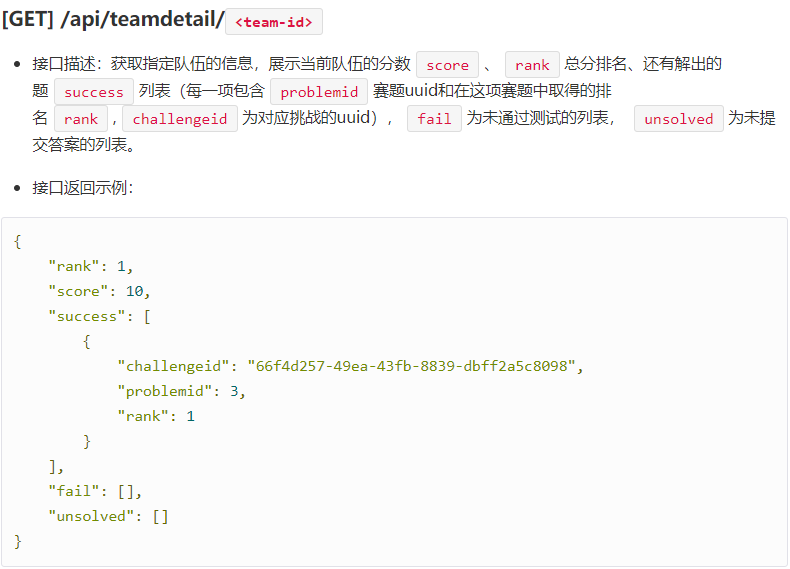
# 获取指定队伍的信息,展示当前队伍的分数score、rank总分排名、还有解出的题success列表
def get_teamdetail(url_):
response = requests.get(url=url_)
resp = json.loads(response.text)
return resp
- 9.获取还未通过的题目
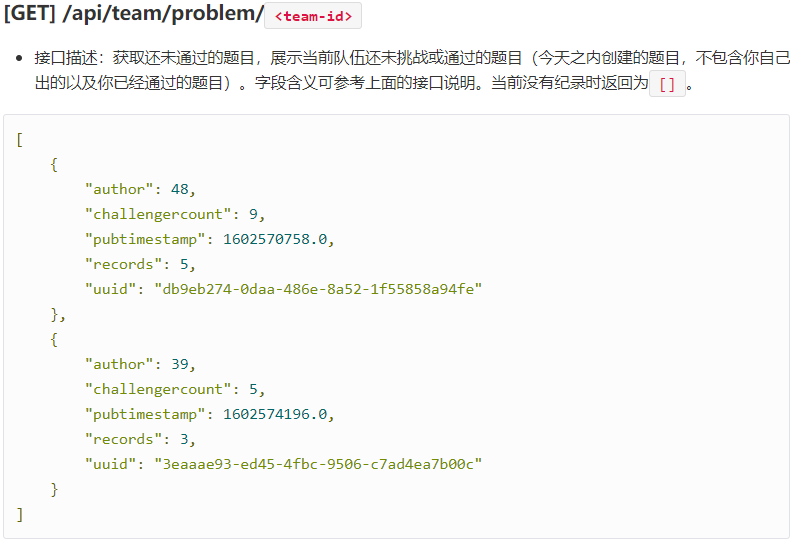
# 获取还未通过的题目,展示当前队伍还未挑战或通过的题目(不包括自己出的)
def get_problem(url_):
response = requests.get(url=url_)
resp = json.loads(response.text)
return resp
二、代码组织与内部实现设计
小游戏类图

三、算法的关键与关键实现部分流程图
- 1.求解8数码问题
数字华容道的算法当然是8数码问题的求解了,我们的核心求解算法使用的是IDAstar(迭代加深Astar)算法,结合A*算法的核心思想:f(n)=g(n)+h(n),以及剪枝操作,从而在短时间内求出最优解。
具体求解8数码问题的代码参考了知乎上的一篇文章:Astar、IDAstar入门:八数码问题 - 2.图片匹配
AI大比拼的题目是数字华容道的升级版————图片华容道,因此在求解8数码问题之前需要先根据题目给出的图片到原图库里寻找对应的原图,才能知道8数码问题的初始状态、初始白块位置和目标状态,进而应用8数码求解代码来解题。
由于题目给出的是初始乱序图的base64编码,因此需要先讲base64编码转为图片,代码如下:(其中,Image是PIL库中的一个类)
img = base64.b64decode(img_base64) # base64编码转字符串
img = BytesIO(img) # 字符串转字节流
pic = Image.open(img) # 以图片形式打开img
图片切片及保存的代码参照了网上的一片文章:用Python发一个高逼格的朋友圈
(没错,就是教你用python把一张图片切成九张,然后发在朋友圈里装*)
- 3.强制交换&自由交换
由于游戏规则中有强制交换,因此一般的搜索算法难以得到最短路径。强制交换造成无解时,一个好的自由交换也能够减小路径长度。但在这里,我们使用的是最简单的方法,即:①把强制交换后的状态当做一个新问题来求解;②自由交换时使用manhattan距离总和来作为估计代价,选择使得manhattan距离总和最小的交换方式进行自由交换。因此对于需要强制交换的样例,我们的算法得到的路径一般都比较长Orz - 关键实现部分流程图

四、部分代码解释
- 0.滑动拼图的滑动动画
def slide_animation(blank_x, blank_y, current_list, direction, img_area, rect, seg_width, size, pic, steps):
move_x, move_y, check = 0, 0, 0
if direction == UP:
move_x, move_y, check = blank_x, blank_y-1, 1
elif direction == DOWN:
move_x, move_y, check = blank_x, blank_y+1, 1
elif direction == LEFT:
move_x, move_y, check = blank_x-1, blank_y, 1
elif direction == RIGHT:
move_x, move_y, check = blank_x+1, blank_y, 1
if check == 0:
return move_x, move_y, check, steps
base_surf = screen.copy() # 复制一个新的窗口对象
# 绘制空白区(这时候有2块空白区域)
num2 = move_x+move_y*size
steps = steps+1
pygame.draw.rect(base_surf, white, (img_area[num2], (seg_width, seg_width)))
base_surf = base_surf.copy()
my_font = pygame.font.Font('3.ttf', int(200 // size))
# 绘制滑动效果
for i in range(0, seg_width, 15): # 15步长偏移速度,每次循环后方块的位置向指定方向移动
screen.blit(base_surf, (0, 0))
if direction == UP:
screen.blit(pic, (img_area[num2][0], img_area[num2][1]+i), rect[current_list[num2]]) #x不动,y轴向上偏移
if direction == DOWN:
screen.blit(pic, (img_area[num2][0], img_area[num2][1]-i), rect[current_list[num2]]) # x不动,y轴向下偏移
if direction == LEFT:
screen.blit(pic, (img_area[num2][0]+i, img_area[num2][1]), rect[current_list[num2]]) # y不动,x轴向右偏移
if direction == RIGHT:
screen.blit(pic, (img_area[num2][0]-i, img_area[num2][1]), rect[current_list[num2]]) # y不动,x轴向左偏移
pygame.display.update()
pygame.time.delay(FPS)
return move_x, move_y, check, steps
- 1.图片匹配
这部分共有五个函数,fill_image、cut_image、save_images、original_partition、img_match,在知乎上看到的代码的基础上稍加改动,就是前三个函数了。先上代码↓
# 将图片填充为正方形
def fill_image(image):
width, height = image.size
# 选取长和宽中较大值作为新图片的
new_image_length = width if width > height else height
# 生成新图片[白底]
new_image = Image.new(image.mode, (new_image_length, new_image_length), color='white')
# 将之前的图粘贴在新图上,居中
if width > height: # 原图宽大于高,则填充图片的竖直维度
new_image.paste(image, (0, int((new_image_length - height) / 2))) # (x,y)二元组表示粘贴上图相对下图的起始位置
else:
new_image.paste(image, (int((new_image_length - width) / 2), 0))
return new_image
# 切图(n * n)
def cut_image(image, n):
width, height = image.size
item_width = int(width / n)
box_list = []
# (left, upper, right, lower)
for i in range(0, n):
for j in range(0, n):
# print((i*item_width,j*item_width,(i+1)*item_width,(j+1)*item_width))
box = (j * item_width, i * item_width, (j + 1) * item_width, (i + 1) * item_width)
# box = np.asarray(box) # 将切片转换为numpy矩阵
box_list.append(box)
# image_list = [image.crop(box) for box in box_list]
# 保存为10*10像素
image_list = [image.crop(box).resize((10, 10)) for box in box_list]
return image_list # 返回numpy矩阵列表
# 保存
def save_images(image_list, content):
index = 0
for image in image_list:
image.save(content + '/' + str(index) + '.jpg', 'JPEG')
index += 1
# 输入一个文件名称(与原图文件名一样,不包括后缀),将图像切片并新建一个与图像文件名相同的文件夹(如果该文件夹不存在的话),并将切片保存在其中
# 注意,需要在当前目录下有存放各原图切片结果文件夹的tiles文件夹,且要有存放完整原图的original_img文件夹
# 所有图片均为jpg格式
def original_partition(dir):
dirs = './tiles' # 当前目录下的tiles目录,用于存放所有原图的切片结果
file_path1 = "original_img" # 当前目录下的original_img文件夹
file_path2 = dir + '.jpg' # 输入original_img文件夹中的jpg文件全名(dir不包括.jpg后缀)
file_path = os.path.join(file_path1, file_path2) # 组合成完整的源文件(待切片的图片)路径
image = Image.open(file_path) # 打开图片
# image.show()
image = fill_image(image) # 将图片填充为方形
image_list = cut_image(image, 3) # 切割图片(3*3)
# 在tiles文件夹里再建一个文件夹,存放一张原图的所有切片,文件夹的名字与原图文件名(不包括后缀)一样
dir_path = os.path.join(dirs, dir) # 组合成完整的目标文件夹路径
# 判断文件夹是否存在,若不存在则创建目标文件夹
if not os.path.exists(dir_path):
os.makedirs(dir_path)
save_images(image_list, dir_path) # 保存切片结果
# 从接口中接收测试数据,输出与乱序图匹配的原图文件名(不包括.jpg后缀)以及乱序图相对于原图的位置状态
# 注意,当前文件夹下需要有1.存放所有原图切片的文件夹tiles;2.chaos文件夹;3.chaos文件夹中还需要有discrete文件夹
# 完整的乱序图保存在chaos文件夹下,命名为integral.jpg
# 切片的乱序图保存在discrete文件夹中
def img_match(img_base64):
img = base64.b64decode(img_base64) # base64编码转字符串
img = BytesIO(img) # 字符串转字节流
pic = Image.open(img) # 以图片形式打开img
# 将读取的测试图片保存到本地,同目录下的chaos文件夹中,并命名为integral.jpg
pic.save('./chaos/integral.jpg', 'JPEG')
# 将原图切分为3*3片,存入img_list列表,并将切片保存到同目录./chaos/discrete文件夹中
img_list = cut_image(pic, 3)
save_images(img_list, './chaos/discrete')
ls_chaos = [] # 存放乱序切片的numpy矩阵的列表
for root, dirs, files in os.walk("./chaos/discrete"): # 遍历discrete文件夹
for file in files: # 处理该文件夹里的所有文件
p = Image.open(os.path.join(root, file)) # 合成绝对路径,并打开图像
p = np.asarray(p) # 图像转矩阵
ls_chaos.append(p) # 将得到的矩阵存入列表
stat = [-1, -1, -1, -1, -1, -1, -1, -1, -1] # 存放乱序图片的状态,-1代表白块,0~8代表该切片是处于原图中的哪一位置
dir_path = "./tiles_10"
# 遍历同目录中./tiles文件夹中的所有文件夹
for root, dirs, files in os.walk(dir_path):
for dir in dirs:
# k代表状态列表下标,cnt记录当前已匹配上的切片数
k, cnt = 0, 0
# tar_stat列表存放目标状态,由于不同原图之间可能存在完全一样的切片,会影响tar_stat的最终结果
# 因此每次与新的一张原图比较前,将tar_stat初始化为全-1
tar_stat = [-1, -1, -1, -1, -1, -1, -1, -1, -1]
# 从ls_chaos列表(即乱序切片的numpy矩阵列表)中,逐个与原图库中的切片比较
for i in ls_chaos:
# index用于指示乱序的切片在原图的哪一位置
index = 0
# 遍历存放原图切片的文件夹中的所有文件(即,原图切片)
for root, dirs, files in os.walk(os.path.join(dir_path, dir)):
for j in files:
# 用os.path.join()拼接出文件的绝对路径,然后打开该文件(图片)
j = Image.open(os.path.join(root, j))
j = np.asarray(j) # 将原图切片转换为numpy矩阵
if (i == j).all(): # 判断两个矩阵是否完全相同
stat[k] = index
tar_stat[index] = index
cnt += 1
break
index += 1
k += 1
# 若已有8个切片匹配上则说明匹配到了原图
if cnt > 7:
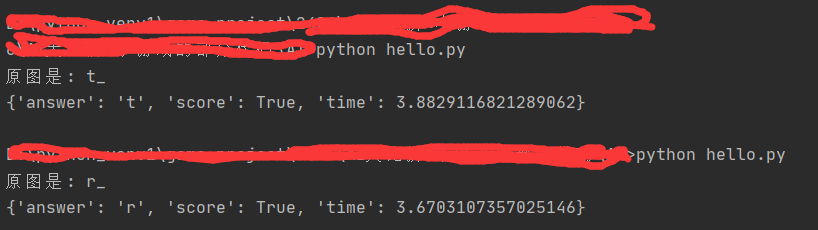
print("原图是:", dir) # 打印原图名称
break
if cnt <8:
print("没找到原图QAQ")
# 遍历初始状态列表,获得白块的初始位置
for i in range(len(stat)):
if stat[i] < 0:
blank = i
break
# 返回初始状态(列表)、空白块位置、目标状态(列表)
return stat, blank, tar_stat
fill_image、cut_image、save_images三个函数参照知乎上搬过来的代码,这里不多说了。
original_partition函数负责将原图文件夹original_img中存放的完整原图切片,并保存在tiles_10文件夹中,相关文件夹中的文件情况见下图:
original_img:

tiles_10:
tiles_10/a_:
img_match函数则是将从接口中获取的图片base64编码转为图片,并将其切片,存放在chaos文件夹中,文件情况如下:

将初始乱序图切片并保存后,使用四重循环在原图文件夹(original_img)中依次寻找与乱序图匹配的图片,由于乱序图中一块变成了白色,故乱序图应有8块能够与原图匹配上。在匹配的同时,也用两个列表stat、tar_stat分别记录初始状态和目标状态,用一个变量blank记录初始白块位置(注意,在本算法中,9个图片的编号是从0-8,而测试中是从1-9,故在主函数中还要加一步转换操作,这里就没展示出来了)。
- 2.判断当前状态是否可解
判断N 数码是否有解
这篇博客已经很详细地讲解了如何判断8数码问题的可解性,甚至进行了推广。总的而言,当阶数为奇数时,可解性仅与初末状态逆序对的奇偶性有关,同奇同偶则可解;而当阶数为偶数时,可解性不仅与初末状态逆序对的奇偶有关,还跟空白块的初末状态有关,具体讲解可参考上面这篇博客。
逆序对数的求解,最简单直接的方法就是两重循环,但是由于数据结构课上做过求逆序对数的题目,使用的是归并排序的方法,因此我们在这里使用了基于归并排序的逆序对数计数算法(尽管当初用C语言打出来了,但是用python语言翻译之后还是写出了不少bug……主要还是不了解python的许多特性,比如深拷贝、浅拷贝、for循环函数的用法等……跪了Orz)。
由于求解逆序对数的代码较长,这里仅展示基于该函数来判断是否有解的函数Judge_even,也即,判断逆序对数是否为偶数。
# 判断列表中逆序对数的奇偶,若为偶,返回True
# 计算逆序对数时,不算空白块
def Judge_even(listA):
n = len(listA)
# inverse_number函数会进行归并排序,破坏原列表,故先拷贝一份
tmp = copy.deepcopy(listA)
for i in range(n):
if tmp[i] < 0:
del tmp[i]
n -= 1
break
cnt = inverse_number(tmp, n)
if (cnt % 2) == 0:
return True
else:
return False
- 3.强制交换&自由交换
在我们的代码中,将IDAstar和强制交换算法写在了一个类IDAstar中(因为参考的IDAstar算法函数就是用c++的类写的,被迫学习python中类的用法Orz……),因此函数中的self代表一个IDAstar类的实例本身,代码如下:
# 在当前状态stat进行强制交换,若强制交换导致无解,则紧接着进行一次自由交换
# 返回强制交换的方案
def forced_exchange(self, stat):
# 交换两个块
tmp0 = copy.deepcopy(stat)
tmp0[self.swap_scheme[0]], tmp0[self.swap_scheme[1]] = tmp0[self.swap_scheme[1]], tmp0[self.swap_scheme[0]]
# 若最初的强制交换不会造成无解,则返回
if Judge_even(tmp0) == self.solvable:
return self.swap_scheme
# 否则,进行自由交换
else:
# 先要强制交换,在强制交换的基础上自由交换
stat[self.swap_scheme[0]], stat[self.swap_scheme[1]] = stat[self.swap_scheme[1]], stat[self.swap_scheme[0]]
# 双重循环,遍历可自由交换出的所有状态
for i in range(8):
for j in range(i+1, 9):
tmp = copy.deepcopy(tmp0)
tmp[i], tmp[j] = tmp[j], tmp[i]
if Judge_even(tmp) == self.solvable:
for k in range(len(tmp)):
if tmp[k] < 0:
break
tmp_board = Board(tmp, k)
cost_h = tmp_board.cost
# 以cost_h为键,交换方案为值,可能会有多个方案的cost_h相同的情况,但字典中只记录一个
self.swap_record[cost_h] = [i, j]
m = min(self.swap_record) # 找到最小的代价
self.swap_scheme = copy.deepcopy(self.swap_record[m])
return self.swap_scheme # 返回最小代价对应的交换方案
大致流程见上文的算法流程图。在强制交换&自由交换(fored_exchange函数)里,我被深拷贝浅拷贝给整蒙了,找了半天的bug,最后发现是python的赋值方式跟c的不一样,吐血。
对于自由交换,我的做法是用一次两重循环遍历可自由交换出的所有状态,判断交换而得的一个新状态是否可解,若可解则计算该状态的估计代价(计算总的manhattan距离),并且以估计代价为键、交换方式为值加入到字典swap_record中。当遍历完所有可能的情况后,在字典中选择键最小的元素,得到相应的交换方式,即为自由交换的结果。
-
- IDAstar算法
具体代码较长,具体见github连接
其中的Board类和IDAstar类即是与此相关的两段代码,当然,也可参考上文提到的知乎文章Astar、IDAstar入门:八数码问题
应当注意的是,强制交换的时机是:第n步(从0计数)之前、第n-1步之后开始强制交换,经大佬点拨后,我才知道即使强制交换或自由交换之后直接到达目标状态,还是需要在求解路径中再增加一步,否则算错(在测试中,每50次左右的测试,都会有一次是False,在改完这个bug后,连续测试了几百次,没有报错)。
- IDAstar算法
五、性能分析与改进
在8数码问题的求解算法方面,我们没有什么改进(开玩笑,除了bfs、dfs、Astar算法,其他都不懂的菜鸡,还改大佬的代码,别把自己作死了叭)。
因此,我主要是在图片匹配方面对代码进行了优化,在优化之前,所有原图、初始乱序图都是直接切成九片,匹配速度较慢,测试结果、性能分析如下:


可见,如果直接用原图切片(300×300像素)进行匹配,速度很慢。
经大佬点拨(你两次说的大佬……是同一个?是的……233),可以将图片调整为10*10像素大小,可以大大缩短匹配时间,并且还能提高匹配成功率(这是我没想到的,未优化之前,每二十次左右的测试,就会有一次匹配不上原图,优化后居然就没这问题了emmmmmm)。
优化后的测试结果、性能分析如下:
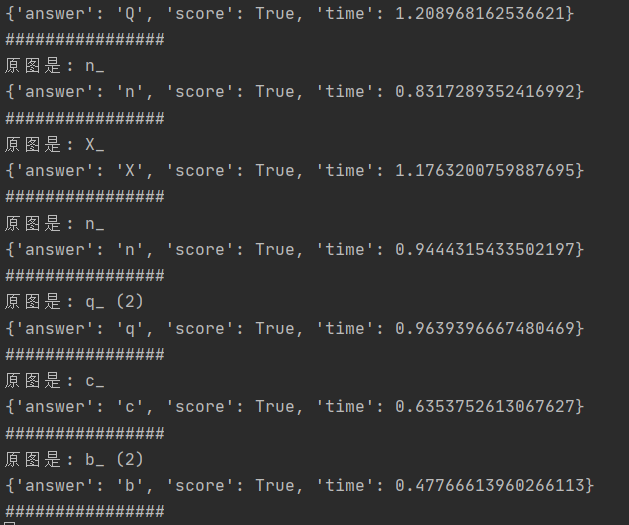

可以看到,程序运行时间大幅提高,其中8数码求解时间很短,没有显示。
[2.2.2]贴出Github的代码签入记录,合理记录commit信息。

[2.2.3]遇到的代码模块异常或结对困难及解决方法:
-
困难描述
1.不了解PIL库的使用,不会图片操作;
2.由于不了解python特性而没有意识到的浅拷贝、深拷贝、for函数的功能,导致代码的bug喷涌而出;
3.对于ai大比拼的规则不清晰,导致生成错误结果。 -
解决尝试
面向百度的递归迭代学习。
1.百度学习PIL库的使用,学习Image类及其相关函数(resize、crop等)的使用;
2.百度学习相关特性,了解copy库,使用copy.deepcopy函数完成深拷贝;
3.了解for range函数的功能;
4.经自己探索、大佬解答,摸清游戏规则。 -
是否解决
全部解决(那是当然…………,不然ai大比拼就炸了,虽说本来算法求出来的路径普遍较长,也算是炸了Orz)。 -
有何收获
不要轻易肯定自己的代码不会有bug,bug是补不完的嘤嘤嘤;
作为新时代的新青年,提高自己面向Internet解决问题的能力太重要了,我还需要努力;
大佬带的感觉一定很爽。
[2.2.4]评价你的队友。
- 值得学习的地方
做事认真,很负责,做事有规划 - 需要改进的地方
感觉都挺好的,没什么需要改进的。
[2.2.5]结对作业的PSP和学习进度条
- PSP表格
| Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|
| Planning(计划) | 60 | 60 |
| Estimate(估计时间) | 30 | 30 |
| Development(开发) | 2950 | 3890 |
| Analysis(需求分析(包括学习新技术)) | 1200 | 1450 |
| Design Spec(生成设计文档) | 120 | 255 |
| Design Review(设计复审) | 30 | 60 |
| Coding Standard(代码规范 ) | 30 | 45 |
| Design(具体设计) | 280 | 265 |
| Coding(具体编码) | 1200 | 1500 |
| Code Review(代码复审) | 90 | 135 |
| Test(测试(自我测试,修改代码,提交修改)) | 120 | 180 |
| Reporting(报告) | 120 | 280 |
| Test Report(测试报告) | 30 | 45 |
| Size Measurement(计算工作量) | 30 | 30 |
| Postmortem & Process Improvement Plan(事后总结, 并提出过程改进计划) | 60 | 50 |
| Total(合计) | 3130 | 4230 |
- 学习进度条
| 第N周 | 新增代码(行) | 累计代码(行) | 本周学习耗时(h) | 累计学习耗时(h) | 重要成长 |
|---|---|---|---|---|---|
| 1 | 100 | 100 | 10 | 10 | 1.主要把作业捋一遍,确定要做的部分的相关知识,进行学习 2.了解了html、css和JavaScript的相关知识,以便后面小游戏的原型实现 |
| 2 | 479 | 579 | 13 | 23 | 1.着手进行微信小程序的设计,包括设计原型图,学习小程序开发知识 |
| 3 | 593 | 1172 | 15 | 38 | 1.逐步完成小程序功能,在开发过程中根据图片效果美化图片风格,同时找开发bug |
| 4 | 587 | 1759 | 21 | 59 | 1.着手pygame小游戏开发,重新设计原型图,将原型图通过pygame语言实现 测试并修复小游戏中的bug |
| 5 | 218 | 1977 | 14 | 73 | 1.bug修复,增加新功 |



