POJ3233 Matrix Power Series (等比矩阵求和)

题意：：求等比矩阵和：S = A + A² + A³ + … + A^k

参考巨佬们的经典算法（ 接近模板 ）

:::构造矩阵  E为单位矩阵

 

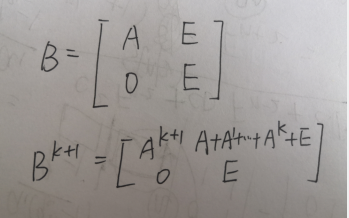
 看不明白的可以手模一下，

答案就是 右上角子矩阵减一个同阶单位矩阵

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn=65;

int n,MOD,k;
struct mat
{
    int a[maxn][maxn];
    mat(){
        memset(a,0,sizeof(a));
    }
};
mat mul(mat x,mat y)
{
    mat res;
    for(int i=0;i<n;i++)
    {
        for(int j=0;j<n;j++)
        {
            for(int k=0;k<n;k++)
            {
                res.a[i][j]=(res.a[i][j]+x.a[i][k]*y.a[k][j]%MOD)%MOD;
            }
        }
    }
    return res;
}
mat qpow(mat x,int p)
{
    mat res;
    for(int i=0;i<n;i++){
        res.a[i][i]=1;
    }
    while(p)
    {
        if(p&1){
            res=mul(res,x);
        }
        x=mul(x,x);
        p>>=1;
    }
    return res;
}
int main()
{
    scanf("%d%d%d",&n,&k,&MOD);
    mat ans;
    for(int i=0;i<n;i++){
        for(int j=0;j<n;j++){
            scanf("%d",&ans.a[i][j]);
            ans.a[i][j]%=MOD;
        }
    }
    for(int i=n;i<(n<<1);i++){
        ans.a[i-n][i]=ans.a[i][i]=1;
    }
    n=n<<1;
    ans=qpow(ans,k+1);
    n=n>>1;
    for(int i=0;i<n;i++)
    {
        ans.a[i][i+n]=(ans.a[i][i+n]-1+MOD)%MOD;
    }
    for(int i=0;i<n;i++)
    {
        for(int j=n;j<(n<<1);j++)
        {
            printf("%d ",ans.a[i][j]);
        }
        printf("\n");
    }
    return 0;
}

 

 矩阵快速幂+二分

S = A + A² + A³ + … + A^k

对于整数而言：：

n为偶数时：：S[n]=(a^(n/2)+1)*S[n/2]

n为奇数时：：S[n]=(a^(n/2+1)+1)*S[n/2]+(a^(n/2)+1);

对于矩阵也同样适用 ，当n==0时 S为单位矩阵；

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn=65;

int n,MOD,k;
struct mat
{
    int a[maxn][maxn];
    mat(){
        memset(a,0,sizeof(a));
    }
};
mat mul(mat x,mat y)
{
    mat res;
    for(int i=0;i<n;i++){
        for(int j=0;j<n;j++){
            for(int k=0;k<n;k++){
                res.a[i][j]=(res.a[i][j]+x.a[i][k]*y.a[k][j]%MOD)%MOD;
            }
        }
    }return res;
}
mat add(mat x,mat y)
{
    mat res;
    for(int i=0;i<n;i++){
        for(int j=0;j<n;j++){
            res.a[i][j]=(res.a[i][j]+x.a[i][j]+y.a[i][j])%MOD;
        }
    }
    return res;
}
mat qpow(mat x,int p)
{
    mat res;
    for(int i=0;i<n;i++){
        res.a[i][i]=1;
    }
    while(p){
        if(p&1){
            res=mul(res,x);
        }
        x=mul(x,x);
        p>>=1;
    }
    return res;
}
mat solve(mat x,int k)
{
    if(k==1){
        return x;
    }
    mat t=solve(x,k/2);
    if(k&1){
        mat res=qpow(x,k/2+1);
        t=add(add(mul(res,t),t),res);
    }
    else{
        mat res=qpow(x,k/2);
        t=add(mul(res,t),t);
    }
    return t;
}

int main()
{
    scanf("%d%d%d",&n,&k,&MOD);
    mat ans;
    for(int i=0;i<n;i++){
        for(int j=0;j<n;j++){
            scanf("%d",&ans.a[i][j]);
            ans.a[i][j]%=MOD;
        }
    }
    ans=solve(ans,k);
    for(int i=0;i<n;i++){
        for(int j=0;j<n;j++){
            printf("%d ",ans.a[i][j]);
        }printf("\n");
    }
    return 0;
}