HDU6395 矩阵分块快速幂

 

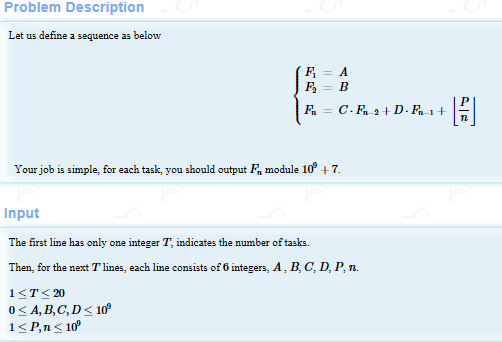
 一眼望去就是矩阵快速幂，但是题目所给你的是非线性递推式，因此要想办法构建矩阵求解；

由这个⌊P/n⌋可知在某一区间内值是相等因此可以区间内进行矩阵快速幂；区间大小  i -->p/(p/i);

 

 

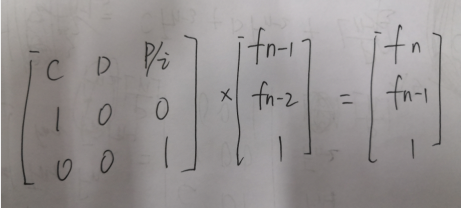
 1 #include<bits/stdc++.h>
 2 #define ll long long
 3 using namespace std;
 4 const ll MOD=1e9+7;
 5 const int maxn=1e5+5;
 6 
 7 struct mat
 8 {
 9     ll a[3][3];
10     mat(){
11         memset(a,0,sizeof(a));
12     }
13     mat operator * (const mat &x)const
14     {
15         mat res;
16         for(int i=0;i<3;i++){
17             for(int j=0;j<3;j++){
18                 for(int k=0;k<3;k++){
19                     res.a[i][j]=(res.a[i][j]+a[i][k]*x.a[k][j]%MOD)%MOD;
20                 }
21            }
22        }
23        return res;
24     }
25 };
26 mat qpow(mat x,ll p)
27 {
28     mat res;
29     res.a[0][0]=res.a[1][1]=res.a[2][2]=1;
30     while(p)
31     {
32         if(p&1){
33             res=res*x;
34         }
35         x=x*x;
36         p>>=1;
37     }
38     return res;
39 }
40 int main()
41 {
42     int t;
43     scanf("%d",&t);
44     while(t--)
45     {
46         ll A,b,c,d,p,n;
47         scanf("%lld%lld%lld%lld%lld%lld",&A,&b,&c,&d,&p,&n);
48         if(n==1){
49             printf("%lld\n",A);
50         }
51         else if(n==2){
52             printf("%lld\n",b);
53         }
54         else{
55             mat ans,ant,bb;
56             ans.a[0][0]=d;ans.a[0][1]=c;
57             ans.a[1][0]=ans.a[2][2]=1;
58             ans.a[1][1]=ans.a[1][2]=ans.a[2][0]=ans.a[2][1]=0;
59 
60             ant.a[0][0]=b;ant.a[1][0]=A;ant.a[2][0]=1;
61 
62             for(ll i=3,j;i<=n;i=j+1)
63             {
64                 ans.a[0][2]=p/i;
65                 if(p/i==0){
66                     bb=qpow(ans,n-i+1);
67                     ant=bb*ant;
68                     break;
69                 }
70                 j=min(p/(p/i),n);
71                 bb=qpow(ans,j-i+1);
72                 ant=bb*ant;
73             }
74             printf("%lld\n",ant.a[0][0]%MOD);
75         }
76     }
77     return 0;
78 }
View Code

 

2019-10-30

posted @ 2019-10-30 20:44  sj-_-js  阅读(240)  评论(0)  编辑  收藏  举报