Luogu P7503 「HMOI R1」文化课
先想一个巨 shaber 的暴力 DP:设 为对前 个人分段的最优解,则:
其中:
暴力做显然是 的,考虑优化。
如果考虑将决策中的 右移一位,用线段树维护 的话,发现右移时无法快速修改有变化的位置(类似 状物,不好维护)。
正难则反,考虑某个 会对哪些决策位置 有贡献。
我们将判断条件 拆成两部分: 和 。
不难画出下图:
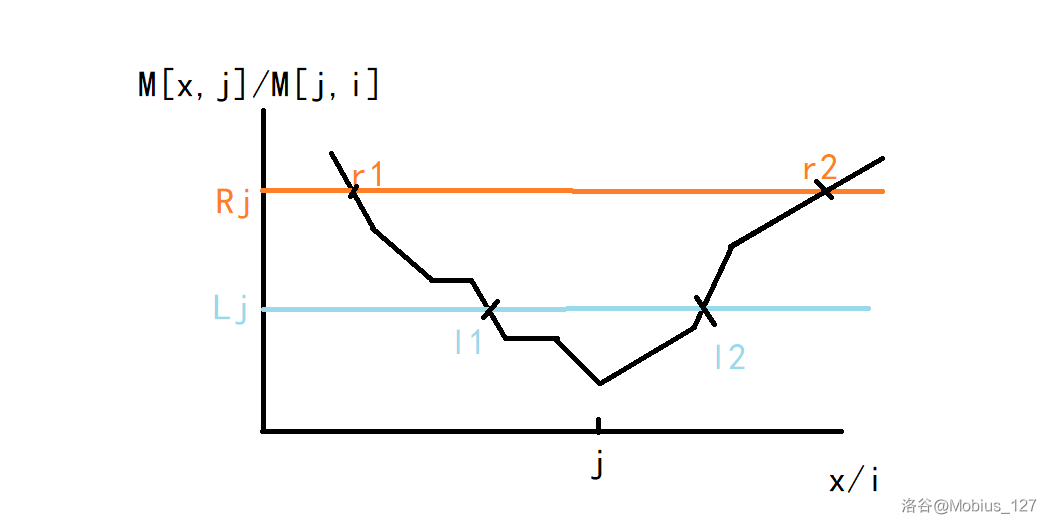
先考虑 ,对于这一段位置, 已经满足了 ,那么 只要在 之间即可。
然后是 ,此时 就必须满足 ,即 。
对于 ,显然 已经贡献不到了。
然后你就发现每个 贡献到的 是连续的,而且对于每个被贡献到的 ,函数 区间左端点 也是连续的。
所以我们在 处塞一个 区间 +1 的操作,在 处塞一个 区间 +1 的操作( 在前面已经被加过一次了)。
然后在 的位置塞一个消除贡献的区间 -1 操作即可。
操作数显然是 的, 可以单调栈后二分找。
总复杂度 。
Code
#include <stdio.h>
#include <algorithm>
#include <string.h>
#include <cctype>
#include <vector>
#define st first
#define nd second
using namespace std;
typedef long long ll;
typedef pair <int, int> Pii;
const int INF=0x3f3f3f3f;
const int mo=1e9+7;
inline int read(){
char ch=getchar();int x=0, f=1;
while(!isdigit(ch)){if(ch=='-') f=-1; ch=getchar();}
while(isdigit(ch)){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();}
return x*f;
}
inline void write(int x){
if(x<0) putchar('-'), x=-x;
if(x>9) write(x/10);
putchar(x%10+'0');
}
inline int ksm(int a, int b){
int ret=1;
for(; b; b>>=1, a=1ll*a*a%mo)
if(b&1) ret=1ll*ret*a%mo;
return ret;
}
const int N=1e5+5;
namespace Segment{
#define ls k<<1
#define rs k<<1|1
#define mid (l+r>>1)
int Mx[N*4], tag[N*4];
void build(){
memset(Mx, -9, sizeof(Mx));
memset(tag, 0, sizeof(tag));
}
void upd(int k, int v){Mx[k]+=v, tag[k]+=v;}
void pushdown(int k){if(tag[k]) upd(ls, tag[k]), upd(rs, tag[k]), tag[k]=0;}
void pushup(int k){Mx[k]=max(Mx[ls], Mx[rs]);}
void change(int k, int l, int r, int x, int v){
if(l==r) return (void)(Mx[k]=max(Mx[k], v));pushdown(k);
if(x<=mid) change(ls, l, mid, x, v);
else change(rs, mid+1, r, x, v);
pushup(k);
}
void modify(int k, int l, int r, int x, int y, int v){
if(x>y) return ;//if(k==1) printf("make %d %d %d\n", x, y, v);
if(x<=l&&r<=y) return upd(k, v);pushdown(k);
if(x<=mid) modify(ls, l, mid, x, y, v);
if(mid<y) modify(rs, mid+1, r, x, y, v);
pushup(k);
}
#undef ls
#undef rs
#undef mid
}
int n, a[N], la[N], ra[N], f[N];
Pii L[N], R[N];
vector < pair<Pii, int> > op[N];
int sta[N], top=0;
int find(int x){
int l=1, r=top, ans=0;
while(l<=r){
int mid=l+r>>1;
if(a[sta[mid]]>=x) l=mid+1, ans=mid;
else r=mid-1;
}
return sta[ans];
}
signed main(){
n=read();
for(int i=1; i<=n; ++i) a[i]=read();
for(int i=1; i<=n; ++i) la[i]=read(), ra[i]=read();
top=0;
for(int i=1; i<=n; ++i){
while(top&&a[sta[top]]<a[i]) --top;
sta[++top]=i;L[i]=make_pair(find(la[i]), find(ra[i]+1)+1);
}
sta[top=0]=n+1;
for(int i=n; i>=1; --i){
while(top&&a[sta[top]]<a[i]) --top;
sta[++top]=i;R[i]=make_pair(find(la[i]), find(ra[i]+1));
// printf("(%d %d)\n", R[i].first, R[i].second-1);
}
for(int i=1; i<=n; ++i)
if(a[i]<=ra[i])
op[i].push_back(make_pair((Pii){L[i].nd, L[i].st}, 1)),
op[R[i].st].push_back(make_pair((Pii){L[i].st+1, i}, 1)),
op[R[i].nd].push_back(make_pair((Pii){L[i].nd, i}, -1));
int ans=0;Segment :: build();
for(int i=1; i<=n; ++i){
// printf("for %d\n", i);
Segment :: change(1, 1, n, i, f[i-1]);
for(auto x : op[i])
Segment :: modify(1, 1, n, x.st.st, x.st.nd, x.nd);
f[i]=Segment :: Mx[1];
// printf("find %d\n", f[i]);
ans=max(f[i], ans);
}
printf("%d\n", ans);
return 0;
}
本文作者:127_127_127
本文链接:https://www.cnblogs.com/sizeof127/p/16748074.html
版权声明:本作品采用知识共享署名-非商业性使用-禁止演绎 2.5 中国大陆许可协议进行许可。




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步