初赛零散知识点
Linux 命令
directory 意为“目录”。
mkdir：即 make directory，新建文件（目录）
cp：即 copy，复制文件（目录）
mv：即 move，移动文件（目录）
rm：即 remove，删除文件（目录）
cd：即 change directory，更改文件（目录）
pwd：即 print working directory，输出（显示）当前所在文件（目录）
ls：即 list，查看文件（目录）
数码转换
D/B/O/H 分别是 十进制/二进制/八进制/十六进制。
即 \((255)_D=(11111111)_B=(377)_O\)。
base64：先 A-Z，再a-z，最后是 0-9 以及 + 和 /。
ASCII 码：0 48，A 65，a 97，<=> 为 60/61/62，+-*/ 分别为 43/45/42/47。
区位码、国标码：表示汉字，\((\text{区位码})_{H}+(2020)_H=(\text{国标码})_{H}\)
原码：有符号二进制数，负数的最高为为 1，正数为 0
反码：正数不变，负数除符号位取反。
补码：反码 + [是否为负数]
负数以补码形式参与位运算！
运算符优先级：
第一级：后缀，即 () [] -> . 和自加减 ++ --
第二级：一元运算符，正负号（不是加减）+ -，逻辑非 !，按位取反 ~，取地址符号 &
第三级：四则运算 */% > +-
第四级：移位（左移右移）
第五级：大小关系符号 < <= > >= == !=
第六级：二元位运算 & > ^ > |
第七级：逻辑二元运算符 && > ||
第八级：三目运算符
第九级：赋值 = += -= *= &= |= ...
第十级：逗号 ,
奇怪的东西
TCP-IP 协议分别为 传输层 和 网络层协议
C 语言是面向过程编程语言。
面向对象编程语言有 C++、Jvav、C#、PHP、python、visual basic（VB）
文件大小
老生常谈
分辨率=位深/8
排序
以下用 \(O(f(n))-O(g(n))\) 来表示最优/最劣复杂度。
偷个图
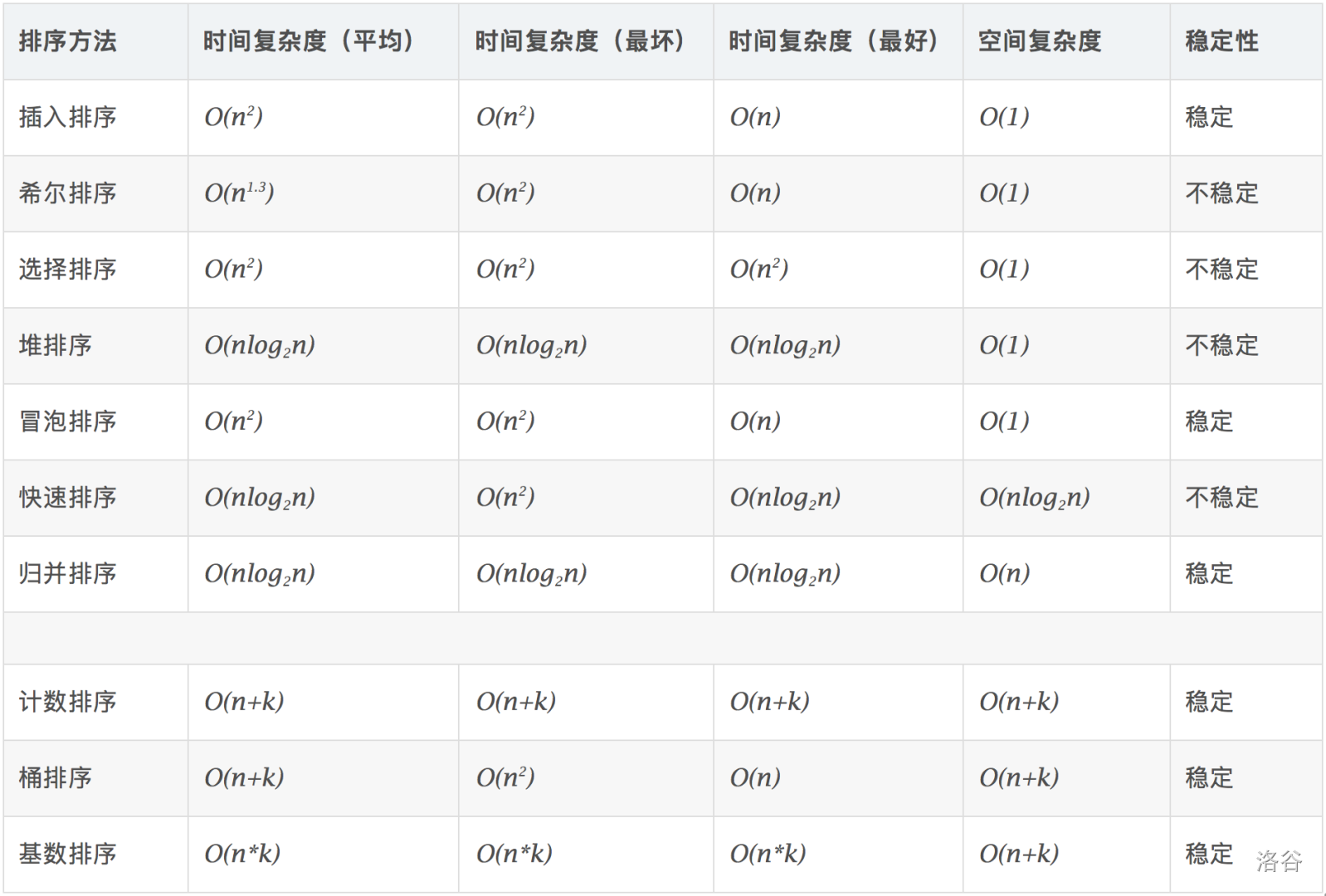
插入排序
遍历 \(i:[1, n]\) 将 \(a_i\) 与 \(j:(i, 1]\)（倒序）比较，若 \(a_i < a_j\) 则交换并 \(j--\)，否则停止。
数组顺序时不会交换，倒序时会被卡满，因此复杂度为 \(O(n)-O(n^2)\)，由于交换的两个位置严格小于，所以是稳定的。
希尔排序
每次选择一个增量 \(d\)，将下标序列分别为等差数列 \([kd],[kd+1],\dots [kd+k-1]\) 中的元素分为 \(k\) 组，每组内部使用插入排序，期望复杂度比插入排序略优为 \(O(n^{1.3-2})\)，但照样能卡满。
但是由于对下标进行了分组，导致某个 \(a_i=a_j, i<j\) 的 \(j\) 可能会被换到 \(i\) 前面（此时 \(i, j\) 不同组）。
选择排序
遍历 \(i:[1, n]\)，从 \([i, n]\) 中找到最小值 \(a_j\)，执行 \(\operatorname{swap}(a_i, a_j)\)，复杂度显然是 \(O(n^2)\) 的。
为什么不稳定呢？因为我们把原来的 \(a_i\) 换到后面去了，如 \(a=[2, 2, 1]\)，第一个二就被我们丢到了后面。
堆排序
应该不会有人不知道吧？
冒泡排序
不会有人不会吧？
稳定性：由于我们是 \(i:[1, n], then\ j:[i, n]\) 并且是判 \(<\)，不会破坏稳定性。
快速排序
sort
分治 \([l, r]\)，选择一个基准 \(mid\)，将 \(< a_mid\) 的放 mid 前面，否则放后面，随后分治 sort 被 mid 切开的两个区间（不包含 mid）。
由于我们把 \(\ge a_mid\) 的全丢到 mid 后面了，这样就破坏了稳定性。
