[字符串] 基本子串结构
提示
这个博客是差不多就是学习笔记,因此有些重要的但是比较显然的定义/定理被省略掉了,并且有些符号用得很奇怪,建议看看参考资料。
原论文的定义/定理/推论的标记号我看不懂关联,于是按照自己的方式编了个号(引理/推论的第一个数字表示与哪个定义相关,推论第二个数字表示与哪个引理相关)。
符号约定
两个串 \(A, B\),若 \(A\subseteq B\),则表示 \(A\) 是 \(B\) 的子串。
注意区分本文中 等价类,行等价类(endpos 等价类),列等价类(startpos 等价类)的区别。以及 SAM(SAM 的 DAWG)和 SAM 的 parent 树的区别。
拓展串
定义 0(出现次数)
定义 \(s\) 的 一个子串 \(t\) 在 \(s\) 的出现次数为 \(\operatorname{occ}(t)\)。
定理 0
若 \(t\subseteq T\),那么 \(\operatorname{occ}(T)\le\operatorname{occ}(t)\)
证明:若 \(T\) 出现一次则 \(t\) 必然会出现一次。
定义 1(拓展串)
定义 \(t\) 的拓展串 \(\operatorname{ext}(t)=T \to (\max_{t\subseteq T, \operatorname{occ}(T)=\operatorname{occ}(t)} |T|)\)。
定理 1.1
\(\operatorname{ext}(t)\) 存在且唯一。
证明:\(t\) 自身即为 \(\operatorname{ext}(t)\) 一个合法的选项,这是存在性;若两个不同串 \(T1, T2\) 均为为 \(\operatorname{ext}(t)\),那么 \(T1\cup T2\) 是一个更大且合法的串,矛盾,唯一性得证。
不难进一步得出:
推论 1.1.1
若 \(t\subseteq p \subseteq T\),且 \(\operatorname{ext}(t)=T\),那么 \(\operatorname{ext}(q)=T\)。
等价类
定义 2(等价类)
对于两个子串 \(x, y\),若 \(\operatorname{ext}(x)=\operatorname{ext}(y)\),则我们说 \(x, y\) 是一个等价类。
对比 SAM,我们发现这里的“等价类”其实是一些等效位置的子串,而 SAM 的 endpos 等价类是一些等效结束位置的子串,相当于 \(\operatorname{ext}(t)\) 只向左拓展。
定义 3(代表元)
若 \(\operatorname{ext}(t)=t\),则称 \(t\) 是其所在的等价类 \(a\) 的代表元 \(\operatorname{rep}(a)\)。
不难发现 \(\operatorname{rep}(a)\) 存在且唯一。
定理 0/2.1
若 \(t_{1}\subseteq t_{2}\),且 \(\operatorname{occ}(t_{1})=\operatorname{occ}(t_{2})\),那么 \(t_{1},t_{2}\) 属于同一个等价类。
定理 2.2
如果 \(s[l, r_1]\) 与 \(s[l, r_2]\) 在同一个等价类中,那么对 \(\forall 1 \le i < l\),\(s[i, r_1]\) 与 \(s[i, r_2]\) 在同一个等价类中。
如果 \(s[l_1, r]\) 与 \(s[l_2, r]\) 在同一个等价类中,那么对 \(\forall r< i\le |s|\),\(s[l_1, i]\) 与 \(s[l_2, i]\) 在同一个等价类中。
证明:不妨设 \(r_1<r_2\),因为 \(s_{[l, r_{1}]}\subseteq s_{[i, r_1]}\),\(s_{[i, r_1]}\) 的一次出现意味着 \(s_{[l, r_{1}]}\) 作为其后缀出现,同时因为 \(s_{[l, r_{1}]}, s_{[l, r_{2}]}\) 属于同一等价类,所以 \(s_{[i, r_1]}\) 后还跟着 \(s_{(r_{1}, s_{r_{2}}]}\),即 \(s_{[i, r_2]}\) 也出现了。即 \(s_{[i, r_1]},s_{[i, r_2]}\) 一一对应,在一个等价类中。第二条同理
阶梯状图形
定义 4(首次出现位置 first occurence)
对于子串 \(t\),定义 \(\operatorname{posl}(t), \operatorname{posr}(t)\) 为最小的一对数使得 \(s_{[\operatorname{posl}(t), \operatorname{posr}(t)]}=t\)。
以 \(s=\texttt{aababcd}\) 为例,我们建立如下一个格点图:横轴为 \(l\),竖轴为 \(r\),一个点 \([l, r]\) 为 \(s_{[l, r]}\)(\(y=x\) 下面为空)。
我们先将等价类列出来:
在格点图上标记。
定义 4.1(格点图)
名字是瞎起的哦平面直角坐标系上一点 \((l, r)\) 表示子串 \(s_{[l, r]}\)。\(\frac{n(n+1)}{2}\) 个子串形成格点图。
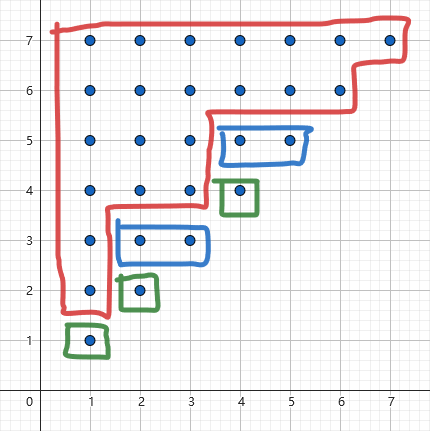
定理 2/5.1
等价类形成了若干个上侧与左侧对齐,右侧与下侧呈阶梯状上升的点阵。
证明:取一等价类 \(a\),不妨设 \([\operatorname{posl}(\operatorname{rep}(a)), \operatorname{posr}(\operatorname{rep}(a))]=[l_{0}, r_{0}]\),对于等价类的另一个非代表元的子串 \(s_{[x, y]}\),由 定理 2.2 得 \(\forall l_{0}\le a\le x \le y \le b\le r_{0}\),\(s_{[a, b]}\) 仍在这个等价类中,即 \([a, b]\) 在这个等价类点阵中,那么一个等价类其实就是若干个左上角为 \([l_{0}, r_{0}]\) 的矩形的并,即阶梯状点阵。
定义 5(点阵)
设 \(\operatorname{G}(a)\) 为 \(a\) 代表的一个阶梯点阵,记 \(\operatorname{rowsize}(a), \operatorname{colsize}(a)\) 分别为 \(G(a)\) 的行数和列数。
论文中没有明确一个符号来表示它,但是用符号确实能少打几个字。
推论 5.1
某个 \(\operatorname{G}(a)\) 会出现 \(\operatorname{occ}(\operatorname{rep}(a))\) 次。
定义 6(周长)
定义等价类 \(a\) 的周长 \(\operatorname{per}(a)=\operatorname{rowsize}(a)+\operatorname{colsize}(a)\),即 \(\operatorname{G}(a)\) 的行数和列数和。
定理 2/5.2(重要)
对于一个等价类 \(a\),\(\operatorname{G}(a)\) 的每一行对应了一个 endpos 等价类,每一列对应了一个 startpos 等价类。换言之,每一行对应了正串 SAM parent 树上的一个结点,每一列对应了反串 SAM parent 树上的一个结点。
证明:以行为例,设这一行纵坐标为 \(r\),由于该行表示的字符串互为后缀,且 \(\operatorname{occ}\) 相等,所以它们必然在一个 endpos 等价类 \(U\) 里,假设 \(U\) 内若干个串不在 \(a\) 中,由 endpos 等价类的连续性得出必然有个某个不合法串为 \(t=s_{[\operatorname{posl}(\operatorname{rep}(a))-1, r]}\),又 \(\operatorname{occ}(t)=\operatorname{occ}(\operatorname{rep}(a))=\operatorname{occ}(\text{行内某个串} q)\),由 \(\operatorname{ext}(q)\) 的唯一性(引理 1.1)得知其矛盾。因此得到对应关系。
由次不难导出:
定理 5/6.1
\(\sum\operatorname{per}(a)=O(n)\),即正反串 SAM 的结点个数和。
构建
定义 7(基本子串结构)
基本子串的定义十分笼统,不过你可以看成它是正反串 SAM 的结合体,即对于所有本质不同子串状态之间的自动机。
对于一个子串 \(s_{[l, r]}\) 在前/后面接一个字符 \(c\) 进行匹配,这对应在格点图上其实就是“向左走”(\(l-1\))和“向上走”(\(r+1\)),因此,基本子串结构中的字符边可以看为某个点对四联通结点的连边。但边的数量实在太大,于是就有了等价类,等价类中的某行和相邻行的连边,此时边上的字符变成了一个可长可短的字符串(视改行某个点而定)。
考虑先找出一个等价类的标识——代表元,由定理 2/5.2可得 \(\operatorname{rep}(a)\) 在所在的行 endpos 等价类的最左侧、列 startpos 等价类最上侧,都是它们中的最长串,而对于 \(a\) 中的非代表元串,其总是不能同时满足这两个条件。换言之,所有满足 \(r-l+1=len_{\text{正} \operatorname{SAM}}=len_{\text{反} \operatorname{SAM}}\) 的子串 \(s_{[l, r]}\) 与等价类的代表元一一对应。这些代表元可以通过枚举正串 SAM 的结点,在反串 SAM 上倍增查询,做到 \(O(n\log n)\) 复杂度。
接下来考虑不包含代表元的 endpos 等价类和 startpos 等价类,一个非常笨比的做法是按 \(\operatorname{occ}\) 扫描线后找最小包含区间,但是这样码量过于抽象,所以想想一个稍微要点脑子的做法,这里给出一个引理。
定理 2/5.3
对于一个 endpos 等价类 \(X\),若它不是所属等价类 \(\operatorname{G}(a)\) 中的上边界,那么其在正 SAM 上有且只有一条出边,且该出边指向其在 \(\operatorname{G}(a)\) 的上一行。startpos 等价类同理。
其实这个定理还有另外一部分,但是我看不懂,看懂的老哥给我讲讲。
证明:我们之前说过,“向上走”意味着向后接一个字符,这在 SAM 上就是一条转移边,而如果一个 endpos 等价类 \(p\) 向后只有一条转移边 \((p, q, ch)\)。则说明 \(\operatorname{occ}(p)=\operatorname{occ}(q)\),由推论 1.1.1可得 \(p,q\) 属于同一个等价类。而这个关系是双向的(一一对应)。
于是可以按 DAG 的拓扑序来合并,其实也就是按 \(len\) 从大到小来合并。
而论文指出,按 SAM 结点顺序倒序合并也是可以的:
将两个 SAM 的等价类对应起来只需分别找到代表元的 posl, posr 即可。每块中网格图
的构建只需将所有 SAM 节点按照 r 或 l 进行排序,但其天然与 SAM 构建时加入的顺序相
同。至此所有信息都已构建完毕,总时间复杂度为 O(n)。
我们考虑在同一个等价类 \(a\) 中的所有 endpos 等价类,根据 定理 2/5.3,这些 endpos 等价类在 SAM 中成一条除首尾外没有其它出边的链,它们各自的最长串其实就是 \(G(a)\) 中最左侧的一列点,在这一列 \(l\) 不变 \(r\) 递增,联系的 SAM 的构建过程,我们发现越靠上的 endpos 等价类越晚形成(因为 \(r\) 更大),也就是说编号也更大,所以我们直接倒序遍历所有点进行合并即可,
于是合并时间就莫名奇妙地变成 \(O(n)\) 的了。
参考代码
#define vi vector
const int N=1e5+5;
const int M=N<<1;
int n, Ec;char s[N];
struct SAM{
int ndc, lst, pos[N], mnpos[M], siz[M], id[M];
struct node{int fa, len, son[26];}sam[M];
int clr(int x){sam[x]=sam[0];return x;}
void init(){clr(ndc=lst=1);}
int insert(char cr){
int c=cr-'a';int cur=clr(++ndc), p=lst;
sam[cur].len=sam[lst].len+1;
for(; p&&!sam[p].son[c]; p=sam[p].fa) sam[p].son[c]=cur;
int q=sam[p].son[c];
if(!q) sam[cur].fa=1;
else if(sam[q].len==sam[p].len+1) sam[cur].fa=q;
else{
int nxt=clr(++ndc);sam[nxt]=sam[q], sam[nxt].len=sam[p].len+1;
for(; p&&sam[p].son[c]==q; p=sam[p].fa) sam[p].son[c]=nxt;
sam[cur].fa=sam[q].fa=nxt;
}
return lst=cur;
}
vi G[M];int fa[M][20];
void chk(int &x, int v){if(!x) x=v;else if(v) x=min(x, v);}
void dfs(int x){
for(int i=1; i<20; ++i) fa[x][i]=fa[fa[x][i-1]][i-1];
for(auto v:G[x]) fa[v][0]=x, dfs(v), chk(mnpos[x], mnpos[v]);
}
int FindR(int l, int r){
int x=pos[r];
for(int i=19; i>=0; --i) if(sam[fa[x][i]].len>=r-l+1) x=fa[x][i];
return x;
}
void ins(char *t, int m){
init();
for(int i=1; i<=m; ++i) mnpos[pos[i]=insert(t[i])]=i;
for(int i=2; i<=ndc; ++i)
G[sam[i].fa].pb(i), siz[i]=sam[i].len-sam[sam[i].fa].len;
dfs(1);
}
void merge(){
for(int i=ndc; i>1; --i) if(!id[i])
for(int c=0; c<26; ++c) if(sam[i].son[c])
{id[i]=id[sam[i].son[c]];break;}
}
}S, T;
vi row[M], col[M];
void build(){
S.ins(s, n);reverse(s+1, s+n+1);T.ins(s, n);
for(int i=2; i<=S.ndc; ++i){
int r=S.mnpos[i], l=r-S.sam[i].len+1, u=T.FindR(n-r+1, n-l+1);
if(r-l+1==T.sam[u].len) S.id[i]=T.id[u]=++Ec;
}
S.merge();T.merge();
for(int i=S.ndc; i>=2; --i) row[S.id[i]].pb(i);
for(int i=T.ndc; i>=2; --i) col[T.id[i]].pb(i);
}
其中 \(\operatorname{row}, \operatorname{col}\) 分别存储了第 \(i\) 个等价类包含的 endpos/startpos 等价类在正/反串 SAM 的编号。
为什么要这里也要从末尾开始?因为这样加入使得 \(\operatorname{row},\operatorname{col}\) 中的 endpos/startpos 等价类都按照了自身集合大小加入(从大到小),也就是说 \(\operatorname{row}_{a}[0]=\operatorname{col}_{a}[0]=\operatorname{rep}(a)\)。
SAM 之死
这里先给出另一个引理:
定理 2/5.4
对于一个等价类 \(a\),其包含的某个行等价类(endpos 等价类),经过上移若干单位后,仍被某一等价类 \(b\) 完全包含。
而对于某个列等价类(startpos 等价类),经过左移若干单位后,仍被某一等价类 \(b\) 完全包含。
其实本质上就是 定理 2.2
这个定理说明了在等价类阶梯点图中,等价类向上/左只会碰到一个等价类。
考虑串 \(s=\operatorname{ababababba}\):
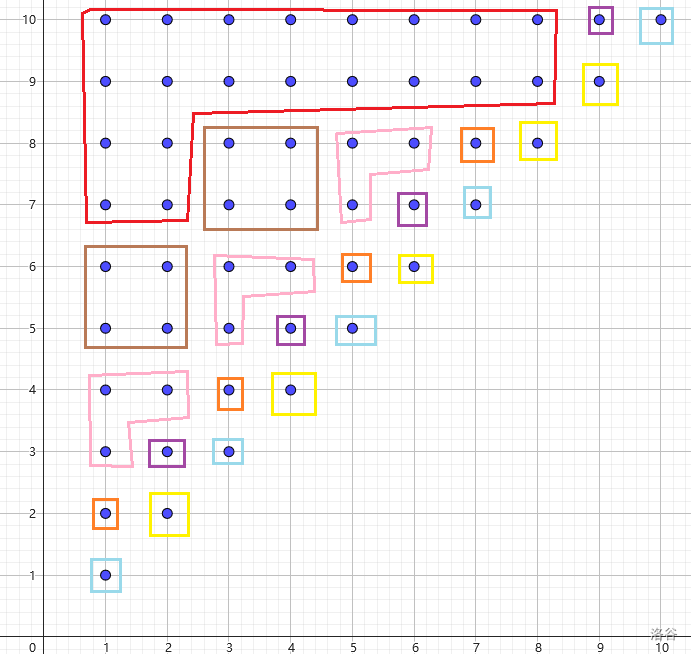
考虑等价类 \(a=\{\texttt{aba}, \texttt{bab}, \texttt{abab}\}\)(粉色的阶梯状点阵),让它在 \(r=4\) 的位置 “向上走”,走完了另一等价类,\(\{\texttt{aba},\texttt{abab}\}_{13}\to \{\texttt{ababa}, \texttt{ababab}\}_{17}+\{\texttt{ababb}, \texttt{ababba}\}_{8}\),\(\texttt{bab}_{11}\to\{\texttt{baba}, \texttt{babab}\}_{15}+\{\texttt{babb}, \texttt{babba}\}_{7}\)(右下角的数字表示它们在反串 SAM 上对应的结点),注意到它们向上走分别对应了一个完整的 startpos 等价类,我们考虑将 \(a\) 也划分为 startpos 等价类,不难发现这种“向上走”的转移恰好就是反 SAM parent 树上的边。
从这里,我们可以导出定理 2/5.3的下半部分。没错我最后看懂了
定理 2/5.3(完整)
对于一个 endpos 等价类 \(X\),若它不是所属等价类 \(\operatorname{G}(a)\) 中的上边界,那么其在正 SAM 上有且只有一条出边,且该出边指向其在 \(\operatorname{G}(a)\) 的上一行。如果其对应的是上边界,则它的所有出边即连向((从该上边界用另一棵 SAM 的 parent 树边连出能到的所有下边界)表示的 SAM 节点)。startpos 等价类同理。
而在定义 7,我们说明了“向上走”同时也相当于在后面接上一个字符,一个在等价类 \(a\) 最上面部分的 endpos 等价类 \(q\),它在正 SAM DAWG 上的转移边等效于某条反 SAM parent 树上的边,而这些边又相当于不同等价类之间列 startpos 等价类的转移!于是,我们用阶梯状点图和等价类划分完美描述了两个 SAM 的结构!
定理 2/5.5(重要)
正 SAM parent 树上的边与列等价类之间的转移有对应关系,正 SAM DAWG 的转移边与行等价类的转移有对应关系;
反 SAM parent 树上的边与行等价类之间的转移有对应关系,反 SAM DAWG 的转移边与列等价类的转移有对应关系。
这个定理是我瞎捏的,跟论文无关,其实本质上就是 定理 2/5.3 的笼统描述。
SAM 已死,基本子串当立!
线性构造
回头看看我们 \(O(n\log n)\) 建立基本子串的过程,发现瓶颈在于如何快速地处理代表元。
首先根据定理 2/5.5,不难发现代表元所在的等价类的最上面/左边的行/列等价类在 SAM 的 DAWG 上,要么没有出边,要么出边连向的 endpos/startpos 等价类与自己的 \(\operatorname{occ}\) 不同(这种关系是一一对应的,即不存在一个满足条件的 endpos/startpos 等价类,它的最长串不是代表元),于是可以很简单的找到代表元的个数。
参考代码
int repcnt=0;
for(int i=ndc; i>1; --i){
bool flg=0;int p=0;
for(int c=0; c<26; ++c)
if(sam[i].son[c]){
++p;
if(cnt[sam[i].son[c]]!=cnt[i]){flg=1;break;}
}
if(flg||p==0) ++repcnt;
}
但是这样是远远不行的,我们真正要做的事是将正反串的代表元对应起来。
将 \(O(n\log n)\) 找代表元做法还原,我们枚举每一个 endpos 等价类中的最长串,直接在反串 SAM 的 DAWG 上去匹配到对应节点。
这样做显然是 \(O(n^2)\) 级别的复杂度,能不能做到类似于双指针一样的操作呢?
这里给出一个性质:在 SAM 的 DAWG 上,如果我们只走 \(len_{x}+1=len_{sam_{x, c}}\) 的点,是能够走完全部节点的。(证明很简单,除根节点外每个点都必然找得到这么一条连向自己的边,于是形成了一棵树)。
为什么要这么走呢?
-
若 \(x\) 与 \(son_{x, c}\) 属于同一个等价类,那么根据 定理 2/5.3,\(x\) 只有一条出边 \((x, son_{x, c}, c)\),且 \(x\) 代表的 endpos 等价类与 \(son_{x, c}\) 代表的 endpos 等价类在阶梯状点图中是相邻两行的关系,由于 \(len\) 是 endpos 等价类中最长的串,即只跟行等价类的左端点有关,而我们知道等价类的点图左侧对齐,因此两个 endpos 等价类最长串 \(l\) 相同,\(r\) 相差 1,因此就有 \(len_{x}+1=len_{sam_{x, c}}\)。
-
若 \(x\) 与 \(son_{x, c}\) 属于不同等价类,根据 定理 2.2 这时候我们所有的出边都指向了同一个等价类,只能走最短的行等价类,于是就走 \(len_{x}+1=len_{sam_{x, c}}\) 的边即可。
接下来我们考虑如何在反串 SAM 上执行这个“向前面加字符”的匹配过程。
向前加单个字符,满足原串是新串的一个后缀,因此它们在 parent 树上必然是父子,我们考虑预处理时用儿子去更新父亲的匹配边:设某个出现的位置末是 \(pos\)(实际上应该是开始的位置,但是由于是反串的 SAM,于是变成了末位置),父亲最大串长为 \(len\),那么父亲到儿子的匹配边字符即为 \(s_{pos-len}\)。
参考代码
for(int i=2; i<=ndc; ++i)
son[sam[i].fa][s[pos[i]-sam[sam[i].fa].len]-'a']=i;
但是,注意我们实际上维护的是最长串的位置,在同等价类中行等价类的链上转移中,我们维护的最长串一直在最左边的列等价类(一直在左边界向上走),因此,只有在 DAWG 的转移边中,两端不属于同一等价类时才要用 son 转移,此时必然满足起点是代表元之一,可以参考代码理解。
参考代码
const int M=N<<1;
int n, Ec;char s[N];
struct SAM{
int ndc, lst, pos[N], mnpos[M], siz[M], id[M], cnt[M], fail[M][26];
struct node{int fa, len, son[26];}sam[M];
int clr(int x){sam[x]=sam[0];return x;}
void init(){clr(ndc=lst=1);}
int insert(char cr){
int c=cr-'a';int cur=clr(++ndc), p=lst;
sam[cur].len=sam[lst].len+1;
for(; p&&!sam[p].son[c]; p=sam[p].fa) sam[p].son[c]=cur;
int q=sam[p].son[c];
if(!q) sam[cur].fa=1;
else if(sam[q].len==sam[p].len+1) sam[cur].fa=q;
else{
int nxt=clr(++ndc);sam[nxt]=sam[q], sam[nxt].len=sam[p].len+1;
for(; p&&sam[p].son[c]==q; p=sam[p].fa) sam[p].son[c]=nxt;
sam[cur].fa=sam[q].fa=nxt;
}
return lst=cur;
}
vi G[M];
void chk(int &x, int v){if(!x) x=v;else if(v) x=min(x, v);}
void dfs(int x){for(auto v:G[x]) dfs(v), chk(mnpos[x], mnpos[v]), cnt[x]+=cnt[v];}
void ins(char *t, int m){
init();
for(int i=1; i<=m; ++i) mnpos[pos[i]=insert(t[i])]=i, ++cnt[pos[i]];
for(int i=2; i<=ndc; ++i)
G[sam[i].fa].pb(i), siz[i]=sam[i].len-sam[sam[i].fa].len;
dfs(1);
for(int i=2; i<=ndc; ++i)
fail[sam[i].fa][s[mnpos[i]-sam[sam[i].fa].len]-'a']=i;
}
void merge(){
for(int i=ndc; i>1; --i) if(!id[i])
for(int c=0; c<26; ++c) if(sam[i].son[c])
{id[i]=id[sam[i].son[c]];break;}
}
}S, T;
vi row[M], col[M];
void DFS(int u, int v){
int lenu=S.sam[u].len, lenv=T.sam[v].len;
if(lenu==lenv&&u!=1&&v!=1) S.id[u]=T.id[v]=++Ec;//两边的代表元对应
for(int c=0, x, y; c<26; ++c)
if((x=S.sam[u].son[c])&&(S.sam[x].len==lenu+1)&&(y=(lenu==lenv)?T.fail[v][c]:v))
DFS(x, y);
}
void build(){
S.ins(s, n);reverse(s+1, s+n+1);T.ins(s, n);
DFS(1, 1);//识别代表元
S.merge();T.merge();//合并
for(int i=S.ndc; i>=2; --i) row[S.id[i]].pb(i);
for(int i=T.ndc; i>=2; --i) col[T.id[i]].pb(i);
}
应用
字符串匹配
给定一个串 \(s\) 和另一个空串 \(w\),每次向前/后添加/删除一个字符,若加入字符后 \(w\) 不是 \(s\) 的子串则撤销操作,每次操作后输出是否成功操作,以及当前的 \(\operatorname{occ}(w)\)。
对 \(s\) 建立基本子串结构,这样我们能显式地观察 \(w\) 在阶梯状点阵图的位置,维护 \(w\) 在正反 SAM 上对应的结点,那么每次添加字符无外乎两种可能:在同等价类中走,走出边界。对于第一种情况,我们显然珂以通过简单计算判断应该接上的字符,对于第二种情况,这相当于直接走正/反 SAM 上的字符转移边,同样很容易做到。
CF1817F Entangled Substrings
\(acb\) 打包出现,因此有 \(\operatorname{occ}(a)=\operatorname{occ}(b)\),即 \(a, b\) 属于同一个等价类,因此我们对等价类内部计数。
考虑枚举 \(acb\) 计算合法的 \((a, b)\) 对数,设 \(c\) 在阶梯状点图的坐标为 \((l_{c}, r_{c})\),其向右拓展到 \((l_{p}, r_{c})\),向下拓展到 \((l_{c}, r_{p})\),其中 \(l_{c}\le l_{p},r_{p}\le r_{c}\),又因为点阵的点全在 \(y=x\) 上方,所以右 \(l_{p}\le r_{c}, l_{c}\le r_{p}\)。
可选的 \(a\) 为 \(s_{[l_{c}, [r_{p}, r_{c}]]}\),可选的 \(b\) 为 \(s_{[[l_{c}, l_{p}], r_{c}]}\),并且要满足 \(a\) 的右端点小于 \(b\) 的左端点,即 \(r_{p}\le r_{a}\le r_{c}, l_{c}\le l_{b}\le l_{p}, r_{a}<l_{b}\)。
综合几个不等关系,我们发现 \(r_{p}\le l_{p}\) 才会出现合法的 \((a, b)\),此时 \(a\) 的右端点和 \(b\) 的左端点都落在 \([r_{p}, l_{p}]\) 中,贡献即为 \(C_{l_{p}-r_{p}+1}^{2}\)。
因此我们枚举 \(r_{p}\),双指针维护 \(l_{p}\),统计 \(\sum 1, \sum l, \sum l^2\) 即可。
注意我们在构建基本子串结构时,加入行/列时都是按等价类大小从大到小加入,对应到 \(l_{p}\) 递减,\(r_{p}\) 递增。
注意到我们实际上只需要用到行列等价类的长度,可以通过行的长度来推出列的长度,只建一个 SAM。实现 2
UOJ 577 打击复读
注意到只需要计算 \(wl_{i}\) 的系数就能支持 \(O(1)\) 修改。
注意到 \(vl(s[l, r])\) 和 \(vr(s[l, r])\) 其实就是 \([l, r]\) 在反串/正串 SAM parent 树上对应结点内的所有后缀/前缀的 \(wl_{i}/wr_{i}\) 的和,并且在基本子串结构中,同一列的 \(vl\) 相等,同一行的 \(vr\) 相等。
考虑一个点 \((l, r)\) 的贡献是 \(vl(s[l, r])\times vr(s[l, r])\),于是我们可以通过基本子串结构得到一列 \(vl(s[l, [r1, r2]])\) 的总贡献系数为 \(\sum_{i=r1}^{r2} vr(s[l, i])\times \operatorname{occ}(s[l, r])\),前面的和式本质上是行等价类的一个 \(vr\) 前缀和,再由 \(vl\) 的定义就可以在反串 SAM 的 parent 树上反推 \(wl\) 的系数了,复杂度 \(O(n)\)。代码。
UOJ 697 广为人知题
考虑在格点图上将所有模式串出现的位置的点 +1,于是询问就是求以 \([ql, qr]\) 为左上角的矩形和,直接做是 \(O(n^{2})\) 的。
这样的做法太过冗余了,我们发现答案本质上只跟 \(s_{[ql, qr]}\) 有关,而与 \([ql, qr]\) 无关(即两个询问的答案与位置无关,只跟是否为本质不同子串有关),也由此可以推导出一个结论:
定理 2/5.6
在格点图中, 以 \(\operatorname{rep}(a)\) 出现的所有位置开始,向右、向下完拓展出来的 \(\operatorname{occ}(\operatorname{rep}(a))\) 个大阶梯完全相等。
“相等”指对应位置的每个点属于同一个等价类 \(b\),且在 \(\operatorname{G}(b)\) 的同一个位置。
仍以 \(s=\operatorname{ababababba}\) 为例,其划分等价类后的格点图为:

考虑一个询问 \([1, 5]=[3, 7]\),将其答案统计划为两个部分:\([[1, 2], 5]\) 这条线段以下的部分,以及 \([3, 5]\) 这个子问题询问。
对于前半部分,我们继续将所求划为两个部分:与 \([1, 5]\) 在同一等价类中的点/与 \([1, 5]\) 不在同一等价类中的点。对于同等价类中的点,我们可以直接做一个二维数点,对于非等价类中的点,由于这部分是若干条紧贴着等价类的下边界的竖线段,每条竖线段相当于每个列等价类在反串 SAM 上到根的链的和,所有的和是一个后缀。
对于后半部分,发现我们询问的点在另一个等价类 \(b\) 中最靠左的一个列等价类,考虑先计算出并加上 \(\operatorname{rep}(b)\) 的答案,那么需要减掉的部分的答案是一列的前缀的后缀后的和,这部分是可以简单预处理的。
于是总复杂度 \(O((n+q)\log n)\),代码。
[SDOI/SXOI2022] 子串统计
SDOI 紧跟论文步伐!
列出 \(O(n^{2})\) DP 式子后,在基本子串结构的阶梯点图上优化。详细题解
parent 树的树链剖分
通过前面的理论,我们知道,SAM 的 parent 树上的边本质上是同行不同等价类的行(列)等价类的之间的转移,我们现在通过基本子串结构来反推一些 parent 树的性质。
推论 2.2.1
对于属于同一等价类 \(a\) 两个行(列)等价类 \(u, v\),其所代表的正(反) SAM endpos (startpos)等价类结点在 parent 树上的子树除根节点外同构。
这里同构指可将两棵子树中的点重编号,使得对应结点的出边一致,endpos 等价类的大小一致,且对应节点所在同一个等价类,亦即 \(\operatorname{occ}\) 一致。
证明:我们同时让 \(u, v\) 从最左边同时向左边走(即沿着 parent 树边走),由于定理 2.2,每次走到的两个点 \(p_{u'}, p_{v'}\) 属于同一等价类的两个不同行等价类 \(u', v'\),向左走的时候同时从 \(u', v'\) 的最右侧走到了最左侧,也就是说 \(u', v'\) 的长度(endpos 等价类的大小)相等,考虑每次跨行等价类的时候都是走 parent 树的出边从叶子结点可以归纳证明从 \(u, v\) 的任意的链是完全等价的,再次对 \(u, v\) 的每次出现位置进行合并即可得到子树同构结论。顺带一提,根节点只有 endpos 大小不同。
我们尝试对 SAM 每个结点在阶梯状点图上确定一个位置,使得 SAM 能更好地刻画等价类。
定义 8(结点位置)
令 \(occ=1\) 的行/列等价类的位置就是它唯一出现的位置,接着对于每个重儿子,将其父亲放在其右/下侧,依次类推。
理论上选哪个点进行标记都没有关系,但是考虑到复杂度,优先选择重剖。
仍以 \(s=\operatorname{ababababba}\) 为例:
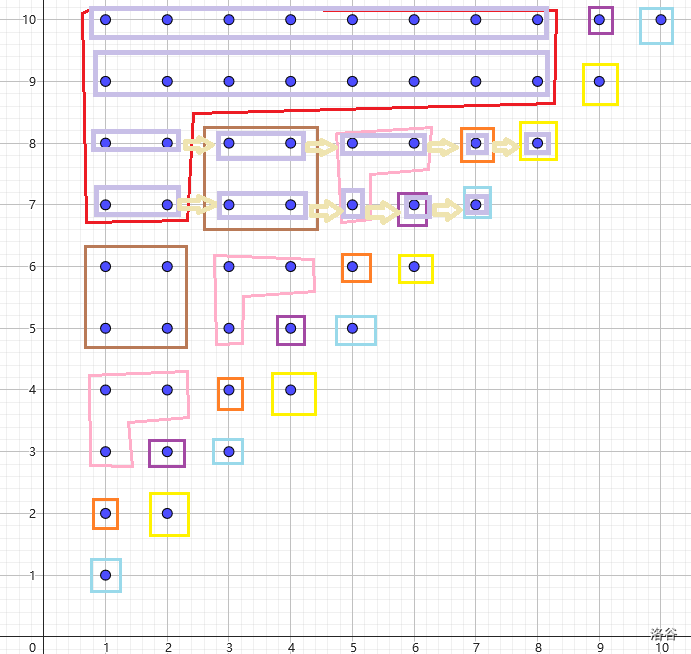
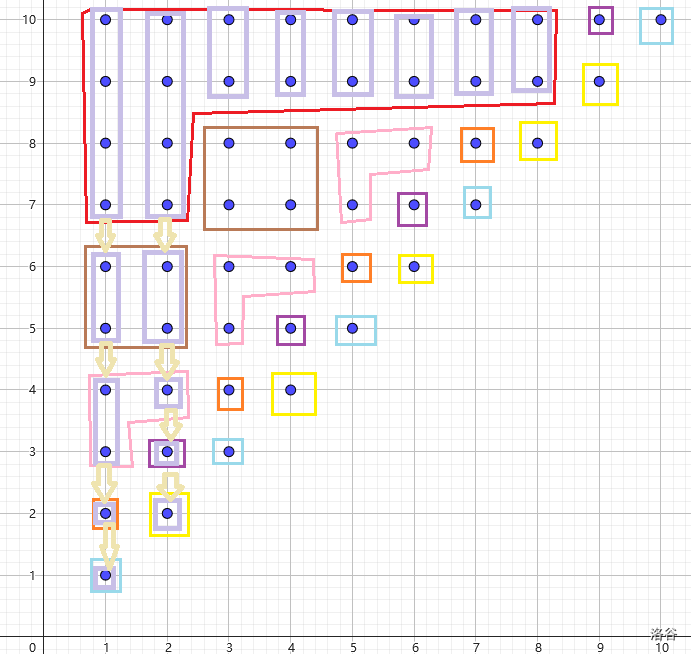
回到 推论 2.2.1,不难得到同等价类中的行等价类在 SAM 上的子树的每个点的重儿子也一一对应。
继续考察。
首先,无论我们链剖以怎样的方式(长剖、短剖、轻剖等),为一条链上的所有点安排的位置的纵坐标 \(r\) 一定相同(或者横坐标 \(l\) 一定相同)。
我们考虑每一个等价类 \(a\) 中的所有行等价类结点,考虑它们所在链的链底,parent 树边只会在 \(l\) 产生改变(换句话说就是一条链的纵坐标不变,因为总有后缀关系),因此这 \(\operatorname{rowsize}(a)\) 条重链的链底的纵坐标连续。
定理 5/8.1
以重链链底所在位置 \([l, r]\) 的 \(r\) 为整条重链标号,则对于任意一个等价类,其行等价类的重链标号为一个连续区间。
同时注意到一条链上的所有本质不同子串(注意这里是子串而并非等价类)的长度互不相同,因此我们可以用 \((\text{反串重链标号},\text{串长})\) 来表示所有的本质不同子串,而根据定理 5/8.1,对于一个行等价类,其包含的所有串的反串重链标号随着串长变大依次 +1 ,即其为一条斜率为 \(1\) 的线段。我们用 \(O(n)\) 的信息量刻画出了所有本质不同子串!
事实上普通的 SAM 也能刻画本质不同子串,在反串 SAM 上,对于一个列等价类,其代表的所有子串是一条竖线段(第一维相同,第二维的区间为 \((fa.len, len]\))。
[BJWC2018] Border 的四种求法
区间最长 border,同时也可以做到数区间 border 个数。
先在正反 SAM 上定位 \(s[l, r]\) 得到两个节点 $u, \(,\)u, v$ 到各自 parent 树根的链分别为 \(s[l, r]\) 后缀和前缀的信息,同时注意 \(u, v\) 所在的等价类会包含一个更大的串,需要加长度 \(\le r-l+1\) 的限制。询问则等价于查询链交。
一个很暴力的做法是,从 \(u\) 开始向上跳,将每个正串 SAM 结点加入到集合中,然后从 \(v\) 开始跳,每次跳到一个点,相当于询问一条横线段与集合中的线段交点信息。
考虑优化:我们发现在 \(v\) 跳的过程中,对于某条重链,其询问的横线段的第一维都是相同的,而第二维都是连续的,这里的连续的意思是,这重链长度个点的横线段可以接在一起,变成一条长线段。右侧的询问个数变为 \(O(\log n)\)。
考虑继续对正 SAM 重剖,这时也出现了 \(O(\log n)\) 条链,然而由于交集的长度限制,正反 SAM 的交叉询问并不是 \(O(\log^2 n)\) 级别,而是 \(O(\log n)\) 条重链对的交。
将这些重链对离线下来,枚举正 SAM 处的重链对处理询问,那么就变成了 \(O(n)\) 次加斜线段,\(O(q\log n)\) 次查询竖线段与斜线段交集信息的问题。总复杂度 \((n+q\log n)\log n\)
更详细的题解和代码见此。
【UNR #6】Border 的第五种求法
你到底有几种求法
同样类似于区间 border,交点的代价变为 \(f_{occ}\),对于正串的一个结点所代表的斜线段上的点,其代价是相同的,同样做二维数点,扫到询问的时候变为求区间和,复杂度不变。代码
Border 的第六种求法
xtq 鸽鸽的论文的最后一题,同 第五种求法,Border \(t\) 的贡献变为 \(f_{\operatorname{occ}}\times g_{|t|}\)。
我们发现做法并不能直接套上去了,这是因为一个 SAM 结点的 \(len\) 并不相同(贡献并不呈线性),我们需要考虑一个更好的做法来统一 \(\operatorname{occ}, len\)。
继续从一个等价类 \(a\) 入手,注意到 \(G(a)\) 中一条斜率为 \(1\) 的线段,它们的 \(len\) 相同,我们考虑对这些斜线计数。
对于这些斜线,它们的 \((\text{正串重链标号}, \text{反串重链标号})\) 跟原下标是一样的一条斜率为 \(1\) 的线段。对于询问,我们发现这两个 重链标号已经被定死了,只剩长度的限制。
具体的,考虑三维坐标 \((\text{正串重链标号}, \text{反串重链标号}, \text{串长})=(x, y, len)\),\(O(n)\) 条 \(len\) 一定,\(y=x+k\) 代价为 \(f_{\operatorname{occ}}g_{len}\) 的线段,\(O(q\log n)\) 次询问 给出一条 \((x, y)\) 一定的线段,查询与 \(O(n)\) 条线段的交集信息。直接对 \((x-y, len)\) 二维数点即可。实现
参考资料
仍然是复读参考资料

