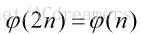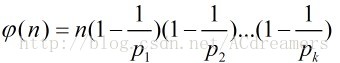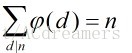欧拉函数知识点及其求法模板

欧拉函数

在数论，对正整数n，欧拉函数是小于n的正整数中与n互质的数的数目（φ(1)=1） 例如φ(8)=4，因为1,3,5,7均和8互质。

欧拉函数有如下基本定理:

一: 是积性函数,设m与n是互素的正整数，那么;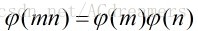

二: ：当n为奇数时，有

三: 设p是素数，a是一个正整数，那么

证明:(

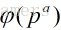
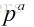
由于表示小于与互素数的正整数个数，所以用减去与它不互素的数的个数就行了。

那么小于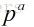与不互素数的个数就是p的倍数个数，有个。所以定理得证。

)

四: 设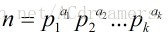为正整数n的素数幂分解，那么

 

五: 设n是一个正整数，那么

 

六: 设n 是一个大于2 的正整数,则 φ(n)是偶数

常用的两个定理:

费马小定理:

当p是质数时   a^(p-1)≡1(mod p)  : 简化幂运算

欧拉定理:

对于和m互素的x，有x^φ(m)≡1(mod m)

直接求法: 适用于求单个 phi值时   此时时间复杂小, 且空间小;

int gphi(int n)
{
    int temp=n;
    for(int i=2;i<=n;i++)
    {
        if(n%i==0)
        {
            temp-=temp/i;
            while(n%i==0)
                n/=i;
        }

    }
    if(n>1)
            temp-=temp/n;
    return temp;
}

模板 求 欧拉函数值;

void get_phi(int n)// p是素数
{
cont=0;
	memset(vis,0,sizeof(vis));
    for(int i=2; i<=n; i++)
	{   
        if(!vis[i])
		{
            p[++cont]=i;
            phi[i] = i-1;   
        }
        for(int j=1; j<=cont && p[j]*i<=n; j++)
		{   
            vis[p[j]*i]=1;
            if(i%p[j]==0)
			{
                phi[i*p[j]] = p[j] * phi[i]; //欧拉函数性质
                break;   
            }
			else phi[i*p[j]] = (p[j]-1) * phi[i];
        }
    }
}

递推法求欧拉函数值:

复杂度 O (nln n)
void iinit()
{
	for(int i=1;i<=N;i++) phi[i]=i;
	for(int i=2;i<=N;i+=2)phi[i]>>=1;
	for(int i=3;i<=N;i+=2){
		if(phi[i]==i)
		{
			for(int j=i;j<=N;j+=i)
				phi[j]=phi[j]-phi[j]/i;
		}
	}
}

看一下应用:

例题一:  POJ 2407 http://poj.org/problem?id=2407

最简单的意思:  求 φ(n)    

直接用第一个:其余的打表模板, 空间占有量太大 n的范围是10^9 次方

#include <iostream>
#include <stdio.h>
#include <algorithm>
#include <cmath>
#include <cstring>

using namespace std;
typedef long long ll;

int gphi(int n)
{
    int temp=n;
    for(int i=2;i<=n;i++)
    {
        if(n%i==0)
        {
            temp-=temp/i;
            while(n%i==0)
                n/=i;
        }

    }
    if(n>1)
            temp-=temp/n;
    return temp;
}
int main()
{
    int n;
    while(cin>>n&&n)
    {
        cout<<gphi(n)<<endl;
    }
    return 0;
}

例题2 :  POJ 1284  http://poj.org/problem?id=1284

原根:  求 x^i mod p = [1,p-1]     p原根的个数;

  这里用到一个结论     如果p 是素数, 则有 φ(p-1)个原根;

直接和上面的代码一样,  输出 gphi(n-1)即可;'

例题3 : POJ 2478  http://poj.org/problem?id=2478

f2= 1,f3 =3 f4=5, f5 =9 f6=11;

而 前10项  φ值为 1 1 2 2 4 2 6 4 6 4   可以发现 f(n)=  从第二项开始 前φ(n)项的和

所以 递推打表 

#include <iostream>
#include <stdio.h>
#include <algorithm>
#include <cmath>
#include <cstring>

using namespace std;
typedef long long ll;
const int N=1000011;
ll phi[N+10];
void iinit()
{
	for(int i=1;i<=N;i++) phi[i]=i;
	for(int i=2;i<=N;i+=2)phi[i]>>=1;
	for(int i=3;i<=N;i+=2){
		if(phi[i]==i)
		{
			for(int j=i;j<=N;j+=i)
				phi[j]=phi[j]-phi[j]/i;
		}
	}
	for(int i=3;i<=N;i++)
		phi[i]+=phi[i-1];
}

int main()
{

    int n;
	iinit();
    while(cin>>n&&n)
    {
    	cout<<phi[n]<<endl;
    }
    return 0;
}