循环神经网络-GRU和LSTM

一、GRU

首先需要明确的是，GRU出现的时间是在LSTM之后的，其实为了简化LSTM而产生的，由于其简易型，一般都会先进行介绍。

首先来看一下RNN的示意图，如下。这里不做解释。

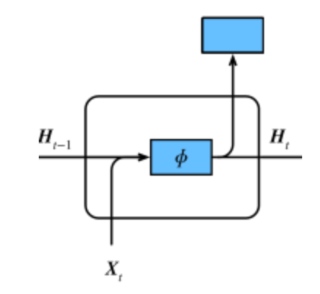
下图是GRU的示意图，相较于RNN似乎复杂了许多。其只是增加了一个cell来存储需要远程传递的信息以及相应的gate来管控信息的传递。

前一层的隐藏状态与本层的输入合在一起分别进入激活函数中，得到重置门R，更新门Z。

随后重置门决定前一层的隐藏状态如何参与本层的输入计算，得到候选隐藏状态。这里重置门的大小主要决定前一层的输出结果与本层的输出结果的关系。

更新门则是决定是否使用候选隐藏状态来更新隐藏状态，还是使用上一层的状态进行传播。这里非此即彼。

事实上，从公式中来观察GRU可能更加易懂。

$R_{t}=\sigma\left(X_{t} W_{x r}+H_{t-1} W_{h r}+b_{r}\right)$
$Z_{t}=\sigma\left(X_{t} W_{x z}+H_{t-1} W_{h z}+b_{z}\right)$
$\widetilde{H}_{t}=\tanh \left(X_{t} W_{x h}+\left(R_{t} \odot H_{t-1}\right) W_{h h}+b_{h}\right)$
$H_{t}=Z_{t} \odot H_{t-1}+\left(1-Z_{t}\right) \odot \widetilde{H}_{t}$

两个门的计算都是根据前一层H和这一层输入X，随后重置门在前一层的H前作为系数，得到候选隐藏状态。这里门的隐藏状态使用sigmoid来得到介于0和1之间的结果，而计算候选隐藏状态使用的激活函数为tanh。

随后则是决定是否使用候选隐藏状态的信息传播，如果不是则传播上一层的隐藏状态。

事实上，在计算的过程中，非此即彼的关系并不明显，因为经过sigmoid计算的结果可能并不等于0，但这样说便于理解。

那为什么需要这么做呢？假设我们在思考英文的句子中，前面的名词的单复数将直接决定句子后面的谓语动词单复数，怎么传递这么远的距离呢？通过GRU，我们可以让有用的信息传递非常远的距离，而对于那些相对来说没用的信息进行屏蔽。

二、LSTM

我们来看LSTM的示意图。这个图相对来说更加复杂了。

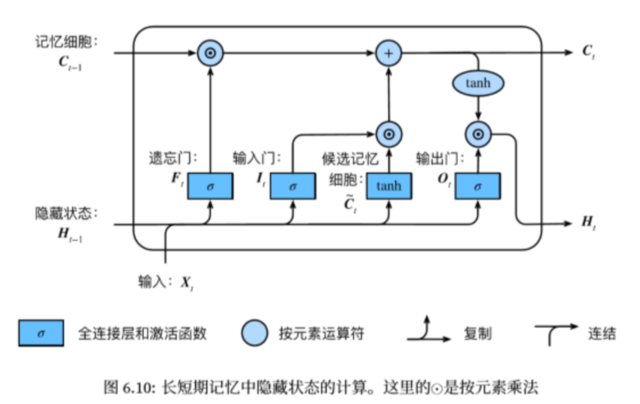
我们直接来看计算公式进行分析。

$I_{t}=\sigma\left(X_{t} W_{x i}+H_{t-1} W_{h i}+b_{i}\right)$
$F_{t}=\sigma\left(X_{t} W_{x f}+H_{t-1} W_{h f}+b_{f}\right)$
$O_{t}=\sigma\left(X_{t} W_{x o}+H_{t-1} W_{h o}+b_{o}\right)$
$\tilde{C}_{t}=\tanh \left(X_{t} W_{x c}+H_{t-1} W_{h c}+b_{c}\right)$
$C_{t}=F_{t} \odot C_{t-1}+I_{t} \odot \tilde{C}_{t}$
$H_{t}=O_{t} \odot \tanh \left(C_{t}\right)$

同样我们通过输入X和前一层传入的隐藏状态输出作为三个门的输入进行计算得到介于0到1之间的结果（sigmoid）。

随后我们计算候选隐藏记忆细胞，这里世界使用上一层的隐藏状态以及输入X（tanh）。

这里的输入门类似于更新门，以决定候选记忆细胞与本层记忆细胞之间的权重关系，同时我们加上遗忘门乘以上一层记忆细胞的结果来把握对上一层输入的权重。

随后我们的使用求得的本层的记忆细胞结果用tanh激活后乘上一个输出门来确定输出的权重。

以上便是对GRU和LSTM的介绍，二者的目的都是想把序列前部分的信息尽可能的向后传递。