数字传输系统信号传输及误码性能分析

2018112800 王天淏

目录

前言

通信原理课程仿真
针对下列两种系统
(1)信道带宽无限时的单极性基带传输
(2)信道带宽受限时的双极性基带传输
采用匹配滤波器(相关接收机)，对误码性能进行仿真:
1.给出系统模型，以及对系统模型的分析，推导误码率理论结果。
2.选择适当仿真工具，搭建仿真模型，设置仿真参数进行仿真并得到误码率仿真结果。
3.将仿真结果与误码率结果进行比较，对误差进行分析得出结论。

以下是本篇文章正文内容

一、概述

1.概述
在数字通信系统中，需要将输入的数字序列映射为信号波形在信道中传输，此时信源输出数字序列，经过信号映射后成为适于信道传输的数字调制信号。由于数字符号是按码元间隔不断产生的，经过讲数字符号一一映射为相应的信号波形后，就形成了数字调制信号。根据映射后信号的频谱特性，可以分成基带信号和频带信号。
数字基带传输系统模型如图1所示。我们把它分成三个模块：发射机、信道、接收机。

数字系统通用模型如下图所示：
在这里插入图片描述

数字基带传输系统模型如下图所示：
在这里插入图片描述

1.1 脉冲调制

脉冲调制框图如下图所示：
在这里插入图片描述
信源的二进制随机序列{\(b_n\)}通过线路编码、窄脉冲生成器和成型滤波器后变为信号波形\(s(t)\)。

1.2 AWGN信道

  • 发射机（脉冲调制模块）产生的发送信号，首先经过信道，再进入接收机。在这门课程里面，我们主要考虑加性高斯白噪声（AWGN）信道，在移动通 信等课程里面，会讨论更为复杂的衰落信道。

  • 我们将讨论两种AWGN信道，即带宽无限的AWGN信道，以及带宽有限的AWGN信道。

带宽无限AWGN信道

信号在进入接收机之前，叠加加性高斯白噪声nw(t)，接收信号为

\[r(t)=s(t)+n_w(t) \]

带宽受限AWGN信道

信道模块的频率传递函数\(C(f)\)类似于理想低通滤波器，其带宽为B。对于这一类信道，发送信号\(s(t)\)通过\(C(f)\)时，其波形及频谱会发生改变。接收信号为

\[r(t)=s(t)*c(t)+n_w(t) \]

1.3 接收机：检测

\(\qquad\qquad\qquad\qquad\qquad\qquad\qquad\)在这里插入图片描述

来自信道的信号波形\(r(t)\)恢复成二进制序列{\({\hat{b}_n}\)}。理想情况下，{\({\hat{b}_n}\)}应该与{\({b_n}\)}完全相同，但由于噪声等影响，会发生误码。

二、信道带宽无限时的单极性基带传输

2.1 系统模型

信道带宽无限时，发送滤波器采用矩形波脉冲。

单极性不归零码(NRZ)

\[i=1, a_1=+A \]

\[i=2, a_2=0 \]

\(\qquad\qquad\qquad\qquad\qquad\)在这里插入图片描述

发送滤波器的冲激响应如下图所示：
\(\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\) 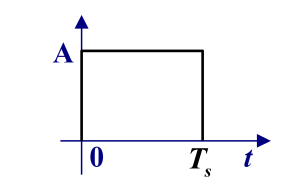在这里插入图片描述

单极性归零码(RZ)

发送序列的幅值ai为：

\[i=1, a_1=+A \]

\[i=2, a_2=0 \]

发送滤波器的冲激响应\(g_T(t)\)是归零脉冲。

2.2 误码性能分析

以单极性不归零码为例：

假设信源等概发送

\[s_i(t)= \begin{cases} s_1(t)=A,\\ s_2(t)=0, \end{cases} \]

经过匹配滤波器接收在这里插入图片描述

\[r(t)=s_i(t)+n_w(t)= \begin{cases} s_1(t)=A+n_w(t),\\ s_2(t)=0+n_w(t), \end{cases} \]

判决量中的噪声：

滤波器输入： $$r(t)=s_i(t)+n_w(t)$$
采样前的信号：$$ y(t)=∫ r( T_b − τ ) h ( τ ) d τ $$
采样值中的噪声： $$Z=∫ n_w( T_b − τ ) h ( τ ) d τ (0,\sigma^2)$$
其中$$\sigma^2=\frac{N_0}{2} E_h=\frac{N_0}{2}E_1=N_0E_b,　E_b=\frac{E_1+E_2}{2}$$
判决量中的有用信号：

最佳抽样时刻\(t=T_b\)时，采样值中的有用信号：$$\int s_i(T_b-\tau)h(\tau){\rm d}x=\int s_i(T_b-\tau)s_1(t-\tau){\rm d}x$$

\[= \begin{cases} E_1,发送s_1,\\ 0,发送s_2 \end{cases}\]

条件概率密度：

\[f(r|s_1)=\frac{1}{\sqrt{2\pi\times\sigma^2}}e^{-\frac{(r-A)^2}{2\sigma^2}} \]

\[f(r|s_2)=\frac{1}{\sqrt{2\pi\times\sigma^2}}e^{-\frac{(r)^2}{2\sigma^2}} \]

\(\qquad\qquad\qquad\qquad\qquad\qquad\)在这里插入图片描述
\(\qquad\)在这里插入图片描述

\(\qquad\)
\(\qquad\)在这里插入图片描述

2.3 仿真模型与仿真过程

clear;close all;
%信道带宽无限时的单极性基带传输
%----------------参数设置------------------
T_start=0;                      %开始时间
T_stop=1;                       %截止时间
T=T_stop-T_start;               %仿真持续时间
T_sample=1/1000;                %采样间隔
f_sample=1/T_sample;            %采样速率
N_sample=T/T_sample;            %采样点数
n=0:N_sample-1;                 %采用序列
r_s=100;                        %传输速率
alpha=0;                        %升余弦系数[df=alpha*rs]
NumBits=T*r_s;                  %传输bit数
NumCoff=40;                     %滤波器阶数
SamplingIns=NumCoff/2;
SamplingStart=NumCoff;

%---------------发送滤波器----------------
g_T=[ones(1,f_sample/r_s),zeros(1,31)]; %发送滤波器，矩形脉冲
b1=(sign(rand(1,NumBits)-0.5)+1)*0.5;   %随机产生0、1等概信号序列
b2=zeros(f_sample/r_s,NumBits);
b2(1,:)=b1;
b3=reshape(b2,1,f_sample/r_s*NumBits);  %原始数字序列
s=conv(b3,g_T);                         %将脉冲序列转换为矩形序列
%-------信道传输时加入加性高斯白噪声--------
N_0=10^(-6);                                    %噪声功率谱
noise_w=wgn(1,length(s),N_0*f_sample,'linear'); %产生白噪声
r=s+noise_w;                                    %叠加白噪声
%------------------接收机------------------
g_R=[ones(1,f_sample/r_s),zeros(1,30)];     %匹配滤波器
y1=conv(r,g_R)/5;                           %接收的波形
%采样序列
sample1=zeros(f_sample/r_s,NumBits);
sample1(1,:)=ones(1,NumBits);
sample2=reshape(sample1,1,f_sample/r_s*NumBits);
sample3=zeros(1,length(y1));
sample3(NumCoff+1:NumCoff+f_sample/r_s*NumBits)=sample2;
y2=y1.*sample3;
y2(:,all(y2==0,1))=[];      %恢复的数字序列
y2(y2<1)=[0];
y3=[0,0,0,y2];
y3=y3(1:length(y3)-3);
C=zeros(9,length(y3));
B=[C;y3];
B=B(:)';
%----------------误码率分析-----------------
b_t=sign(b1);
b_r=sign(y3);
BER=length(find(b_t~= b_r))/NumBits;             %仿真误码率
fprintf('BER=%f \n',BER);
%------------------画图--------------------
myeyediagram=eyediagram(y1(1:length(y1)),f_sample/r_s); %眼图
figure(2);
subplot(311);plot(s);
title('发射器发出信号序列s(t)');
xlabel("Time t (s)");ylabel("Symbol s(t)");
subplot(312);plot(r);
title('传输序列加噪s(t)+n_w(t)');
xlabel("Time t (s)");ylabel("Symbol s(t)+n_w(t)");
subplot(313);plot(y1);
title('接收机获得的信号波形');
xlabel("Time t (s)");ylabel("Symbol y(t)");
% subplot(2,2,4);plot(s);hold on;plot(y1);legend('传输的波形','接受的波形');
figure(3);
subplot(3,1,1);stem(b3,'.');
title('原始信号序列');
xlabel("Time t (s)");ylabel("Symbol \{b_n\}");
subplot(3,1,2);stem(y3,'.');
title('接收数字序列');
xlabel("Time t (s)");ylabel("Symbol \{b_n'\}");
subplot(3,1,3);stem(b3,'.');hold on;stem(B,'.');legend('原始数字序列','接收数字序列');
title('原始与接收数字序列对比');
xlabel("Time t (s)");ylabel("Symbol \{b_n\} and \{b_n'\}");

sn=0.1:0.01:100;                            %定义信噪比序列
snlg=20*log10(sn);                          %将信噪比转化为dB表示
ssingle=sqrt(sn/2);
bsingle=erfc(ssingle)/sqrt(2);              %求单极性的误比特率序列

figure(4);
semilogy(snlg,bsingle);
axis([-20 30 0.0000001 1]);
title('NRZ');
xlabel('输单极性不归零码入信噪比');
ylabel('误比特率')

运行结果如下：
在这里插入图片描述

\(\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\)单极性不归零码-调制解调波形
在这里插入图片描述
\(\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\)单极性不归零码-原始信号与接受序列比较
在这里插入图片描述\(\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\)单极性码接收信号眼图
\(\qquad\qquad\qquad\qquad\qquad\qquad\qquad\)在这里插入图片描述

\(\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad\qquad\qquad\)单极性不归零码基带传输−仿真误码率
\(\qquad\qquad\quad\quad\quad\quad\)

在这里插入图片描述

\(\qquad\qquad\qquad\qquad\qquad\quad\quad\quad\quad\quad\qquad\qquad\) 单极性不归零码基带传输−理论误码率曲线

三、信道带宽受限的双极性基带传输

3.1 系统模型

双极性不归零码

发送序列的幅值ai为：

\[i=1, a_1=+A \]

\[i=2, a_2=-A \]

发送滤波器的冲激响应为不归零脉冲。

双极性归零码

发送序列的幅值ai为：

\[i=1, a_1=+A \]

\[i=2, a_2=-A \]

发送滤波器的冲激响应为归零脉冲。

当信道的带宽受限时，可以采用升余弦信号作为发送滤波器
\(\qquad\qquad\qquad\) 在这里插入图片描述

3.2 误码性能分析

以双极性不归零码为例：

假设信源等概发送

\[s_i ( t ) = \begin{cases} s 1 ( t ) = + A ,\\ s 2 ( t ) = − A , \end{cases}\]

经过匹配滤波器接收

\[r(t)=s_i(t)\times c(t)+n_w(t) \]

假定发送s1(t):
匹配滤波器的输入：$$r(t)=s_1(t)+n_w(t)$$
匹配滤波器输出（采样前的信号）：$$ \int_{-\infty}^{+\infty}{r(t-τ)h(τ)} ,{\rm d}τ$$
​
最佳抽样时刻\(t=T_b\)处，采样值中的有用信号:

\[\int_{-\infty}^{+\infty}{s_1(T_b-τ)s_1(T_b-τ)}\,{\rm d}τ=Eb \]

\(E_b\)是平均比特能量，\(E_b=E_1=E_2\)

采样值中的噪声:$$Z=\int_{-\infty}^{+\infty}{n_w(T_b-τ)h(τ)},{\rm d}τ\sim N(0,σ^2)$$其中

\[σ^2=\frac{N_0E_b}{2} \]

发送s1(t)条件下的判决量为\(y=y(T_b)=E_b+Z\)。\(y\)是均值为\(E_b\)、方差为\(σ^2\)的高斯随机变量，其概率密度函数为

\[p_1(y)=p(y|s1)=\frac{1}{\sqrt{2\pi\sigma^2}}\quad e^{-\frac{(y+E_b)^2}{2\sigma^2}} \]

发送s1(t)，如果判决量y低于门限\(V_T\)，则判决出错，$$P(e|s_1)=P(Y<V_T|s_1)=\int_{-\infty}^{V_T}{p_1(y)},{dy}$$

\(\qquad\qquad\qquad\qquad\qquad\qquad\)在这里插入图片描述
发送s2(t)同理。
因此等概时的平均误比特率：

\[P_b=\frac{1}{2}P(e|s_1)+\frac{1}{2}P(e|s_2)=\frac{1}{2}erfc(\sqrt\frac{E_b}{N_0})=Q(\sqrt\frac{2E_b}{N_0}) \]

3.3 仿真模型与仿真过程

clear;close all;
%带宽受限，双极性不归零码传输
%-------参数设置--------
T_start=0;                      %开始时间
T_stop=1;                       %截止时间
T=T_stop-T_start;               %仿真持续时间
T_sample=1/1000;                %采样间隔
f_sample=1/T_sample;            %采样速率
N_sample=T/T_sample;            %采样点数
n=0:N_sample-1;                 %采样序列
r_s=100;                        %传输速率
alpha=0.25;                     %升余弦滚降系数
                                %df=alpha*rs=25Hz
NumBits=T*r_s;                  %传输bit数
NumCoff=30;                     %滤波器阶数
SamplingIns=NumCoff/2;          
SamplingStart=NumCoff;

%----------信号发生器-------------
g_T=firrcos(NumCoff,r_s/2,alpha*r_s,f_sample);          %升余弦滤波器
b1=sign(rand(1,NumBits)-0.5);                           %原始0、1数字序列
b2=zeros(f_sample/r_s,NumBits);
b2(1,:)=b1;
b3=reshape(b2,1,f_sample/r_s*NumBits);                  %原始数字序列
s=conv(b3,g_T);                                         %发送的信号波形
%-------AWGN高斯信道-------
%加入高斯白噪声
N_0=10^(-6);                                             %功率谱密度
noise_w=wgn(1,length(s),N_0*f_sample,'linear');          %产生白噪声
r=s+noise_w;                                             %叠加白噪声
%----------接收机------------
g_R=firrcos(NumCoff,r_s/2,alpha*r_s,f_sample);      %升余弦滤波器（MF）
y1=conv(r,g_R);                                     %接收的波形
sample1=zeros(f_sample/r_s,NumBits);
sample1(1,:)=ones(1,NumBits);
sample2=reshape(sample1,1,f_sample/r_s*NumBits);
sample3=zeros(1,length(y1));
sample3(NumCoff+1:NumCoff+f_sample/r_s*NumBits)=sample2;
y2=y1.*sample3;
y2(:,all(y2==0,1))=[];                              %恢复的数字序列
C = zeros(9,length(y2));
B = [C;y2];
B = B(:)';
%------------误码率---------
b_t=(sign(b1)+1)*0.5;
b_r=(sign(y2)+1)*0.5;
BER=length(find(b_t~= b_r))/NumBits;    %仿真误码率
fprintf('BER=%f \n',BER);
%--------------作图-----------
myeyediagram=eyediagram(y1(1:length(y1)),f_sample/r_s);%眼图
figure(2);
subplot(311);plot(s);
title('发射器发出信号序列s(t)');
xlabel("Time t (s)");ylabel("Symbol s(t)");
subplot(312);plot(r);
title('传输序列加噪s(t)+n_w(t)');
xlabel("Time t (s)");ylabel("Symbol s(t)+n_w(t)");
subplot(313);plot(y1);
title('接收机获得的信号波形');
xlabel("Time t (s)");ylabel("Symbol y(t)");
% subplot(2,2,4);plot(s);hold on;plot(y1);legend('传输的波形','接受的波形');

figure(3);
subplot(3,1,1);stem(b3,'.');
title('原始信号序列');
xlabel("Time t (s)");ylabel("Symbol \{b_n\}");
subplot(3,1,2);stem(y2,'.');
title('接收数字序列');
xlabel("Time t (s)");ylabel("Symbol \{b_n'\}");
subplot(3,1,3);stem(b3,'.');hold on;stem(5*B,'.');legend('原始数字序列','恢复的数字序列');
title('原始与接收数字序列对比');
xlabel("Time t (s)");ylabel("Symbol \{b_n\} and \{b_n'\}");

sn=0.1:0.01:100;                                    %定义信噪比序列
snlg=20*log10(sn);                                  %将信噪比转化为dB表示
sdouble=sqrt(sn);
bdouble=erfc(sdouble)/sqrt(2);                      %求双极性的误比特率序列
figure(4);
semilogy(snlg,bdouble);
axis([-20 30 0.0000001 1]);
title('双极性不归零码NRZ');
xlabel('输入信噪比/dB');
ylabel('误比特率')

运行结果：

在这里插入图片描述
\(\qquad\qquad\qquad\qquad\qquad\qquad\quad\qquad\qquad\qquad\)双极性不归零码-调制解调波形
在这里插入图片描述
\(\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\)双极性不归零码-数字序列
在这里插入图片描述
\(\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\)双极性码接收信号眼图
\(\qquad\qquad\qquad\)在这里插入图片描述

\(\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\)双极性不归零码-理论误码率

四、信道带宽受限的QPSK传输

4.1 系统模型

QPSK有4个可能的离散相位状态，每个载波相位携带两个二进制符号，将这四个相位设计为间隔π/2的均匀相位。
QPSK（四进制移相键控）信号的产生与解调

对于a图形式的QPSK：\(\theta_i=(2i-1)*\frac{\pi}{4}\)
对于b图形式的QPSK：\(\theta_i=(i-1)*\frac{\pi}{2}\)
QPSK的产生：

\[s_i(t)=Acos(w_ct+\theta_i)=A(cos\theta_i *cosw_ct-sin\theta_i *sinw_ct) \]

\[s_i(t)=A[I(t)cosw_ct-Q(t)sinw_ct] \]

\[I(t)=cos\theta_i;Q(t)=sin\theta_i\quad 0\leq t\leq T_s \]

\(\qquad\qquad\qquad\qquad\qquad\)在这里插入图片描述
\(\qquad\qquad\qquad\)在这里插入图片描述
\(\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad　　　　　　　　　　\)正交调制原理图
QPSK信号，功率谱密度
\(\qquad\qquad\qquad\)在这里插入图片描述
\(\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad　　　　　　　　　　\)QPSK信号功率谱密度图

发送端:

首先产生一串比特流，经过串并变换，分为两路(\(I\) 路和\(Q\)路)，奇数进I路并与\(cos(w_ct)\)相乘、偶数进\(Q\)路并与\(sin(w_ct)\)相乘，然后\(I\)路信号减\(Q\)路信号即可得到QPSK信号。

\(\qquad\qquad\qquad\)在这里插入图片描述
　　　　　　　　　　　　　　　　　　　　　　　QPSK相关解调器最佳接收

接收端:

\(\qquad\) ( 基本不考虑带通滤波器，只让\(w_c\)载波进入)接收端接到信号分别进入\(I\)路和\(Q\)路, \(I\)路与\(cos(w_ct)\)相乘、 \(Q\)路与\(-sin(w_ct)\)相乘， 相乘后通过低通滤波器、抽样判决，还原为原来的\(I\)路和\(Q\)路信息，然后通过并/串变换变成比特流。这时候比较该比特流与发送端产生的比特流..\([a_k,b_k]\)..到底错了多少比特。
\(\qquad\)这次实验是了解并仿真以上每个步骤对应的波形，该实验用积分器代替了接收端的载波恢复、低通滤波器、抽样判决对应的功能及式子。

4.2 误码性能分析

\(\quad\)由于QPSK信号可看作同相及正交支路2PSK的叠加，所以在解调时可对两路信号分别进行2PSK的解调，然后进行并串变换，得到所传输的数据。计算QPSK解调的误比特率有两种办法：一是先计算误符率（平均判错四进制符号的概率），然后再根据误符率计算从四进制符号译为二进制符号的误比特率；另一计算方法是沿用2PSK匹配滤波器的误比特率计算公式。下面采用第二种方法进行计算。
\(\quad\)\(I\)路功率是QPSK功率(\(\frac{A^2}{2}\))的一半,为\(\frac{A^2}{4}\),\(I\)路比特周期是QPSK比特周期\(T_b\)的二倍，为\(2T_b\)。\(I\)路比特能量是\(\frac{A^2}{4}*2T_b=E_b\),与QPSK的比特能量相同。在给定QPSK发端信源输出的二进制符号“1”和“0”等概出现，二进制码元经串并变换后在同向支路及正交支路也是等概分布的，所以在收端的同向及正交支路解调的输出经并串变换后的数据，其总的平均误比特率与\(I\)支路及Q\(支路\)的 平均错判概率为

\[P_{eI}=P_{eQ}=\frac{1}{2}[\sqrt{\frac{(\frac{A^2}{2})(2T_b)}{2N_0}}]=\frac{1}{2}erfc(\sqrt\frac{E_b}{N_0}) \]

4.3 仿真模型与仿真过程

1.发送端产生的比特流\(...[a_k,b_k]...\)，奇数进I路、偶数进Q路对应的比特数和波形图如下所示

在这里插入图片描述
\(\qquad\qquad\qquad\)在这里插入图片描述
用matlab仿真出来的波形图与表格数据一致。

2.QPSK调制乘以载波信号后传输的I路和Q路、IQ路和信号(QPSK) 对应波形图如图所示

在这里插入图片描述

3.QPSK经过解调产生的二进制信息比特流、I 路和Q路信息波形图如图所示

\(\qquad\qquad\qquad\)在这里插入图片描述

clear all;clc;
N=20;%比特数
T=1;%比特周期
fc=2;%载波频率
Fs=100;%抽样频率
bitstream=randi([0,1],1,N);%随机产生的比特数0、1
bitstream=2*bitstream-1;%单极性变为双极性（0到-1；1到1）
I=[];Q=[];
%奇数进I路,偶数进Q路
for i=1:N
    if mod(i,2)~=0
        I=[I,bitstream(i)];
    else
        Q=[Q,bitstream(i)];
    end
end
%采用绘图比较I、Q比特流
bit_data=[];
for i=1:N
    bit_data=[bit_data,bitstream(i)*ones(1,T*Fs)];%在一个比特周期里面有T*Fs个1和采样点一模一样
end
I_data=[];Q_data=[];
for i=1:N/2
    %I路和Q路是原来比特周期的两倍,2Tb=Ts(码元周期)，因此采样点个数为T*Fs*2
    I_data=[I_data,I(i)*ones(1,T*Fs*2)];
    Q_data=[Q_data,Q(i)*ones(1,T*Fs*2)];
end
%绘图
figure();
%时间轴
t=0:1/Fs:N*T-1/Fs;
subplot(3,1,1)
plot(t,bit_data);legend('Bitstream')%比特信息
subplot(3,1,2)
plot(t,I_data);legend('I Bitstream')%I路信息
subplot(3,1,3)
plot(t,Q_data);legend('Q Bitstream')%Q路信息
%载波信号
bit_t=0:1/Fs:2*T-1/Fs;%载波周期为2倍比特周期,定义时间轴
%定义I路和Q路的载波
I_carrier=[];Q_carrier=[];
for i=1:N/2
    I_carrier=[I_carrier,I(i)*cos(2*pi*fc*bit_t)];%I路载波信号
    Q_carrier=[Q_carrier,Q(i)*cos(2*pi*fc*bit_t+pi/2)];%Q路载波信号
end
%传输信号
QPSK_signal=I_carrier+Q_carrier;
%绘图
figure();%产生一个新图
subplot(3,1,1)
plot(t,I_carrier);legend('I signal')%I路信号
subplot(3,1,2)
plot(t,Q_carrier);legend('Q signal')%Q路信号
subplot(3,1,3)
plot(t,QPSK_signal);legend('QPSK signal')%I路、Q路和的信号
snr=1;%信躁比
%接收信号
QPSK_receive=awgn(QPSK_signal,snr);%awgn()添加噪声
%解调
for i=1:N/2
    I_output=QPSK_receive(1,(i-1)*length(bit_t)+1:i*length(bit_t)).*cos(2*pi*fc*bit_t);
    if sum(I_output)>0 %积分器求和，大于0为1，否则为-1
        I_recover(i)=1;
    else
        I_recover(i)=-1;
    end
     Q_output=QPSK_receive(1,(i-1)*length(bit_t)+1:i*length(bit_t)).*cos(2*pi*fc*bit_t+ pi/2);
    if sum(Q_output)>0
        Q_recover(i)=1;
    else
        Q_recover(i)=-1;
    end
end
%并/串变换
bit_recover=[];
for i=1:N
    if mod(i,2)~=0
        bit_recover=[bit_recover,I_recover((i-1)/2+1)];%奇数取I路信息
    else
        bit_recover=[bit_recover,Q_recover(i/2)];%偶数取Q路信息
    end
end
%适用绘图比较I、Q比特流
recover_data=[];
for i=1:N
    recover_data=[recover_data,bit_recover(i)*ones(1,T*Fs)];
end
I_recover_data=[];Q_recover_data=[];
for i=1:N/2
    I_recover_data=[I_recover_data,I_recover(i)*ones(1,T*Fs*2)];
    Q_recover_data=[Q_recover_data,Q_recover(i)*ones(1,T*Fs*2)];
end
%绘图
figure();
t=0:1/Fs:N*T-1/Fs;
subplot(3,1,1)
plot(t,recover_data);legend('Bitstream')%恢复的比特信息
subplot(3,1,2)
plot(t,I_recover_data);legend('I Bitstream')%恢复的I路信息
subplot(3,1,3)
plot(t,Q_recover_data);legend('Q Bitstream')%恢复的Q路信息

五、信道带宽受限的16QAM传输

5.1 系统模型

MQAM信号表达式

\[s_QAM(t)=a_{i_c}g_T(t)cosw_ct-a_{i_s}g_T(t)sinw_ct\quad i=1,2,...,M\quad 0\leq t\leq T_s \]

式中\(\{a_{i_c}\}\)及\(\{a_{i_s}\}\)是一组离散电平的集合，\(g_T(t)\)是基带成形滤波器的冲激响应
\(\qquad\qquad\qquad\qquad\)在这里插入图片描述
\(\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\qquad\)MQAM基带传输的系统模型

5.2 误码性能分析

矩形星座QAM的最佳接收误符率与MASK的一样，取决于数字基带MPAM的误符率。MQAM的正确判决符号的概率为

\[P_c=(1-P_{\sqrt{M}})^2 \]

式中，\(P_{\sqrt{M}}\)表示同相或正交支路\(\sqrt{M}\)进制ASK的误符率，该\(\sqrt{M}\)进制ASK的平均功率是MQAM信号总的平均功率\(P_s\)的一半，即

\[P_{\sqrt{M}}=2(1-\frac{1}{\sqrt{M}})Q[\sqrt{\frac{3P_sT_s}{(M-1)N_0}}] \]

\[\qquad =2(1-\frac{1}{\sqrt{M}})Q[\sqrt{\frac{3E_s}{(M-1)N_0}}] \]

\[\qquad=2(1-\frac{1}{\sqrt{M}})Q[\sqrt{\frac{3log_2M*E_b}{(M-1)N_0}}] \]

\[=2(1-\frac{1}{\sqrt{M}})Q[\sqrt{\frac{d^2_{min}}{2N_0}}] \]

MQAM信号的误符率为

\[P_M=1-P_c=1-(1-P_{\sqrt{M}})^2=2P_{\sqrt{M}}-P^2_{\sqrt{M}} \]

MQAM的误符率曲线如图

\(\qquad\qquad\qquad\qquad\qquad\quad\)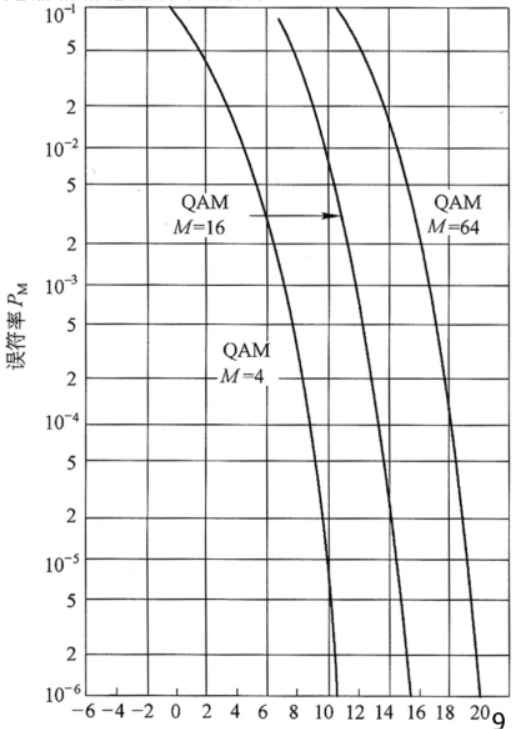
\(\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\qquad\) 16QAM和64QAM的误符率曲线

5.3 仿真模型与仿真过程

clc;clear all;close all;
nsymbol=100000;%表示一共有多少个符号，这里定义100000个符号
M=16;%M表示QAM调制的阶数,表示16QAM，16QAM采用格雷映射(所有星座点图均采用格雷映射)
N=64;
%格雷映射编码规则
graycode=[0 1 3 2 4 5 7 6 12 13 15 14 8 9 11 10];
%格雷映射十进制的表示
graycode1=[0 1 3 2 6 7 5 4 8 9 11 10 14 15 13 12 24 25 27 26 30 31 29 28 16 17 19 18 22 23 21 20 48 49 51 50 54 55 53 52 56 57 59 58 62 63 61 60 40 41 43 42 46 47 45 44 32 33 35 34 38 39 37 36];
EsN0=5:20;%信噪比范围
snr1=10.^(EsN0/10);%将db转换为线性值
%0到15之间随机产生一个数,数的个数为：1乘nsymbol，得到原始数据
msg=randi([0,M-1],1,nsymbol);
%对数据进行格雷映射
msg1=graycode(msg+1);
%调用matlab中的qammod函数，16QAM调制方式的调用(输入0到15的数，M表示QAM调制的阶数)得到调制后符号
msgmod=qammod(msg1,M);
%调用matlab中的scatterplot函数,画星座点图
scatterplot(msgmod);
%取a+bj的模.^2得到功率除整个符号得到每个符号的平均功率
spow=norm(msgmod).^2/nsymbol;
%64QAM
nsg=randi([0,N-1],1,nsymbol);
nsg1=graycode1(nsg+1);
nsgmod=qammod(nsg1,N);
%调用matlab中的scatterplot函数,画星座点图
scatterplot(nsgmod);
spow1=norm(nsgmod).^2/nsymbol;

for i=1:length(EsN0)
    sigma=sqrt(spow/(2*snr1(i)));%16QAM根据符号功率求出噪声的功率
    sigma1=sqrt(spow1/(2*snr1(i)));%64QAM根据符号功率求出噪声的功率
    %16QAM混入高斯加性白噪声
    rx=msgmod+sigma*(randn(1,length(msgmod))+1i*randn(1,length(msgmod)));
    %64QAM混入高斯加性白噪声
    rx1=nsgmod+sigma*(randn(1,length(nsgmod))+1i*randn(1,length(nsgmod)));
    %16QAM的解调
    y=qamdemod(rx,M);
    %64QAM的解调
   y1=qamdemod(rx1,N);
   decmsg=graycode(y+1);%16QAM接收端格雷逆映射，返回译码出来的信息，十进制
   decnsg=graycode1(y1+1);%64QAM接收端格雷逆映射
   %一个符号四个比特，比较发送端信号msg和解调信号decmsg转换为二进制，ber(i)错误的比特率
   [err1,ber(i)]=biterr(msg,decmsg,log2(M));
   [err2,ser(i)]=symerr(msg,decmsg);%16QAM求实际误码率
   [err1,ber1(i)]=biterr(nsg,decnsg,log2(N));
   [err2,ser1(i)]=symerr(nsg,decnsg);%64QAM求实际误码率
end
%16QAM
scatterplot(rx);%调用matlab中的scatterplot函数,画rx星座点图
p = 2*(1-1/sqrt(M))*qfunc(sqrt(3*snr1/(M-1)));
ser_theory=1-(1-p).^2;%16QAM理论误码率
ber_theory=1/log2(M)*ser_theory;

%64QAM
scatterplot(rx1);
p1=2*(1-1/sqrt(N))*qfunc(sqrt(3*snr1/(N-1)));
ser1_theory=1-(1-p1).^2;%64QAM理论误码率
ber1_theory=1/log2(N)*ser1_theory;%得到误比特率

%绘图
figure()
%使用 y 轴的以 10 为基数的对数刻度和 x 轴的线性刻度创建一个绘图
semilogy(EsN0,ber,"o", EsN0, ser, "*",EsN0, ser_theory, "-", EsN0, ber_theory, "-");
title("16-QAM载波调制信号在AWGN信道下的误比特率性能")
xlabel("EsN0");
ylabel("误比特率和误符号率");
legend("误比特率", "误符号率","理论误符号率","理论误比特率");
%阶数不同,16和64QAM调制信号在AWGN信道的性能比较
figure()
semilogy(EsN0,ser_theory,'o',EsN0,ser1_theory,'o');%ber ser比特仿真值 ser1理论误码率 ber1理论误比特率
title('16和64QAM调制信号在AWGN信道的性能比较');grid;
xlabel('Es/N0(dB)');%性躁比
ylabel('误码率');%误码率
legend('16QAM理论误码率','64QAM理论误码率');

\(\qquad\qquad\qquad\qquad\qquad\quad\)在这里插入图片描述
\(\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad\) 16QAM的星座点图
\(\qquad\qquad\qquad\qquad\qquad\quad\)在这里插入图片描述
\(\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad\) 64QAM的星座点图
\(\qquad\qquad\qquad\qquad\qquad\quad\)在这里插入图片描述
\(\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad\quad\) 16QAM加噪声后的星座点图

\(\qquad\qquad\qquad\qquad\qquad\quad\)在这里插入图片描述
\(\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad\) 64QAM加噪声后的星座点图
\(\qquad\qquad\qquad\qquad\)在这里插入图片描述
\(\qquad\qquad\qquad\qquad\qquad\qquad\qquad\) 16-QAM载波调制信号在AWGN信道下的误比特率性能比较
\(\qquad\qquad\qquad\qquad\)在这里插入图片描述
\(\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad\) 16和64QAM调制信号在AWGN信道的性能比较
结论
由图可知，在同一个性躁比条件下，64QAM比16QAM的误码率更高，因此可以得出普遍的结论，阶数越高，误码率越高。

总结

\(\quad\)通过本次的仿真实验可以得出，数字信号基带传输系统的构建与传输信道的带宽有着密切的联系，当信道带宽无限时，信号传输使用的为矩形脉冲，即成型滤波器为矩形不归零脉冲，输出的信号进入信道会收到加性高斯白噪声的干扰，接收端可以采用低通滤波器与匹配滤波器，为得到最小的平均误比特率，一般采用匹配滤波器作为最佳接收。
\(\qquad\)当信道中信噪比减小时，眼图波动增大，“眼睛”张开的程度减弱。单极性码与双极性相比，双极性码的平均误比特率比单极性的更小。16QAM的编码效率比QPSK高，但容错性不如QPSK好。16QAM与64QAM相比，16QAM的误码性能更优。
posted @ 2021-01-18 01:35  四有  阅读(2011)  评论(0)    收藏  举报