DGP初探之Geometry Image
2010-05-29 15:59 六水 阅读(1578) 评论(1) 编辑 收藏 举报
先发个刚完成的图
如右图所示,有了geometry image后,就可以用类似生成地形的方法来重构模型了。
大概侃侃Geometry Image
现在DGP(Digital Geometry Proccesing)方面成熟的算法应该要数子分网格法了。
对于我这初学者来说,它整个流程还算是比较复杂的,需要先按照拓扑约束进行
分区,形成Voronoi图,然后根据其对偶图生成Delaunay三角剖分(基网格),接着
还要使用调和映射把每个三角形区域内的所有顶点嵌入对应的三角形内部,生成
初始参数化...具体不是几句话能说清楚了的。
现在我在尝试的是Geometry Image的方法,该方法是2002年提出的,擅长做压缩
但由于它构成过程中需要对模型进行大量切割,结果会生成大量不连续的边界,这
限制了它在很多领域的使用。譬如如果要做信号滤波,就不能使用现有的图像滤波
技术了。
尽管如此,我还是觉得这种技术很有趣,毕竟Geometry Image更加容易用GPU来
处理。接下来可能会做做一些有趣的试验,发掘一下它的好处。
试验日志
我现在还停留在Geometry Image的生成上。
主要精力都耗在展开网格上了。开始的时候我找找能处理任意亏格的模型的方法,后
来也找到了几个,发现也读不懂,于是我重新去读了读拓扑学基础,又看了看
微分几何,对拓扑流形,网格映射等有一定了解后,看起论文来舒服多了。很快
就开始写程序了,简单起见,试验中我使用了很简单的模型,亏格为0,模型上开了一
个口,方便展开。这里我是使用了Harmonic Mapping的方法,在这里要谢谢网友同山,
跟我提到了与Harmonic Mapping相关的重心映射的方法,然后在一篇相关的论文里找
到了完整的计算公式。
应用这公式,求解每个顶点对应的参数坐标,其实就是解线性方程组。一开始是使用矩
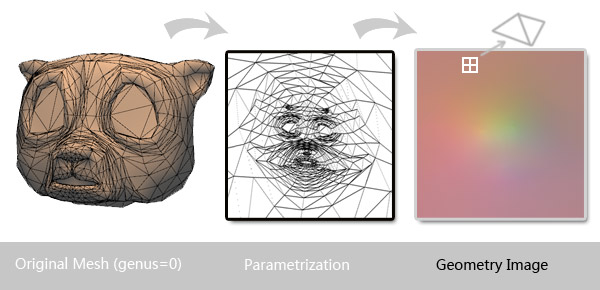
阵求逆的方法来解,还是顺利地做出来了。如顶上那图的中间那小图。
关于参数化的形变
参数化过程引入的形变一直都是我们非常关心的问题。我现在做的这个,尽管是使用了
调和映射,已经尽最大限度最小化了形变,但形变还是很大的,主要是参数化后网格密
度很不均匀,这意味着网格密度变化的区域对应的三角形形变很厉害。为了尽量降低这
种形变带来的坏处,我们在采样的时候尝试使用了非均匀采样,根据网格的密度调整了
采样网格的分布。结果是比均匀采样好一点,但也不理想。
关于加速求大规模解线性方程组
后来又测试了比较大的模型,顶点比较多,用矩阵求逆的方法就非常的慢了,毕竟这个
矩阵是nxn的(n为网格内部顶点的个数)。不过,这个矩阵是稀疏矩阵,想起以前上线数
的印象,有快速的方法的。去找了找相关的方法,最终还是用到了数值分析里介绍的迭
代法。开始看到的是Jacobi迭代法,对矩阵的要求是对角占优,我现在的矩阵并非严格
的对角占优,算是弱对角占优吧,于是也去尝试一下。后来发现真的不行,迭代了很多
次都没有收敛,无法解出近似解。接着只能尝尝别的方法了,Gauss-Seidel迭代法,其实
也就是Jacobi的拓展,嘿,发现它还真收敛了,不过收敛得也太慢了。我都迭代了几千次
了。还是不行,再用用松弛因子的方法,我的矩阵也刚好符合超松弛法的条件,于是加上
去,其实它也就是比Gauss-Seidel多了个松弛因子w罢了。后来发现,在方程了加了个w,
其实就是三种方法的统一了,0<w<1就是低松弛法,w=1就是Gauss-Seidel法,1<w<2
就是超松弛法了。
测试结果,嗯,算是收敛得比较快了,不过对于顶点比较多的模型,我现在还得迭代上千
次,整个求解过程需要耗时0.3秒左右。
还得继续提速啊。。。
回到起点,革命尚未完成
在我搞Geometry Image前,主要是想把一个模型的网格均匀化。在网上也没找到现成的
工具,于是也只有自己去写了。不过,我现在写的程序还是没能达到要求,实验效果, 如
上图所示,网格也没有想象中的那么均匀,应该就是参数化或重采样的问题了。
另外,精度也是问题,从效果来看,有许多细节也丢失了,如果要不丢失细节,那要生成很
细的网格,顶点增大不少。接下来可能做做自适应采样。
如右图所示,有了geometry image后,就可以用类似生成地形的方法来重构模型了。
大概侃侃Geometry Image
现在DGP(Digital Geometry Proccesing)方面成熟的算法应该要数子分网格法了。
对于我这初学者来说,它整个流程还算是比较复杂的,需要先按照拓扑约束进行
分区,形成Voronoi图,然后根据其对偶图生成Delaunay三角剖分(基网格),接着
还要使用调和映射把每个三角形区域内的所有顶点嵌入对应的三角形内部,生成
初始参数化...具体不是几句话能说清楚了的。
现在我在尝试的是Geometry Image的方法,该方法是2002年提出的,擅长做压缩
但由于它构成过程中需要对模型进行大量切割,结果会生成大量不连续的边界,这
限制了它在很多领域的使用。譬如如果要做信号滤波,就不能使用现有的图像滤波
技术了。
尽管如此,我还是觉得这种技术很有趣,毕竟Geometry Image更加容易用GPU来
处理。接下来可能会做做一些有趣的试验,发掘一下它的好处。
试验日志
我现在还停留在Geometry Image的生成上。
主要精力都耗在展开网格上了。开始的时候我找找能处理任意亏格的模型的方法,后
来也找到了几个,发现也读不懂,于是我重新去读了读拓扑学基础,又看了看
微分几何,对拓扑流形,网格映射等有一定了解后,看起论文来舒服多了。很快
就开始写程序了,简单起见,试验中我使用了很简单的模型,亏格为0,模型上开了一
个口,方便展开。这里我是使用了Harmonic Mapping的方法,在这里要谢谢网友同山,
跟我提到了与Harmonic Mapping相关的重心映射的方法,然后在一篇相关的论文里找
到了完整的计算公式。
应用这公式,求解每个顶点对应的参数坐标,其实就是解线性方程组。一开始是使用矩
阵求逆的方法来解,还是顺利地做出来了。如顶上那图的中间那小图。
关于参数化的形变
参数化过程引入的形变一直都是我们非常关心的问题。我现在做的这个,尽管是使用了
调和映射,已经尽最大限度最小化了形变,但形变还是很大的,主要是参数化后网格密
度很不均匀,这意味着网格密度变化的区域对应的三角形形变很厉害。为了尽量降低这
种形变带来的坏处,我们在采样的时候尝试使用了非均匀采样,根据网格的密度调整了
采样网格的分布。结果是比均匀采样好一点,但也不理想。
关于加速求大规模解线性方程组
后来又测试了比较大的模型,顶点比较多,用矩阵求逆的方法就非常的慢了,毕竟这个
矩阵是nxn的(n为网格内部顶点的个数)。不过,这个矩阵是稀疏矩阵,想起以前上线数
的印象,有快速的方法的。去找了找相关的方法,最终还是用到了数值分析里介绍的迭
代法。开始看到的是Jacobi迭代法,对矩阵的要求是对角占优,我现在的矩阵并非严格
的对角占优,算是弱对角占优吧,于是也去尝试一下。后来发现真的不行,迭代了很多
次都没有收敛,无法解出近似解。接着只能尝尝别的方法了,Gauss-Seidel迭代法,其实
也就是Jacobi的拓展,嘿,发现它还真收敛了,不过收敛得也太慢了。我都迭代了几千次
了。还是不行,再用用松弛因子的方法,我的矩阵也刚好符合超松弛法的条件,于是加上
去,其实它也就是比Gauss-Seidel多了个松弛因子w罢了。后来发现,在方程了加了个w,
其实就是三种方法的统一了,0<w<1就是低松弛法,w=1就是Gauss-Seidel法,1<w<2
就是超松弛法了。
测试结果,嗯,算是收敛得比较快了,不过对于顶点比较多的模型,我现在还得迭代上千
次,整个求解过程需要耗时0.3秒左右。
还得继续提速啊。。。
回到起点,革命尚未完成
在我搞Geometry Image前,主要是想把一个模型的网格均匀化。在网上也没找到现成的
工具,于是也只有自己去写了。不过,我现在写的程序还是没能达到要求,实验效果, 如
上图所示,网格也没有想象中的那么均匀,应该就是参数化或重采样的问题了。
另外,精度也是问题,从效果来看,有许多细节也丢失了,如果要不丢失细节,那要生成很
细的网格,顶点增大不少。接下来可能做做自适应采样。