DS博客作业05--查找
0.PTA得分截图

1.本周学习总结(0-4分)
1.1 总结查找内容
1.1.1查找的性能指标ASL(平均查找长度)
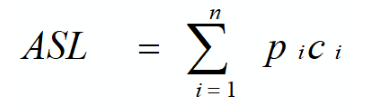
ASL越大,时间性能越差;反之,时间性能越好
n:表中元素个数
pi:查找第i个记录的概率 (通常认为pi = 1/n,每个元素查找概率相同)
ci:找到第i个记录所需要的关键字比较次数
1.1.2静态查找
1、顺序查找
从线性表一端开始,遍历线性表,若遍历到某个关键字的值和给定值相等,则成功查找到;
如果遍历完线性表后,还是没找到关键字的值和给定值相等,则失败
结构体
#define MAX 最大个数
typedef struct
{
关键字的数据类型 key;
其他数据
} NodeType;
typedef NodeType SeqList[MAXL]; //顺序表
查找
while (i<count && s[i].key!=num)//从线性表一端开始,遍历线性表
i++;
if (i>=n)//未找到
2、二分(折半)查找
(线性表中关键字的值应按照递增或递减顺序排列)
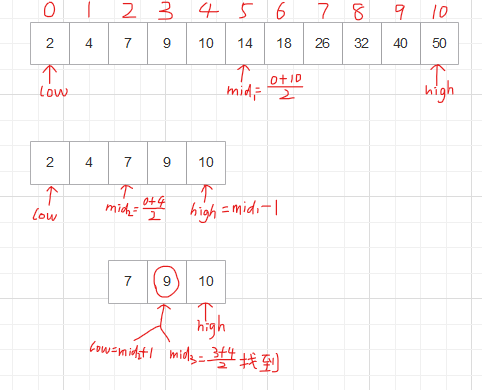
while (low<=high) //当前区间存在元素时循环
{
mid=(low+high)/2;//取下限
if (s[mid].key==num)//查找成功
return mid+1;
if (num<s[mid].key)//需要查找的数据num小于当前中值
high=mid-1;
else//需要查找的数据num大于当前中值
low=mid+1;
}
1.1.3动态查找
1、二叉排序(查找)树
特点:
没有相同关键字的节点
中序遍历二叉排序(查找)树得到一个关键字的递增或递减有序序列
空树也是二叉排序(查找)树!
左、右子树也都是二叉排序(查找)树
一般默认(具体按照题意):
若左子树不空,则左子树上所有结点的值均小于根结点的值
若右子树不空,则右子树上所有结点的值均大于根结点的值
二叉排序(查找)树操作集
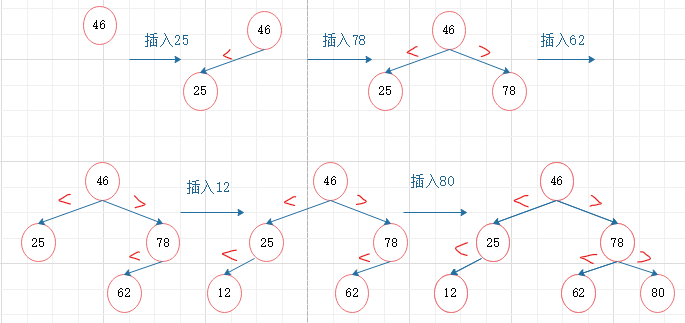
①插入
在二叉排序树中插入关键字为X的新结点:
(1)若二叉排序树BST为空,则新申请一个key为X的结点,作为根结点
(2)不为空,将X和根结点的key比较:
若X == BST->key,则说明树中已有此关键字k,无须插入
若X<BST->key,则将k插入左子树中
若X>BST->key,则将k插入右子树中
BinTree Insert(BinTree BST, ElementType X)
{
if (BST == NULL)
{
BST = (BinTree)malloc(sizeof(struct TNode));
BST->Data = X;
BST->Left = NULL;
BST->Right = NULL;
return BST;
}
else
{
if (X > BST->Data)
{
BST->Right = Insert(BST->Right, X);
}
else if (X < BST->Data)
{
BST->Left = Insert(BST->Left, X);
}
}
return BST;
}
②删除
(1)删除叶子结点:直接删除
(2)删除只有左子树或只有右子树的结点:用该结点的左子树或右子树代替它
(3)删除既有左子树,又有右子树的结点:用该结点的前驱(左子树的最大结点)或后继(右子树的最小结点)
BinTree Delete(BinTree BST, ElementType X)
{
if (BST == NULL)
{
printf("Not Found\n");
}
else
{
if (X > BST->Data)
{
BST->Right = Delete(BST->Right, X);
}
else if (X < BST->Data)
{
BST->Left = Delete(BST->Left, X);
}
else
{
if (BST->Left == NULL)//没有左子树
{
BST = BST->Right;
}
else if (BST->Right == NULL)//没有右子树
{
BST = BST->Left;
}
else//既有左子树又有右子树
{
BinTree q;
q = FindMin(BST->Right);//根节点右子树最小结点做根节点
BST->Data=q->Data;
BST->Right=Delete(BST->Right,BST->Data);
}
}
}
return BST;
}
③查找
按照二叉排序(查找)树特点:
若左子树不空,左子树上所有结点的值均小于根结点的值
若右子树不空,右子树上所有结点的值均大于根结点的值
所以:
X > BST->Data,左子树查找
X < BST->Data,右子树查找
BinTree Find(BinTree BST, ElementType X)
{
if (BST == NULL || BST->Data == X)//找到或找不到
{
return BST;
}
if (X > BST->Data)
{
return Find(BST->Right, X);
}
else if (X < BST->Data)
{
return Find(BST->Left, X);
}
}
查找ASL
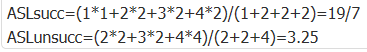
④找最小结点值(左子树最左结点)
BinTree FindMin(BinTree BST)
{
if (BST == NULL)
{
return BST;
}
while (BST->Left != NULL)//最左子树
BST = BST->Left;
return BST;
}
⑤找最大结点值(右子树最右结点)
BinTree FindMax(BinTree BST)
{
if (BST == NULL)
{
return BST;
}
while (BST->Right != NULL)//最右子树
BST = BST->Right;
return BST;
}
2、平衡二叉树(AVL树)
特点:
左、右子树也都是平衡二叉树
所有结点的左、右子树深度之差(平衡因子)的绝对值 ≤ 1
插入结点
①LL平衡旋转
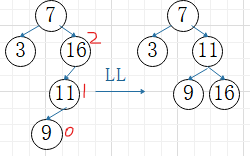
A结点的左子树的左子树上插入结点,使A结点平衡因子变为2,失衡需旋转
A的左孩子B向上旋转作为A的根结点
A结点向下旋转变为B的右孩子
B原来的右子树变为A的左子树
②RR平衡旋转
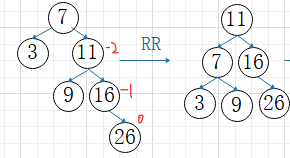
A结点的右子树的右子树上插入结点,使A的平衡因子变为-2,失衡需旋转
A的右孩子B向上旋转作为A的根结点
A结点向下旋转变为B的左孩子
B原来的左子树变为A的右子树
③LR平衡旋转
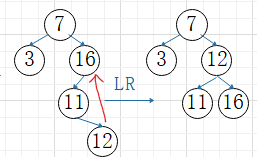
A的左子树的右子树上插入结点,使A的平衡因子变为2,(以插入的结点C为旋转轴),先C进行旋转,A再旋转
C向上旋转到A的位置,A作为C右孩子
C原左孩子作为B的右孩子
C原右孩子作为A的左孩子
④RL平衡旋转
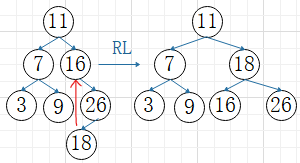
A的右子树的左子树上插入结点,使A的平衡因子从-1增加至-2,(以插入的结点C为旋转轴)
C向上旋转到A的位置,A作为C左孩子
C原左孩子作为A的右孩子
C原右孩子作为B的左孩子
调整原则:
了解是哪种失衡,谁是失衡点
如果有多个失衡点,从最下端的失衡点开始调整
每次调整后,检查是否二叉平衡树,是否还有失衡点存在
高度为h的需要最少结点数n的平衡二叉树
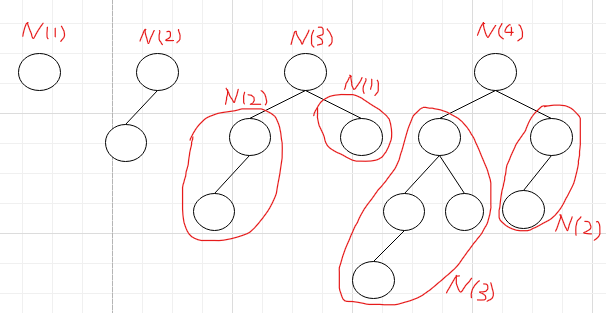
N(h)为Th的结点数
N(1)=1,N(2)=2,N(h)=N(h-1)+N(h-2)+1
3、B-树和B+树
BST和AVL树都是内存中,适用小数据量;每个节点放一个关键字,树的高度较大
而B-树和B+树(都是平衡树)可放外存,适合大数据量查找;一个节点可放多个关键字,降低树的高度
(1)B-树
一棵m阶B-树定义:
一棵空树或满足下列要求的m叉树:
根节点若不是叶子节点,根结点至少2个孩子节点
每个节点至多m个孩子节点(至多有m-1个关键字)
除根节点外,其他节点至少有【(m/2)取上限】个孩子节点(即至少有【(m/2)取上限-1】个关键字)
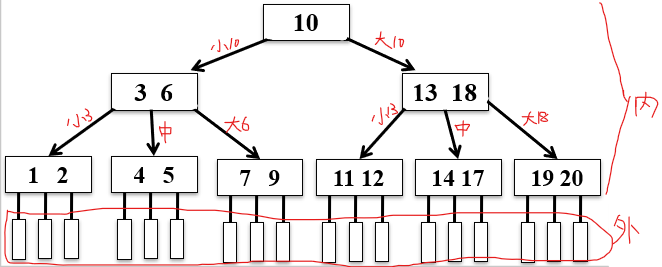
特点:
①若有结点(k0,ki,kn)
结点中按关键字大小顺序排列,ki<ki+1
pi为该节点的孩子指针:
p0 指向结点:关键字<k0
pi指向结点:关键字>=[ki,ki+1]
pn指向结点:关键字>kn
②B-树是所有结点的平衡因子均等于0的多路查找树
③所有外部结点都在同一层上
④在计算B-树的高度时,需要计入最底层的外部结点
⑤外部结点(失败结点)指向它的指针为空,不含有任何信息,是虚设的
一棵B树中若有n个关键字,则外部结点个数就为n+1
B-树操作
①B-树的查找
在一棵B-树上顺序查找关键字为X的方法为:
将X与根节点中的key[i]值进行比较
(1)若k=key[i],查找成功;落入一个外部结点,则查找失败
(2)若k<key[1]:则沿着指针ptr[0]所指的子树继续查找
(3)若key[i]<k<key[i+1]:则沿着指针ptr[i]所指的子树继续查找
(4)若k>key[n]:则沿着指针ptr[n]所指的子树继续查找
②B-树的插入:
在查找不成功之后,需进行插入;关键字插入的位置必定在叶子结点层:
该结点的关键字个数n<m-1,不修改指针
该结点的关键字个数 n=m-1,则需进行“结点分裂”
分裂过程
1.如果没有双亲结点,新建一个双亲结点,树的高度增加一层。
2.如果有双亲结点,将ki插入到双亲结点中。
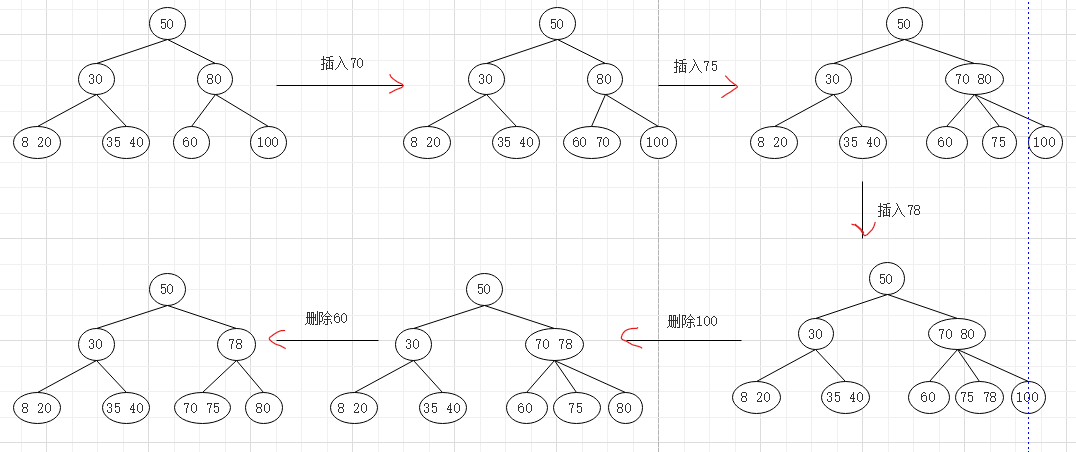
③B-树的删除:与插入相反
删除后的树必须满足:非根、非叶子结点的关键字最少个数Min=【(m/2)取上限-1】
(1)结点中关键字的个数>【(m/2)取上限-1】,直接删除
(2)结点中关键字的个数=【(m/2)取上限-1】,要从其左(或右)兄弟结点“借调”
(3)若其左和右兄弟结点均无关键字可借(结点中只有最少量的关键字),则必须进行结点的“合并”
1、B树非叶子节点删除
从该结点子树借调最大或最小关键字key代替该结点,并且在子树中删除key
若子树节点关键字个数<Min,需要进行结点的“合并”
2.B树叶子节点删除
该结点的关键字个数大于Min,说明删去该关键字后该结点仍满足B树的定义,则可直接删去该关键字
该结点的关键字个数等于Min,说明删去关键字后该结点将不满足B树的定义,若可以从兄弟结点借
兄弟结点最小关键字上移双亲结点
双亲结点大于删除关键字的关键字下移删除结点
该结点的关键字个数等Min,兄弟节点关键字个数也等于Min
兄弟节点及删除关键字节点、双亲结点中分割二者关键字合并一个新叶子结点
若双亲结点关键字个数<=Min再次分割
(2)B+树(大型索引文件的标准组织方式)
B+树的查找:
B+树查找效率高,同分块索引,多级索引结构
直接从最小关键字开始进行顺序查找所有叶节点链接成的线性链表
从B+树的根节点出发一直找到叶节点为止
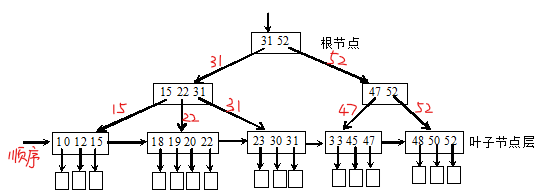
一棵m阶B+树特点:
(1)每个分支节点至多有m棵子树
(2)根节点或者没有子树,或者至少有两棵子树
(3)除根节点,其他每个分支节点至少有【(m/2)取上限】棵子树
(4)有n棵子树的结点有n个关键字
(5)所有子结点包含全部结点关键字及指向相应记录的指针(按关键字大小顺序链接)
(6)所有分支节点(可看成是分块索引的索引表)包含子结点最大关键字及指向子结点的指针
m阶的B+树和m阶的B-树不同点:
(1)非根结点关键字个数n不同、n取值范围不同
B+树中:一个节点n个孩子则对应n个关键字
取值范围:【(m/2)取上限】≤n≤m,根节点是1≤n≤m;
B-树中:一个节点n个孩子则对应n-1个关键字
取值范围:【(m/2)取上限-1】≤n≤m-1 ,根节点 1≤n≤m-1
根节点孩子至少为2
(2)叶子结点不一样
B+树所有叶子节点包含了全部关键字
B-树叶子节点包含的关键字与其他节点包含的关键字是不重复的
(3)B+树中所有非叶子节点仅起到索引的作用,而在B-树中,每个关键字对应一个记录的存储地址
(4)通常在B+树上有两个头指针,一个指向根节点,另一个指向关键字最小的叶子节点,所有叶子节点链接成一个不定长的线性链表
4、哈希(散列)查找
概念:
①哈希表(散列表)存储线性表的存储结构:主要适合关键字与存储地址存在某种函数关系的数据
②哈希函数h(key):把关键字为ki的对象存放在相应的哈希地址中
③哈希表:存储数据记录的长度为m(m≥n)的连续内存单元,线性表结构
④哈希冲突(同义词冲突):对于两个关键字分别为ki和kj(i≠j)的记录,有ki≠kj,但h(ki)=h(kj)
冲突(同义词冲突)有关因素:
①哈希表长度
②与装填因子有关
装填因子α=需要存储的数据个数/哈希表的大小
<span style="color:red">α越小,冲突可能性就越小;</span> α越大(最大可取1),冲突的可能性就越大;一般控制在0.6~0.9的范围内
③与所采用的哈希函数有关
④与解决冲突方法有关
哈希函数构造方法
1、直接定址法
直接定址法是以关键字k本身或关键字加上某个数值常量c作为哈希地址的方法
直接定址法的哈希函数h(k)为:h(k)=k+c
一般用于有连续规律的数据,例:h(学号)=学号-201601001
优点:计算简单,并且不可能有冲突发生
缺点:关键字分布不连续将造成内存单元的大量浪费
2. 除留余数法
除留余数法是用关键字k除以某个不大于哈希表长度m的数p所得的余数作为哈希地址的方法
哈希函数h(k)为:h(k)=k mod p (mod为求余运算,p≤m)
p最好是质数(素数):防止过多数据聚集在同一个地址
设某散列表的长度为100,散列函数H(k)=k % P,则P通常情况下最好选择97

哈希冲突解决方法
1、开放定址法:冲突时找一个新的空闲的哈希地址
结构体
typedef struct
{
int key;// 关键字域
InfoType data;//其他数据域
int count; //探查次数
}HashTable[MaxSize];
(1)线性探查法:di=(di-1+1) mod m (1≤i≤m-1)
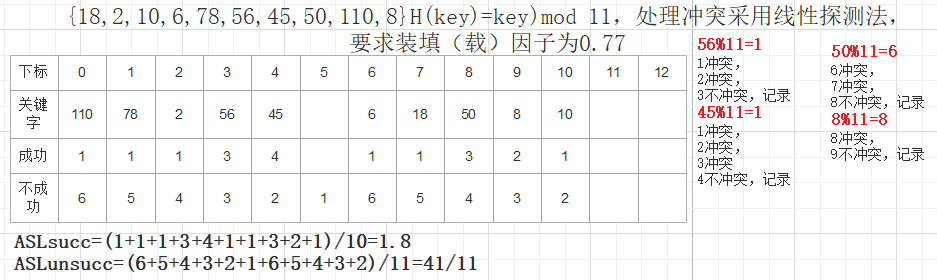
adr = k % p;
if (ha[adr].key == -1)
{
ha[adr].key = k;
ha[adr].count = 1;
}
else//地址已被占
{
i = 1;
while (ha[adr].key != -1)//向后查找空闲地址
{
if (ha[adr].key == k)
break;
adr = (adr + 1) % p;
i++;
}
ha[adr].key = k;
ha[adr].count = i;
}
缺点:非同义词冲突(哈希函数值不相同的两个记录争夺同一个后继哈希地址堆积(或聚集)现象)
(2)平方探查法: di=(d0±i2) mod m (1≤i≤m-1)
探测顺序:d0、d0 +1、d0 -1 、d0 +4、d0 -4
平方探查法是一种较好的处理冲突的方法,可以避免出现堆积现象
缺点:不能探查到哈希表上的所有单元,但至少能探查到一半单元
2、拉链法
(把所有的同义词用单链表链接起来)
结构体
typedef struct HashNode
{
int key;
struct HashNode *next;
}HashNode,* HashTable;
HashTable ht[MAX];
adr=k % p
ptr = ha[adr].first;
while (ptr != NULL)
{
if (ptr->user.ID == user.ID)//已有记录
break;
ptr = ptr->next;
}
if (ptr == NULL)//没有记录,头插法添加
{
ptr = new HTNode;
ptr->user = user;
ptr->next = ha[adr].first;
ha[adr].first = ptr;
}
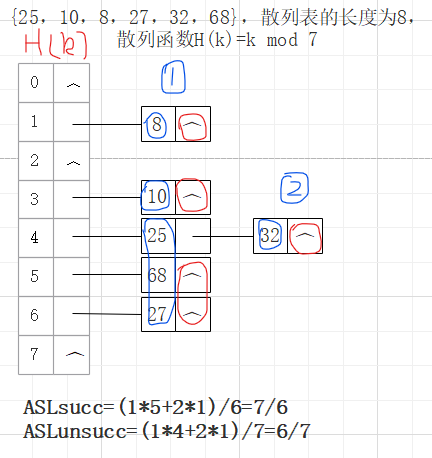
无堆积现象,链表法,空间利用率较高,不会过多浪费内存
1.2.谈谈你对查找的认识及学习体会
虽然查找的内容,大部分都多少有接触一点,但是学习过程中,还是有很多抽象的不理解的地方,比如B-树的插入删除,平衡树的调整,ASL的计算等等。让我学习到了如何更高效地实行查找
注意点:
①B-树的借位需要先判断,父亲结点或兄弟结点是否小于Min,不能随便借位
②平衡二叉树的调整,要遵循调整规则,若有多个需要调整的点,从最下方的失衡点开始调整
③B-树不能进行顺序查找,而B+树可以
④哈希表和哈希链,使用之前要进行初始化,哈希链插入结点前要先申请空间
⑤哈希表计算ASLunsucc时:
分母,使用的是求余的数p,而不是数据个数;
若倒数几个地址都为空,不能算入查找不成功的次数
2.PTA题目介绍
2.1 7-1 是否完全二叉搜索树
2.1.1 该题的设计思路
①二叉搜索树的建立:题目要求左子树键值大,右子树小,所以建立二叉搜索树的时候,插入结点比当前结点小的话进入右子树比较,否则进入左子树比较;要注意审题,并不是所有的二叉搜索树都是左小右大
②完全二叉树:非叶子结点层全满,最后一层结点不能有右无左
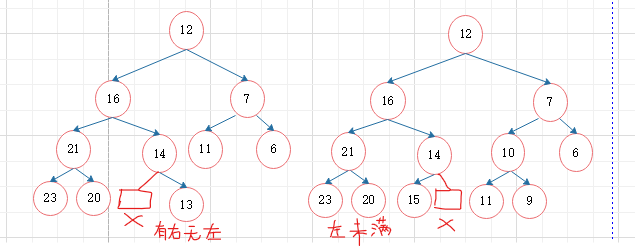
③每个结点都只遍历一次
时间复杂度为:O(n)
2.1.2 该题的伪代码
层次遍历(队列)
定义队列queue<BSTree>qu
入队根节点qu.push(BST)
while (队列不为空)
出队队头结点,若队头结点有左右子树,入队
若存在某结点没有左结点,但有右结点,说明不是完全二叉搜索树,则judge = false
遍历完一层结点后
if (height < (deep - 1))层数为倒数第二层之上
若非叶子结点没有全满pow(2, height),则judge = false;
若为最后一层叶子结点
若左子树叶子结点没全满的情况下,右子树有叶子结点,则judge = false;




2.1.3 PTA提交列表

①建树错误:
没注意是左子树键值大,右子树键值小
②未正确判断小于(deep - 1)层全满:
全满条件2(height-1)
③没考虑到倒数第二层存在有右子树无左子树的的情况:
设置变量flag=0(遍历每个结点之前都要初始化),若有左子树flag=1;若有右子树且flag=0,说明非完全;
④没考虑到左子树叶子结点未满,右子树有叶子结点的情况:
设置变量count记录每层总结点个数;设置变量lastCount记录符合完全树的结点(不存在右孩子时停止记录);若一层遍历结束count==lastCount说明是完全树
2.1.4 本题设计的知识点
1、层次遍历:应用队列,按照层次遍历整棵树
2、是否时完全二叉搜索树的条件:
叶子结点之上,为满二叉树;
叶子结点层:
(1)若左子树叶子结点未满,则右子树不能有叶子结点
(2)倒数第二层的结点若没有左孩子,一定没有右孩子
3、注意建树条件:左大右小还是左小右大
2.2 7-4 整型关键字的散列映射(2分)
①哈希表线性探查法解决冲突:
发生冲突的地址d0开始,依次探测d0的下一个地址(当到达哈希表表尾时,下一个探测地址为表首地址0),直到找到一个空闲的位置单元为止;若出现重复关键字的情况,不再次插入
例:

②初值设置
ha[i].key = -1;判断条件if (ha[adr].key == -1)
ha[i].count = 0;若不冲突,则count=1;若发生冲突,count=冲突次数+1
2.2.2 该题的伪代码
结构体
typedef struct node
{
int key; //关键字域
int data; //其他数据域
int count; //探查次数域
} HashTable[MaxSize]; //哈希表类型
定义哈希表HashTable ha
输入数据个数count,和哈希表长度p
输入数据存储在num[MaxSize]中
for i = 0 to p do
初始化哈希表
end for
for i = 0 to count do
插入数据到哈希表中
除留余数法求出对应地址adr = 数据 % 哈希表长度;
if (该地址没有数据)
数据加入该地址ha[adr].key = 数据,记录查找次数为1
else地址已被占
while (向后查找到一个没有数据的地址)
if (该数据已经有记录)退出循环
依次向后查找adr = (adr + 1) % p,并记录查找次数
数据加入该地址ha[adr].key = 数据,记录查找次数
end for


2.2.3 PTA提交列表

①超时,找不到符合条件地址:
没有正确初始化哈希表,查找次数和初值都要初始化
②没考虑重复关键字的情况:
解决冲突遍历向后查找中,若遇到相同关键字ha[adr].key==待加入数据,直接退出循环
③最大哈希表长度选取错误:
要找质数MaxSize应该是1007,而非1005
2.2.4 本题设计的知识点
哈希表线性探查法解决冲突:
①判断好求余的质数
②发生冲突的地址d0开始,依次探测d0的下一个地址(当到达哈希表表尾时,下一个探测地址为表首地址0),直到找到一个空闲的位置单元为止;若出现重复关键字的情况,不再次插入
2.3 7-5(哈希链) 航空公司VIP客户查询
①身份证前几位一般代表地区容易重复使数据堆积,所以取身份证号后5位,作为地址adr = adr * 10 + user.ID[k] - '0',若最后一位为‘x’当成10计算
②拉链法解决冲突:
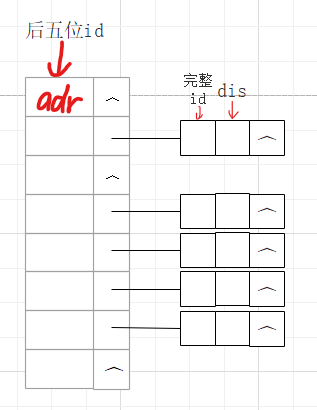
求余后同一个地址的元素,头插法,构成单链表
若已存在待插入的身份号,里程数增加,不重新开辟新的单元存储
2.3.2 该题的伪代码
结构体
typedef struct USER
{
string ID;//身份证号
int miles;//飞行里程数
}USER;//旅客信息
typedef struct Node
{
USER user;
struct Node* next;
}HTNode;
typedef struct
{
HTNode* first;
}HashTable;
初始化哈希链头结点
for i = 0 to MAX do
ha[i].first = NULL;
end for
for i = 0 to 添加记录数 do
输入身份信息和里程数,里程数小于最小里程的,按照最小里程计算
取身份证号后5位,作为地址adr = adr * 10 + user.ID[k] - '0'
遍历该地址为头结点的哈希链
if已有该用户信息
里程数叠加ptr->user.miles = ptr->user.miles + user.miles;
if没有记录,头插法添加
end for
for (i = 0; i < search; i++)
输入要查找的id
取身份证号后5位,作为地址adr = adr * 10 + user.ID[k] - '0'
遍历该地址为头结点的哈希链
if已有该用户信息,输出该用户总里程数
if没有记录,输出No Info
end for



2.3.3 PTA提交列表

①空间不足:
所有地址都要初始化,不能按照数据个数初始化
②大数据超时:
输入用scanf节省时间,要先申请string ID,ID.resize(字符串长度);
而用scanf输入string类型,要写成scanf(“%s”,&ID[0])字符串才能正确输入
③比较字符串大小错误:
string类型之间比较,不需要用到函数;若没有申请空间ID.resize(字符串长度),系统默认的可能比需要的小,导致字符串比较出错
2.3.4 本题设计的知识点
1、拉链法解决冲突:
数组和链表相结合
求余后同一个地址的元素,头插法,构成单链表
2、string类型,使用scanf输入更节省时间,但要先申请空间,不然数据较长时可能会读取出错





