DS博客作业04--图
0.PTA得分截图

1.本周学习总结
图(多对多)
逻辑结构描述:Graph = (V , E)
(1)有向图(边有方向)
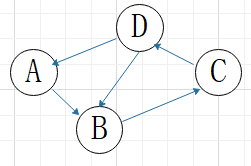
V1={A, B, C, D}
E1={<A,B>, <B,C>, <C,D>,<D,B>,<D,A>}
例:
顶点A的一条出边,同时也是顶点B的一条入边;顶点A和顶点B互为邻接点
度(以顶点i为终点的入边的数目为入度;以顶点i为始点的出边的数目为出度;度=入度+出度):
A出度为1,入度为1,度为2;B出度为1,入度为2,度为3;
(2)无向图(边没方向)
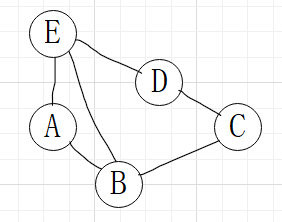
V2={A, B, C, D, E}
E2={(A,B), (A,E), (B,E),(D,E),(C,B),(C,D)}
例:
顶点A和顶点B互为邻接点
度(以顶点i为端点的边数):
A度为2;B度为3;C度为2
(3)完全图
①无向图:每两个顶点之间都存在着一条边,称为完全无向图,包含有n(n-1)/2条边

②有向图:每两个顶点之间都存在着方向相反的两条边,称为完全有向图,包含有n(n-1)条边

图接近完全图时,称为稠密图
相反,当一个图含有较少的边数(即当e<<n(n-1))称为稀疏图
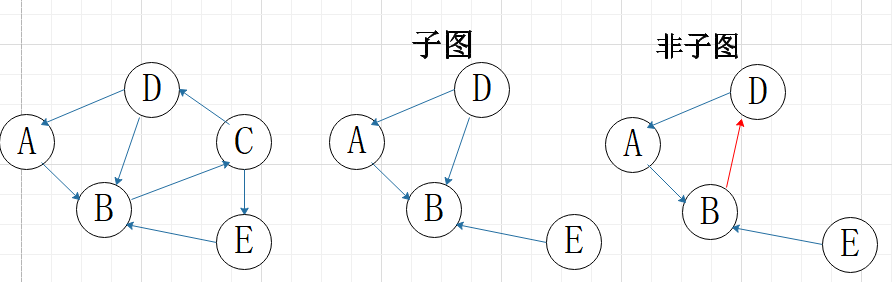
(4)子图
顶点和边(包括方向)都需是原图的子集
(5)路径
①路径长度:一条路径上经过的总边数
②简单路径:一条路径上除开始点和结束点可以相同(也可不相同),其余顶点均不相同
③回路或环:一条路径上的开始点与结束点为同一个顶点
④简单回路或简单环:开始点与结束点相同的简单路径
(6)连通
①无向图:
连通:若从顶点i到顶点j有路径
连通分量:无向图中的极大连通子图
连通图:若图中任意两个顶点都连通(有路径)[连通分量只有一个(本身)]

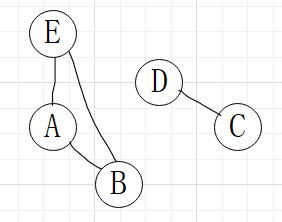
非连通图:存在若干个不相连接的连通图(有多个连通分量)
②有向图:
强连通图:任意两个顶点之间都存在一条有向路径

非强连通图:各个强连通子图称作它的强连通分量

③找强连通分量:
在图中找有向环
扩展:如果某个顶点到该环中任一顶点有路径,并且该环中任一顶点到这个顶点也有路径,则加入这个顶点
1.1.1图存储结构
例:

(1)邻接矩阵(二维数组)
①二维数组edges[MAXV][MAXV]表示各个顶点之间关系(一般以行为先)
②若顶点数很多的情况下,可以引用二级指针
int **edges;(每个点都需要动态申请内存)
结构体定义(注意结构体定义顺序)
#define MAXV <最大顶点个数>
typedef struct
{ int no; //顶点编号
InfoType info; //顶点信息
} VertexType;//顶点信息
typedef struct
{ int edges[MAXV][MAXV]; //邻接矩阵
int n; //边数
int e; //顶点数
VertexType vexs[MAXV]; //顶点信息
} MGraph;//图的定义

MGraph g;
for (i = 1; i <= n; i++)//初始化二维数组
for (j = 1; j <= n; j++)
g.edges[i][j] = 0;
for (i = 0; i < e; i++)//建立顶点之间联系
{
cin >> node1 >> node2;
g.edges[node1][node2] = 1;//无向图建立
g.edges[node2][node1] = 1;
//有向图只需g.edges[node1][node2] = 1;
}
存储空间为O(n2)
每个图的邻接矩阵表示是唯一的
适合稠密图的存储
(2)邻接表
(顺序表与链表相结合)
①对图中每个顶点建立一个单链表,将所有邻接点用链串起来
②每个单链表上添加一个表头结点储存顶点信息
③将所有表头结点构成一个数组
结构体定义(注意结构体定义顺序)
typedef struct ANode
{ int adjvex; //该边的终点编号
struct ANode *nextarc; //指向下一条边的指针
InfoType info; //该边的权值等信息
}ArcNode;//结点信息,定义在最前面(后面结构体有定义)
typedef struct Vnode
{ Vertex data;
ArcNode *firstarc; //指向每个顶点(表头)的第一条边
}VNode;//顶点信息
typedef struct
{ VNode adjlist[MAXV] ; //邻接表(表头数组)
int n; //图中顶点数n
int e; //图中边数e
}AdjGraph;//邻接表

AdjGraph*& G
ArcNode* ptr;
G = new AdjGraph;
for (i = 1; i <= n; i++)//初始化
{
G->adjlist[i].firstarc = NULL;
G->adjlist[i].data = i;
}
for (i = 0; i < e; i++)//建无向图
{
cin >> node1 >> node2;
ptr = new ArcNode;
ptr->adjvex = node2;
ptr->nextarc = G->adjlist[node1].firstarc;//采用头插法插入结点
G->adjlist[node1].firstarc = ptr;//若为无向图,只需单向建立,不需要后序步骤
ptr = new ArcNode;
ptr->adjvex = node1;
ptr->nextarc = G->adjlist[node2].firstarc;
G->adjlist[node2].firstarc = ptr;
}
存储空间为O(n+e)
适合稀疏图的存储
1.1.2图遍历连通
例:


(1)深度优先遍历(DFS)
(递归)
选择一个与当前顶点相邻且没被访问过的顶点为初始顶点u,再从u出发进行深度优先搜索,直到图中与当前顶点邻接的所有顶点都被访问过为止
Int visited[最大顶点数]
void DFS(ALGraph *G,int v)
{
ArcNode *ptr;
visited[v]=1; //标记已访问顶点
cout<<v;
ptr=G->adjlist[v].firstarc;
while (ptr!=NULL)
{
if (visited[ptr->adjvex]==0) //若未被访问过
DFS(G,ptr->adjvex); //递归
ptr=ptr->nextarc;
}
}
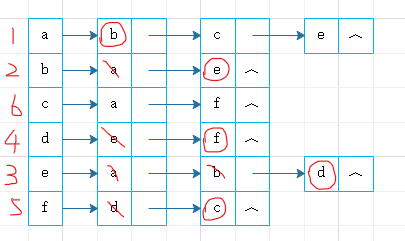
若图为非连通图(多次调用DFS)
for (v=0; v<G.vexnum; ++v)
if (!visited[v])
DFS(G,v); // 如果还有未访问的顶点再次调用DFS,直到所有顶点都访问过
(2)广度优先遍历(BFS)
(队列)
访问当前顶点的所有未被访问过的邻接点,按照先后次序访问每一个顶点的所有未被访问过的邻接点
void BFS(AdjGraph* G, int v) //v节点开始广度遍历
{
queue<int>qu;
ArcNode* p;
int front;//队头元素
int visited[MAX] = { 0 };//标记已遍历过的结点
visited[v] = 1;
qu.push(v);
while (!qu.empty())
{
front = qu.front();
qu.pop();
cout<<front;
p = G->adjlist[front].firstarc;
while (p)//遍历当前顶点的整条链
{
if (!visited[p->adjvex])
{
visited[p->adjvex] = 1;//标记已遍历过的结点
qu.push(p->adjvex);
}
p = p->nextarc;
}
}
}
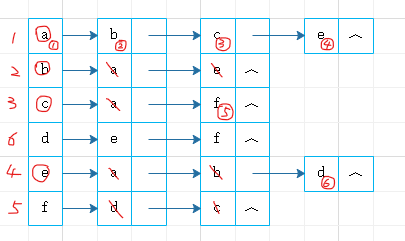
若图为非连通图(多次调用BFS)
for (v=0; v<G.vexnum; ++v)
if (!visited[v])
BFS(G,v); // 如果还有未访问的顶点再次调用BFS,直到所有顶点都访问过
1.1.3最小生成树
特点:
连接所有顶点,权值之和最小的生成树
含有图中全部n个顶点和构成一棵最小生成树有(n-1)条边(可用来判断图是否连通)
如果在一棵生成树上添加一条边,必定构成一个环
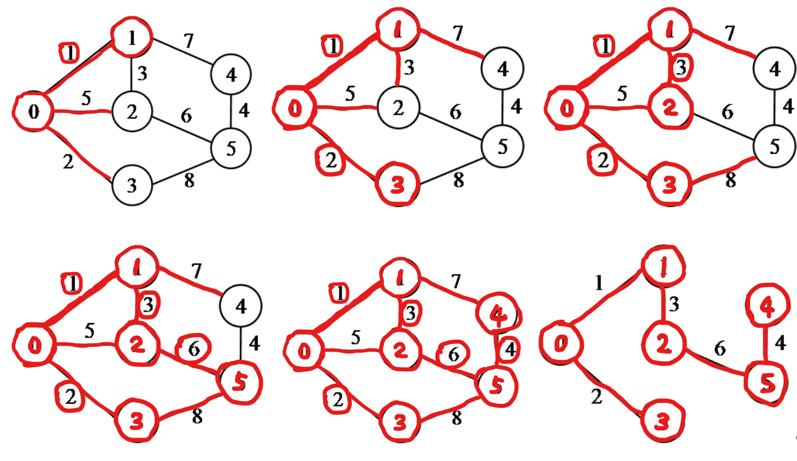
(1)普里姆Prim算法
初始化U={v},找到v到其他顶点的所有边为候选边
重复以下步骤n-1次,使其他n-1个顶点都加入到U中
在未加入集合U的顶点中找出离集合U中顶点最近的顶点k
在未加入集合U的顶点中若存在顶点j使得(j,k)的权值小于原来和顶点k关联的候选边,则用(k,j)取代后者作为候选边
1.closest[i]:最小生成树的边连接的在U中顶点编号
2.lowcost[i]:顶点i(i属于未加入顶点集U的顶点)到U中顶点的边权重,取最小权重的顶点k加入U
lowcost[k]=0表示这个顶点在U中
3.(closest[k],k)构造最小生成树一条边
void Prim(MGraph g,int v)
{
int lowcost[MAXV];
int min;
int closest[MAXV];
int i,j,k;
for (i=0;i<g.n;i++) //给lowcost[]和closest[]置初值
{
lowcost[i]=g.edges[v][i];
closest[i]=v;
}
for (i=1;i<g.n;i++) //将剩余(n-1)个顶点逐步添加进集合U
{
min=INF;
for (j=0;j<g.n;j++) //在未加入集合U的顶点中找出离集合U中顶点最近的顶点k
if (lowcost[j]!=0 && lowcost[j]<min)
{
min=lowcost[j];
k=j;//记录最近顶点的编号
}
printf("边(%d,%d);权为:%d\n",closest[k],k,min);
lowcost[k]=0; //标记k已经加入集合U
for (j=0;j<g.n;j++) //修改数组lowcost和closest的值
if (lowcost[j]!=0 && g.edges[k][j]<lowcost[j])
{
lowcost[j]=g.edges[k][j];
closest[j]=k;
}
}
}
贪心算法(不需要回溯)
只考虑当前最优,不从整体最优上考虑,形成的是局部最优解(并不保证得到全局最优解)
把一个问题分成若干个子问题
解决每一子问题,得到子问题的局部最优解
把子问题局部最优解合成,就是问题的一个解
优点:时间空间复杂度小,效率高
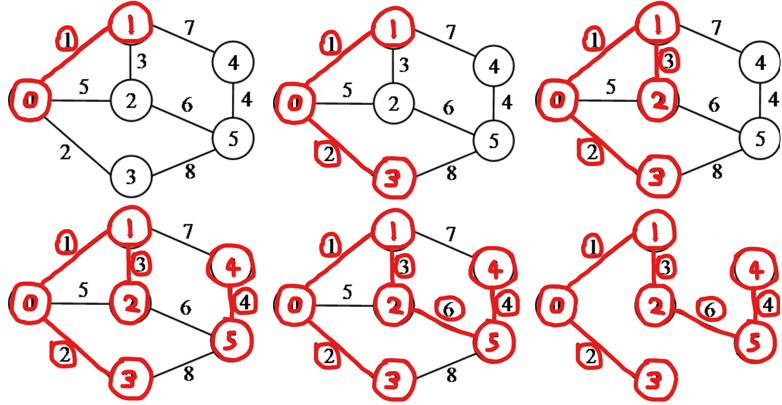
(2)克鲁斯卡尔(Kruskal)算法过程:
typedef struct
{ int u; //边的起始顶点
int v; //边的终止顶点
int w; //边的权值
} Edge;
for (i = 1; i <= G->n; i++)//遍历邻接表,将表中顶点之间联系存入结构体数组 E 中
{
p = G->adjlist[i].firstarc;
while (p != NULL)
{
E[k].start = i;
E[k].end = p->adjvex;
E[k].weight = p->weight;
k++;
p = p->next;
}
}
可以使用并查集,也可以使用数组(值相同表示相同集合)
sort(E, E + G->e, cmp); /*bool cmp(Edge a, Edge b)
//按权值大小升序排序 {
return a.weight < b.weight;//权值比较
}*/
for (i = 1; i <= G->n; i++)//集合初始化
vset[i] = i;
j = 0;
while (j < k - 1)//遍历完所有边
{
u = E[j].start;//起点
v = E[j].end;//终点
sn1 = vset[u];
sn2 = vset[v];
if (sn1 != sn2)//两顶点不属于同集合,不形成回路
{
cout<<u<<v;
for (i = 1; i <= G->n; i++)//将已连接的边并入同个集合
if (vset[i] == sn2)
vset[i] = sn1;
}
j++;//下一条边
}
1.1.4最短路径

(1)狄克斯特拉Dijkstra算法
数组dist[]:记录源点V到每个顶点的最短路径长度:初值或无路径用INF(无穷)表示
数组path[]:最短路径序列的前一顶点的序号;初值或无路径用-1表示
数组s[]:表示最短路径顶点集合(记录已加入顶点集的顶点)

void Dijkstra(int start, int end, int city)
{
Node dist[MAX];//路径数据
int s[MAX] = { 0 };//标记已走过结点
Node mindis;
for (i = 0; i < city; i++)//dist数组初始化
{
dist[i].distance = edges[start][i].distance;
dist[i].cost = edges[start][i].cost;
}
s[start] = 1;//标记起始点已走过
for (i = 0; i < city; i++)
{
mindis.distance = INF;
for (j = 0; j < city; j++)
if (s[j] == 0 && dist[j].distance < mindis.distance)//找距离最短的点
{
k = j;
mindis.distance = dist[j].distance;
mindis.cost = dist[j].cost;
}
s[k] = 1;//标记已走
for (j = 0; j < city; j++)
if (s[j] == 0)
if(edges[k][j].distance < INF)//连通
if (dist[k].distance + edges[k][j].distance < dist[j].distance)//过k点到j点的新路径比原来短,更新路径长度和价格
{
dist[j].distance = dist[k].distance + edges[k][j].distance;
dist[j].cost = dist[k].cost + edges[k][j].cost;
}
}
(2)弗洛伊德Floyd算法
二维数组表示dist,path


行->列最短路径长度:方位值
行->列最短路径:逆序
void Floyd(MatGraph g) //求每对顶点之间的最短路径
{
int A[MAXVEX][MAXVEX]; //建立A数组
int path[MAXVEX][MAXVEX]; //建立path数组
int i, j, k;
for (i = 0; i < g.n; i++)
for (j = 0; j < g.n; j++)
{
A[i][j] = g.edges[i][j];
if (i != j && g.edges[i][j] < INF)
path[i][j] = i; //i和j顶点之间有一条边时
else //i和j顶点之间没有一条边时
path[i][j] = -1;
}
for (k = 0; k < g.n; k++) //求Ak[i][j]
{
for (i = 0; i < g.n; i++)
for (j = 0; j < g.n; j++)
if (A[i][j] > A[i][k] + A[k][j]) //找到更短路径
{
A[i][j] = A[i][k] + A[k][j]; //修改路径长度
path[i][j] = k; //修改经过顶点k
}
}
}
1.1.5拓扑排序
(有回路,无法拓扑排序,所以拓扑排序可以用来检测图中是否有回路)
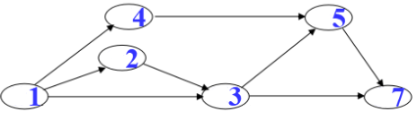
选取一个没有前驱的顶点,输出
从有向图中删去此顶点以及所有它的出度(并不是在图结构上真实删除)
重复上述两步,直至图空,或者图不空但找不到无前驱的顶点为止
该图拓扑排序:两种
1-2-4-3-5-7
1-4-2-3-5-7
for (i = 0; i < G->n; i++)
G->adjlist[i].count = 0;//所有顶点入度初始化为0
for (i = 0; i < G->n; i++)
{
ptr = G->adjlist[i].firstarc;
while (ptr != NULL)//求所有顶点的入度
{
G->adjlist[ptr->adjvex].count++;
ptr = ptr->nextarc;
}
}
for (i = 0; i < G->n; i++)
{
if (G->adjlist[i].count == 0)//入度为0结点进栈
{
top++;
St[top] = i;
}
}
while (top > -1)//栈不为空
{
i = St[top];
top--;
print[k++] = i;
ptr = G->adjlist[i].firstarc;
while (ptr != NULL)
{
G->adjlist[ptr->adjvex].count--;//除去与已输出顶点之间联系(并不是真的删除)
if (G->adjlist[ptr->adjvex].count == 0)//入度为0结点进栈
{
top++;
St[top] = ptr->adjvex;
}
ptr = ptr->nextarc;
}
}
if (k != G->n)//判断是否有回路
{
cout << "error!";
}
1.1.6关键路径(最长路径)
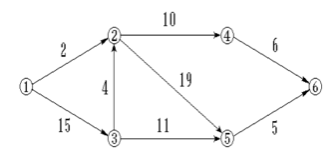
ve(v):v作为源点事件最早开始时间为0
①ve(v) = Max{ve(x) + 所有相邻顶点边的权值比较}
vl(v):定义在不影响整个工程进度的前提下,事件v必须发生的时间称为v的最迟开始时间
①vl(v)=ve(v) 当v为终点时
②vl(v)=MIN{vl(x)-所有相邻顶点边的权值} 其他顶点
活动a(边)的最早开始时间e(a)指该活动起点x事件的最早开始时间:e(a)=ve(x)
活动a(边)的最迟开始时间l(a)指该活动终点y事件的最迟开始时间与该活动所需时间之差:l(a)=vl(y)-time
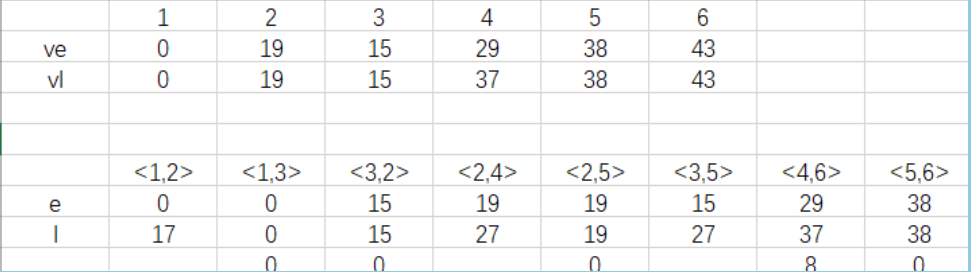
工程最早可能结束时间:43天
关键活动:1-3-2-5-6
1.2.谈谈你对图的认识及学习体会。
图的结构和关系跟之前学的相比更复杂,应用也很多,有些看了一遍再用,比如最小生成树和最短距离解法会混淆,通过再次复习,更深刻了一点,但是还有些没理解的地方(特别是关键路径)。画图辅助还是很重要!
>注意点:</span
①初始化(邻接表头节点,visited数组,边之间联系等等)和动态申请空间(建邻接表循环内都要新结点都要记得申请内存)
②正确判断是使用邻接矩阵还是邻接表,邻接矩阵内存不够可以改为二级指针(动态申请内存)
③迭代法和递归设置正确出口
④判断图是有向图操作还是无向图,是否连通
2.阅读代码
2.1 找到小镇的法官



2.1.1 该题的设计思路
信任别人是出度,被人信任是入度,找入度为N-1的人

2.1.2 该题的伪代码
定义int* ret_val = (int*)calloc(N + 1, sizeof(int))并初始化
记录每个人被相信的次数(入度)
++ret_val[trust[i][0]]
如果某个人相信了别人(出度不为0),说明他不是小镇法官,把被相信的次数清零
ret_val[trust[i][0]] = 0
查找被相信次数为N-1的人(入度为N-1的人)
如果有大于1个的法官,说明无法确认身份,否则就为该下标
2.1.3 运行结果

2.1.4分析该题目解题优势及难点
优点:利用图结构很好解决了信任和被信任问题,把题目的逻辑关系清楚表达
难点:数组结构的利用,信任和被信任关系解除很巧妙
2.2 跳跃游戏 II


2.1.1 该题的设计思路
当一次跳跃结束时,从下一个格子开始,到现在能跳到最远的距离,都是下一次跳跃的起跳点

2.2.2 该题的伪代码
while(在跳跃范围内)
for i = start to end do
求出能跳到最远的距离 maxPos = max(maxPos, i + nums[i])
end for
更新下一次起跳点范围开始的格子
更新下一次起跳点范围结束的格子
每完成一次跳跃记录跳跃次数
2.2.3 运行结果
2.2.4分析该题目解题优势及难点
优点:利用动态规划和贪心算法,只关心怎么去跳不关心跳几次,可以更快得到最小跳跃次数,从局部最优最后化为整体最优
难点:思路直接看有点难理解后面看了评论解析结合图,才看懂
2.3 不邻接植花



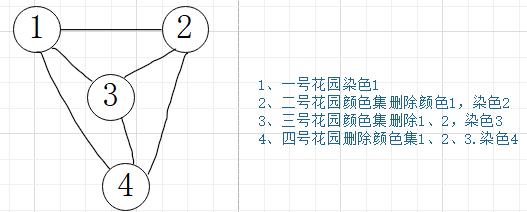
2.3.1 该题的设计思路
1、根据paths建立邻接表
2、默认所有的花园先不染色
3、从第一个花园开始走,把与它邻接的花园的颜色从color颜色集中删除
4、删除所有与它相邻的颜色,在集合中剩下的颜色就可以随机选择
5、循环第3和4步直到最后一个花园染色完
2.3.2 该题的伪代码
利用vector<int> G[N],并根据paths建立邻接表
for i = 0 to paths.size() do建立无向图
G[paths[i][0] - 1].push_back(paths[i][1] - 1);
G[paths[i][1] - 1].push_back(paths[i][0] - 1);
end for
vector<int> answer(N, 0)所有的花园先不染色
for i = 0 to N do
定义set<int>color{ 1,2,3,4 }保存染色集合
for j = 0 to G[i].size() do
把已染过色从color集合中的去除color.erase()
end for
将集合中当前的第一个颜色赋给当前花园answer[i]=*(color.begin())
end for
2.3.3 运行结果

2.3.4分析该题目解题优势及难点
优点:使用邻接矩阵的话会堆栈溢出,改为邻接表法,邻接表的建立跟学的不同用vector连接当链;利用set集合去除相邻已染过的颜色,使得不会重复
难点:化为图结构做就相对比较简单





