完全背包基础详解(附求解选择的物品)

资料摘自背包九讲 and http://blog.csdn.net/wumuzi520/article/details/7014830 and http://www.wutianqi.com/?p=539

首先说明一下什么是完全背包

有N种物品和一个容量为V的背包，每种物品都有无限件可用。第i种物品的费用是c[i]，价值是w[i]。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量，且价值总和最大。这个问题其实和01背包很像，只不过每种物品都有无限件。即每一种决策不只有一种状态，可以选0件，选1件.....

根据01背包的思想我们可以得出这样的伪代码：

<span style="font-family:Microsoft YaHei;font-size:14px;">     F[0][] ← {0}

     F[][0] ← {0}

     for i←1 to N

         do for j←1 to V

             do for k←0 to j/C[i]

                if(j >= k*C[i])

                     then F[i][k] ← max(F[i][k],F[i-1][j-k*C[i]]+k*W[i])

     return F[N][V]
</span>

 简单优化

        若两件物品满足C[i] ≤C[j]&&W[i] ≥W[j]时将第j种物品直接筛选掉。因为第i种物品比第j种物品物美价廉，用i替换j得到至少不会更差的方案。

       这个筛选过程如下：先找出体积大于背包的物品直接筛掉一部分（也可能一种都筛不掉）复杂度O(N)。利用计数排序思想对剩下的物品体积进行排序，同时筛选出同体积且价值最大的物品留下，其余的都筛掉（这也可能一件都筛不掉）复杂度O(V)。整个过程时间复杂度为O(N+V)

（以上内容来自背包九讲）

利用01背包的思想转换

思考，01背包中每种物品只有一件，取或者不取。完全背包则每件物品都有无数件，那么可以取很多件。

那么对于第i种物品的出现，我们对第i种物品放不放入背包进行决策。如果不放那么F[i][j]=F[i-1][j]；如果确定放，背包中应该出现至少一件第i种物品，所以F[i][j]种至少应该出现一件第i种物品,即F[i][j]=F[i][j-C[i]]+W[i]。为什么会是F[i][j-C[i]]+W[i]？因为F[i][j-C[i]]里面可能有第i种物品，也可能没有第i种物品。我们要确保F[i][j]至少有一件第i件物品，所以要预留C[i]的空间来存放一件第i种物品。

那么状态方程为：

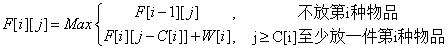
代码如下:

<span style="font-family:Microsoft YaHei;font-size:14px;">for(int i = 0 ; i < N ; i ++)
{
	for(int j = c[i] ; j <= V ; j++)
		f[i][j] = max(f[i-1][j],f[i][j-c[i]]+w[i]);
		
}</span>

优化,用一个一维数组来存储状态：

先给出状态方程和代码之后进行解释......

状态方程：

代码：

<span style="font-family:Microsoft YaHei;font-size:14px;">for(int i = 0 ; i < N ; i ++)
{
	for(int j = c[i] ; j <= V ; j++)
		f[j] = max(f[j],f[j-c[i]]+w[i]);
		
}</span>

......没想到竟然和01背包的差不多...差别只在j的遍历顺序上，这里是顺序遍历（01背包是逆序）

01背包中逆序是因为F[i][]只和F[i-1][]有关，且第i件的物品加入不会对F[i-1][]状态造成影响。而完全背包则考虑的是第i种物品的出现的问题，第i种物品一旦出现它势必应该对第i种物品还没出现的各状态造成影响。也就是说，原来没有第i种物品的情况下可能有一个最优解，现在第i种物品出现了，而它的加入有可能得到更优解，所以之前的状态需要进行改变，故需要正序。

选择物品的打印：

背包中放入哪些物品的求法和01背包情况差不多，从F[N][V]逆着走向F[0][0]，设i=N,j=V，如果F[i][j]==F[i][j-C[i]]+W[i]说明包里面有第i件物品，同时j -= C[i]。完全背包问题在处理i自减和01背包不同，01背包是不管F[i][j]与F[i-1][j-C[i]]+W[i]相不相等i都要减1，因为01背包的第i件物品要么放要么不放，不管放还是不放其已经遍历过了，需要继续往下遍历而完全背包只有当F[i][j]与F[i-1][j]相等时i才自减1。因为F[i][j]=F[i-1][j]说明背包里面不会含有i，也就是说对于前i种物品容量为j的背包全部都放入前i-1种物品才能实现价值最大化，或者直白的理解为前i种物品中第i种物品物不美价不廉，直接被筛选掉。

当然如果只用一维数组来存储状态的话是用上边的判断方法是不可以的，应当加入一个path[i][j]

处理时代码如下：

<span style="font-family:Microsoft YaHei;font-size:14px;">for(int i = 0; i < N; i++)  
{  
    for(int j = c[i]; j <=V; j++)  
    {  
        if(f[j] < f[j-c[i]]+w[i])  
        {  
            f[j] = f[j-c[i]]+w[i];  
            Path[i+1][j] = 1;  
        }  
    }     
}  </span>

输出时代码如下：

<span style="font-family:Microsoft YaHei;font-size:14px;">int i = N, j = V;  
while(i > 0 && j > 0)  
{  
    if(Path[i][j] == 1)  
    {  
        cout << c[i-1] << " ";  
        j -= c[i-1];  
    }  
    else  
        i--;  
}  </span>

动态规划的问题不好想明白.....明确理解动态规划方程的含义非常有必要。也是进步的一大要素吧。