10.16闲话：abc + 2 > a + b + c 的几何证法

来自wxy大佬的一道题

已知 \(|a|,|b|,|c|<1\)，求证： \(abc + 2 > a + b + c\)。

这里给出几何方法：

设 \(a,b,c\) 的绝对值分别为 \(x, y, z\)

考虑构造如下图形：

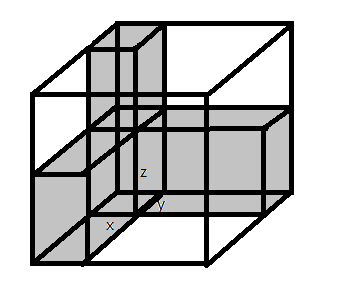
\(x,y,z\) 为图中标示的对应边，而外面的立方体棱长为 1 。
显然有灰色图形体积小于立方体体积，即 \(1>(xy+xz+yz)-2xyz\)

再有如下图形：

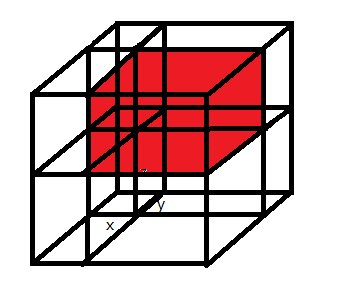
显然有白色部分体积（除去一角的红色立方体剩余的部分）小于立方体体积，即 \(1 > (x +y + z) - (xy + xz + yz) + xyz\)

两式相加得， \(2>(x+y+z)-xyz\)

设 \(a, b, c\) 从小到大排序为 \(p_1, p_2,p_3\)

• 当全为正时， \((x + y + z) - xyz = (a + b + c) - abc\)

• 当有一个为负时, \((x + y + z)-xyz - (p_1+p_2+p_3) + p_1p_2p_3 = 2p_1 - 2p_1p_2p_3 = 2p_1(1 - p_2p_3) < 0\) ， \(\therefore (x+y+z)-xyz > (a+b+c)-abc\)

• 当有两个为负时，\((x+y+z) - xyz -(p_1+p_2+p_3)+p_1p_2p_3 = 2p_1+2p_2-z(xy+p_1p_2) < 0\)， \(\therefore (x+y+z)-xyz > (a+b+c)-abc\)

• 当三个为负时，\((x+y+z) - xyz -(p_1+p_2+p_3)+p_1p_2p_3 < 0\)

综上： \((a+b+c)-abc\le (x+y+z)-xyz < 2\)
\(\therefore 2 + abc > a+b+c\)