9.29闲话:9.24数学周练(第二次)拓展
关于这张卷子呢,其实还是有点东西的,但是cxc上课讲的过于答辩,在这里写些题目的拓展解法和结论。
T7(单选倒数第二题)
题面
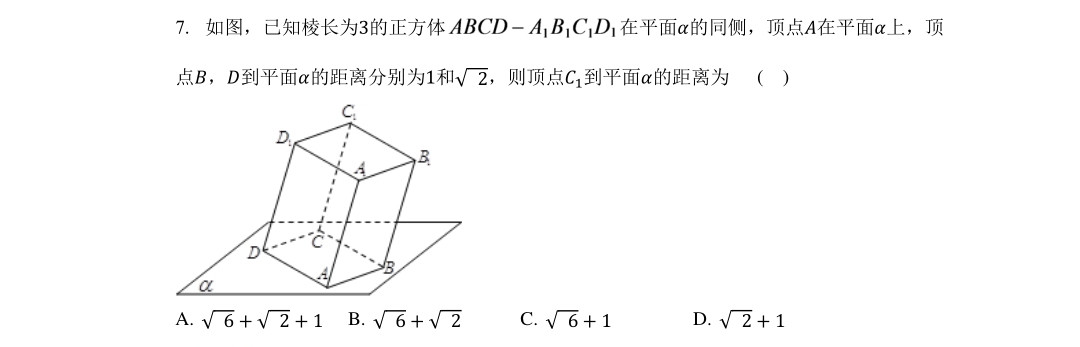
解法
求\(C_1\) 到平面 \(\alpha\) 的距离,其实也就是求 \(\overrightarrow{AC_1}\) 在平面 \(\alpha\) 的法向量的投影的模长。
而\(\overrightarrow{AC_1} = \overrightarrow{AA_1} + \overrightarrow{AB} + \overrightarrow{AD}\),那么 \(\overrightarrow{AC_1}\) 在平面 \(\alpha\) 法向量上模长等于分解的三个向量在法向量上投影之和的模长。
其中,\(\overrightarrow{AB}\) 和 \(\overrightarrow{AD}\) 的投影模长都已知道,问题是求 \(\overrightarrow{AA_1}\) 的投影模长。
这个选项出的太傻逼了点,因为我们知道其中肯定含有两已知向量投影模长,那么答案中大概率会有 \(\sqrt{2} + 1\), 这样就基本可以确定选 \(A\) 了, 如果是我出这题,可能我会把这题选项出成:
\(A.2\sqrt{2} + 1 \qquad B.\sqrt{3} + \sqrt{2}+1 \qquad C.\sqrt{5}+\sqrt{2}+1\qquad D.\sqrt{6}+\sqrt{2}+1\)
我们再回来看如何求 \(A_1\) 到平面 \(\alpha\) 的距离,这里其实存在如下结论:
空间中任意两两垂直且不重合的三条线段所在直线与任意平面所成线面角的正弦值的平方和为一
即有如下式子:\(\sum \sin^2\alpha = 1\) ,考虑怎么证明这个结论。
取三条线段同向的三个单位向量 \(\vec{a}\),\(\vec{b}\),\(\vec{c}\),设平面法向量为 \(\vec{n}\) 。
证明该结论,也就是证明这三个向量与法向量余弦的平方和为 1 ,即证:
\((\frac{|\vec{a}\ \cdot\ \vec{n} |}{|\vec{a} |\times |\vec{n}|})^2 + (\frac{|\vec{b}\ \cdot\ \vec{n} |}{|\vec{b} |\times |\vec{n}|})^2 +(\frac{|\vec{c}\ \cdot\ \vec{n} |}{|\vec{c} |\times |\vec{n}|})^2 = 1\)
设 \(\vec{n} = x\vec{a} + y\vec{b} + z\vec{c}\) ,因为基底都为单位向量,则
\(\begin{aligned}
(\frac{|\vec{a}\ \cdot \ \vec{n} |}{|\vec{a} |\times |\vec{n} |})^2+(\frac{|\vec{b}\ \cdot\ \vec{n} |}{|\vec{b} |\times |\vec{n} |})^2+(\frac{|\vec{c}\ \cdot\ \vec{n} |}{|\vec{c} |\times |\vec{n} |})^2 & = (\frac{x}{|\vec{n}|} )^2+(\frac{y}{|\vec{n}|} )^2+(\frac{z}{|\vec{n}|} )^2 \\ & = \frac{x ^ 2 + y ^ 2 + z ^ 2}{\vec{n}^2 } \\ & = 1 \end{aligned}\)
证毕。
现在我们把这个结论用到题目中,显然有
\((\frac{1}{3})^2 + (\frac{\sqrt{2} }{3})^2 +(\frac{x}{3})^2 = 1\)
其中 \(x\) 即为 \(A_1\) 到平面 \(\alpha\) 的高,解得\(x=\sqrt{6}\) 。
其实还可以发现有意思的一点,这个结论在在平面几何也是成立的也就是
平面中任意两个垂直线段所在的直线与平面中任意一条直线所成角的余弦值的平方和为一
也就是下图中的\(\sin^2\alpha + \sin^2\beta = 1\)
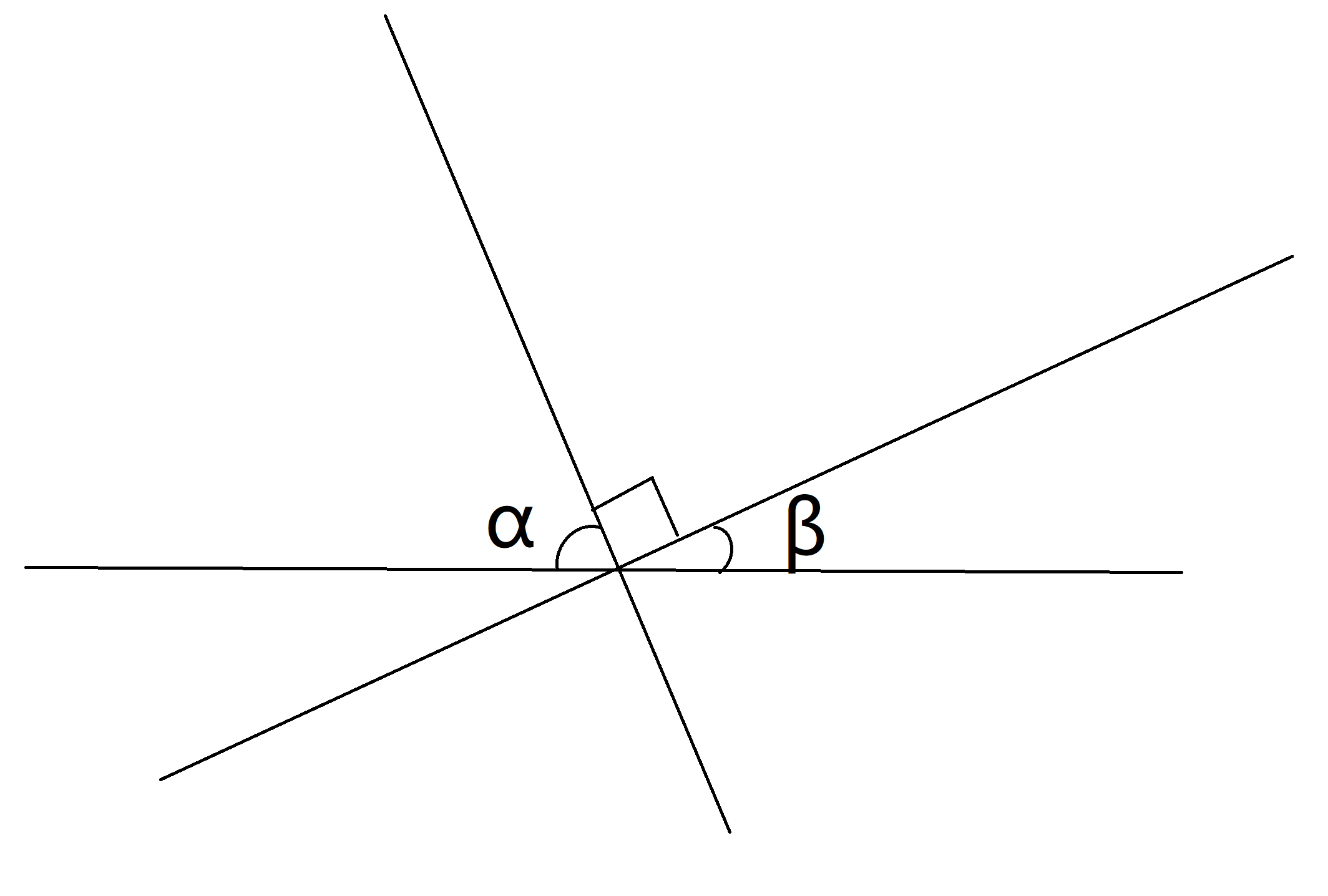
证明比较容易,这里不给出了。
T16(填空最后一题)
题面

解法
在利用拓展方法解决该题前,首先要引入一个东西:
\(\vec{a} \times \vec{b}\) 的结果不同于点乘,叉乘的结果还是一个向量,两个向量叉积的结果是垂直于这两个向量所在平面的一个向量,而其模长为两向量模长相乘再乘上这两个向量的夹角的正弦值。
即\(|\vec{a}\times \vec{b}| = |\vec{a}||\vec{b}|\sin<\vec{a},\vec{b}>\),其方向可以由右手定则确定。
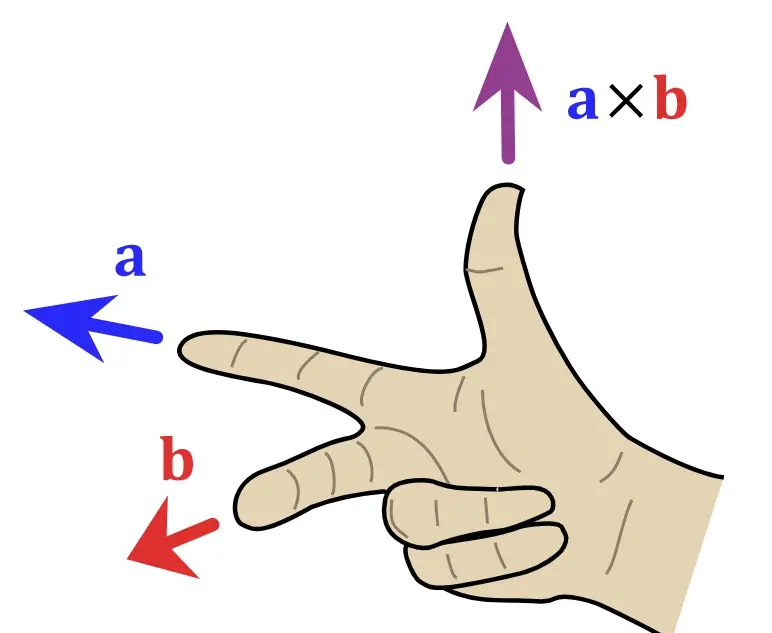
该叉积结果的模长的几何意义,其实就是将两向量的起点移到一起所形成的平行四边形的面积。
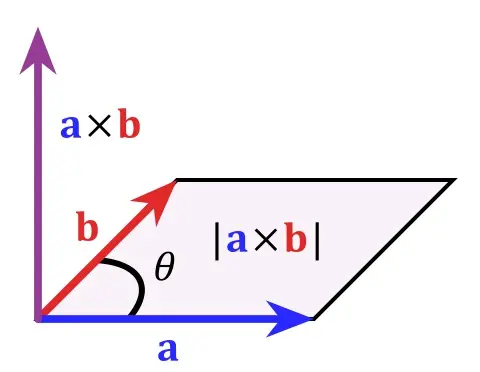
而两向量 \(\vec{a}(x1,y1,z1)\),\(\vec{b}(x2,y2,z2)\) 的叉乘结果 \(\vec{a} \times \vec{b}=(y1z2-z1y2,z1x2-x1z2,x1y2-y1x2)\)
现在回到本题,补全截面并建系得下图:

截面面积显然为\(|\overrightarrow{FG} \times \overrightarrow{FA_1}|\) ,而\(\overrightarrow{FG}(-4,8\lambda-4,0)\) ,\(\overrightarrow{FA_1}(0,4\lambda,1)\) ,得 \(\overrightarrow{FG} \times \overrightarrow{FA_1} = (8\lambda-4,4,-16\lambda)\) ,则\(\begin{aligned}|\overrightarrow{FG} \times \overrightarrow{FA_1}|^2 & = (8\lambda-4)^2 + 4^2 + (-16\lambda)^2 \\ & = 320\lambda ^ 2 - 64\lambda + 32 \\ & = 320(\lambda - \frac{1}{10}) ^ 2 + \frac{144}{5} \end{aligned}\)
在\(\lambda = \frac{1}{10}\) 时取得最小值 \(\frac{144}{5}\) ,则面积最小值为\(\frac{12\sqrt{5}}{5}\)
T19(附加第一题)
题面

解法
直接上结论,写不动了,具体不证了,在三个坐标轴上任选三点用向量证明即可。
点 \((i,j,k)\) 到平面 \(Ax + By + Cz + D = 0\) 的距离为\(\frac{|Ai + Bj + Ck + D|}{\sqrt{A^2 + B^2 + C^2}}\)
题中直接给出了平面的方程式,而\(|\overrightarrow{OP} - \overrightarrow{OA} - \overrightarrow{OB}|\) 的几何意义其实就是存在一点坐标为 \(\overrightarrow{OA} + \overrightarrow{OB}\) 的点到该平面的距离。
那么答案就是
\(\begin{aligned} \frac{1+2-1}{\sqrt{1^2+2^2+4^2}} & = \frac{2}{\sqrt{21}} \\ & = \frac{2\sqrt{21}}{21}\end{aligned}\) ,这里有一点需要注意的时等式右边的常数项要记得移过来,使得等式右边变为零。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号