Acwing 周赛88 题解
·A题
题目描述
给定一个整数\(x\)，请你找到严格大于\(x\)且各位数字均不相同的最小整数\(y\)。
\(1000 \le x \le 9000\)
做法分析
发现数据范围很小，那么我们可以直接从\(x+1\)进行枚举，同时使用一个 check 函数检查是否满足条件。
代码
#include <bits/stdc++.h>
using namespace std;
int x;
bool check(int a)
{
int num[10];//0-9每一个数字是否出现过
for(int i = 0; i < 10; i++)
num[i] = 0;//初始化全部没出现过
while(a > 0)
{
if(num[a % 10])
return 0;//个位数出现过，返回不成立
num[a % 10]++;
a /= 10;//往后缩一位
}
return 1;//坚持到了最后，说明符合条件
}
int main()
{
scanf("%d", &x);
for(int i = x + 1; ; i++)
{
if(check(i))//如果符合
{
printf("%d", i);
return 0;//输出并返回
}
}
return 0;
}
·B题
题目描述
给定一个平面。
平面中有 n 条与 x 轴平行的有向边，从上到下依次编号为 1 ~ n ，每条边都无限长，且两两不重合。
平面中有 m 条与 y 轴平行的有向边，从左到右依次编号为 1 ∼ m ，每条边都无限长，且两两不重合。
这些边一共有 n × m 个交点。
给定每条边的具体方向，请你判断这 n × m 个交点是否满足：从任意交点出发可以到达任意其它交点。
\(2 \le n,m \le 20\)
做法分析
首先先对样例1进行一个图的画，我们得到下图：
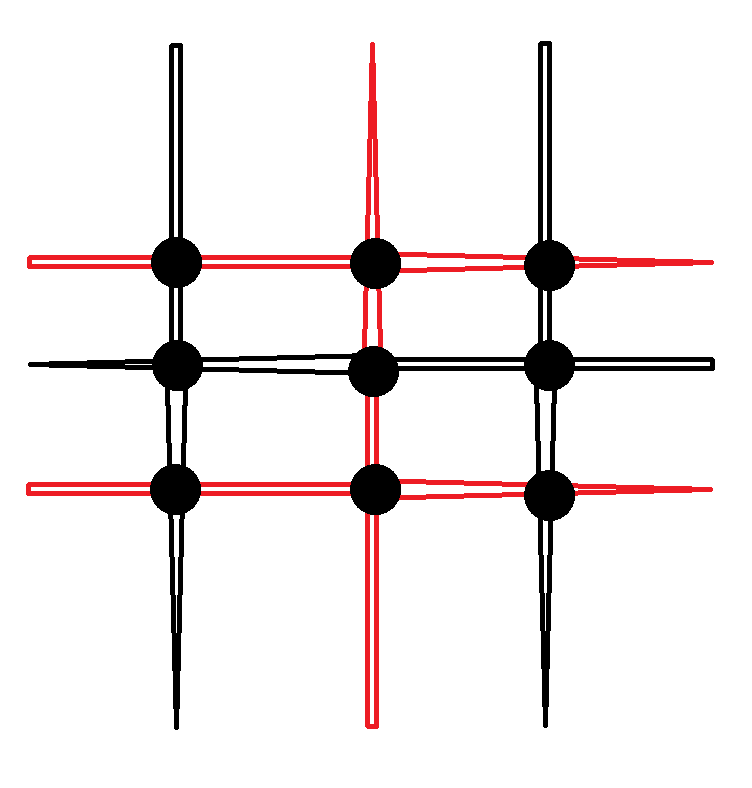
发现一点，其实最终我们需要的就只有围成的一个矩形。
先进行矩形的四个角的讨论，也就是先讲问题简化成只有两条竖线两条横线的情况。只有两种情况能够满足：四条线围成的矩形顺时针或逆时针连通，也就是下图两种情况：
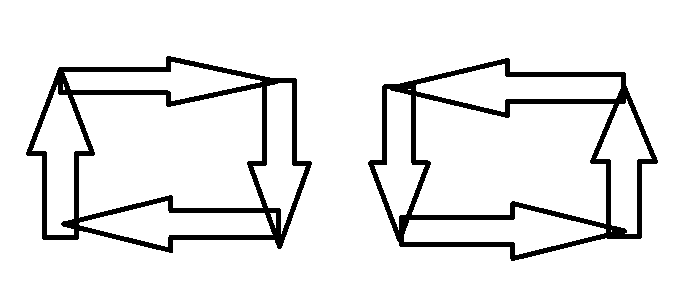
所以我们得到了答案成立的初步条件，即上面的两种情况。
然后发现这两种情况与答案满足是等价的：因为对于任意一个点，我们可以先沿着所在边的方向，到达最外圈，然后就可以通过这一圈到大任意一条边的入口，从而到达任意一点。
代码
#include <bits/stdc++.h>
#define MAXn 50
using namespace std;
int n, m;
char a[MAXn], b[MAXn];
int main()
{
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; i++)
cin >> a[i];
for(int i = 1; i <= m; i++)
cin >> b[i];
if(a[1] == '>' && a[n] == '<' && b[1] == '^' && b[m] == 'v')//顺时针
{
printf("YES\n");
return 0;
}
if(a[1] == '<' && a[n] == '>' && b[1] == 'v' && b[m] == '^')//逆时针
{
printf("YES\n");
return 0;
}
printf("NO\n");//都不符合输出NO
return 0;
}
·C题
题目描述
金明有 n 天假期，编号 1 ∼ n。
整个假期期间，他每天只可能有三种选择：
去健身房健身一整天。（前提是当天健身房开放）
去图书馆看书一整天。（前提是当天图书馆开放）
在家休息一整天。
用一个长度为 n 的整数数组 a1,a2,…,an 来表示这 n 天健身房与图书馆的开放情况，其中：
\(a_i\) 等于 0 表示第 i 天健身房关闭且图书馆关闭。
\(a_i\) 等于 1 表示第 i 天健身房关闭但图书馆开放。
\(a_i\) 等于 2 表示第 i 天健身房开放但图书馆关闭。
\(a_i\) 等于 3 表示第 i 天健身房开放且图书馆开放。
金明希望自己用来休息的天数尽可能少，但是，他一定不会连续两天（或更多天）去健身房健身，也一定不会连续两天（或更多天）去图书馆看书。
请你计算，金明用来休息的最少可能天数。
\(1 \le n \le 100,0 \le a_i \le 3\)
题目分析
一眼的状态机DP。
设f[i][j]表示第 i 天状态是 j 时（0 -- 休息，1 -- 去图书馆， 2 -- 去健身房），前 i 天出去的天数。
当第 i 天在家休息时，f[i][0]继承前一天的最大值即max(f[i - 1][0], f[i - 1][1], f[i - 1][2])。
当第 i 天去图书馆时，f[i][1]是前一天在家休息或去健身和钱两天去图书馆中的最大值再加 1 ，因为这一天出去了，即max(f[i - 1][0], f[i - 2][1], f[i - 1][2])。
当第 i 天去健身房时于去图书馆同理即max(f[i - 1][0], f[i - 1][1], f[i - 2][2])。
这里有一个问题，如果上一天图书馆或健身房不开，这一天的这个状态怎么办呢，我们不用管他，因为没有开放的话就不用更新答案，在下一次使用时就为 0 ，不影响结果
代码
#include <bits/stdc++.h>
using namespace std;
int n;
int a[100], f[100][3];//在家，图书馆，健身房
int main()
{
scanf("%d", &n);
for(int i = 1; i <= n; i++)
scanf("%d\n", &a[i]);
for(int i = 1; i <= n; i++)
{
f[i][0] = max(max(f[i - 1][0], f[i - 1][1]), f[i - 1][2]);
if(a[i] == 1) f[i][1] = max(max(f[i - 1][0], f[i - 2][1]), f[i - 1][2]) + 1;
if(a[i] == 2) f[i][2] = max(max(f[i - 1][0], f[i - 2][2]), f[i - 1][1]) + 1；
if(a[i] == 3)
{
f[i][1] = max(max(f[i - 1][0], f[i - 2][1]), f[i - 1][2]) + 1;
f[i][2] = max(max(f[i - 1][0], f[i - 2][2]), f[i - 1][1]) + 1;
}
}
printf("%d", n - max(max(f[n][0], f[n][1]), f[n][2]));
return 0;
}
