贝叶斯决策

周志华《机器学习》笔记

1.贝叶斯决策简介

贝叶斯决策是基于所有相关概率已知情况下，结合误判损失来选择最优的类别标记的一种决策方法。
假设有N种可能的标记， $λ_{i j}$ 是将一个真实标记为 $c_{i}$ 的样本误判为类别 $c_{j}$ 所产生的损失。

条件风险

R (c_{i} | x) = \sum_{j = 1}^{N} λ_{i j} P (c_{j} | x)

因为知道后验概率

P (c_{i} | x)

，所以给定一个样本，能够得到它被分为每个类别的概率。把所有误分的概率乘以损失，就得到了误分的代价，把每个样本误分为其他的类别的代价相加，就是这个条件风险。

贝叶斯准则

为最小化总体风险，只需在每个样本上选择那个能使条件风险最小的类别标记。
使用0\1损失函数作为误分类的风险，也就是说当分类正确时，损失为0，否则损失为1. 这时候条件风险的表达式将变得很简单，

R (c_{i} | x) = \sum_{j = 1 ， i \neq j}^{N} P (c_{j} | x) = 1 - P (c_{i} | x)

最小化分类错误率的贝叶斯最优化分类器

h^{*} (x) = \underset{c \subset γ}{a r g m a x} P (c | x)

即对每一个样本x，选择能够使后验概率

P (c | x)

的最大的类别标记。

2.如何获得后验概率？

基于有限的样本训练集尽可能地估算出后验概率 $P (c | x)$ 。这里使用生成模型，先对联合概率分布 $P (c, x)$ 建模，然后再求边缘分布，即 $P (c | x)$ 。即

P (c | x) = \frac{P (c, x)}{P (x)}

使用贝叶斯定理

P (c | x) = \frac{P (x | c) P (c)}{P (x)}

其中

P (c)

是先验概率，类条件概率

P (x | c)

P (x)

为归一化因子。
先验概率可以通过各样本的类别出现的频率估算。
类条件概率

P (x | c)

使用极大似然估计求。

3.极大似然估计求类条件概率 $P (x | c)$

基本思路：假定样本具有某种确定的概率分布形式，再基于样本对概率分布的参数进行估计。
按照类别把数据分成不同的子集，假设每个子集中的样本都是独立同分布的，写出似然函数:

P (D_{c} | θ_{c}) = \prod P (x | θ_{c})

取对数求得对数似然函数：

L (θ_{c}) = \sum l o g P (x | θ_{c})

然后求

θ_{c}

一阶，二阶导数，令一阶导数值为0，若二阶导数小于0，则函数在这个

θ

出取得最大值。

4.朴素贝叶斯分类器

为什么叫朴素贝叶斯呢？因为类条件概率很难从有限的样本中直接估计得到，所以引入了一个属性条件独立性假设，对已知的类别，假设所有属性都是相互独立的。但是实际中，这些属性之间并不总是独立的，因此说他朴素(Naive)。
于是有 $P (c | x) = \frac{P (x | c) P (c)}{P (x)} = \frac{P (c)}{P (x)} \prod_{i = 1}^{d} P (x_{i} | c)$ , d为属性的个数, $x_{i}$ 为第i个属性上的取值。
朴素贝叶斯分类器的表达式：

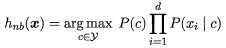
比如西瓜数据集

编号,色泽,根蒂,敲声,纹理,脐部,触感,密度,含糖率,好瓜
1,青绿,蜷缩,浊响,清晰,凹陷,硬滑,0.697,0.46,是
2,乌黑,蜷缩,沉闷,清晰,凹陷,硬滑,0.774,0.376,是
3,乌黑,蜷缩,浊响,清晰,凹陷,硬滑,0.634,0.264,是
4,青绿,蜷缩,沉闷,清晰,凹陷,硬滑,0.608,0.318,是
5,浅白,蜷缩,浊响,清晰,凹陷,硬滑,0.556,0.215,是
6,青绿,稍蜷,浊响,清晰,稍凹,软粘,0.403,0.237,是
7,乌黑,稍蜷,浊响,稍糊,稍凹,软粘,0.481,0.149,是
8,乌黑,稍蜷,浊响,清晰,稍凹,硬滑,0.437,0.211,是
9,乌黑,稍蜷,沉闷,稍糊,稍凹,硬滑,0.666,0.091,否
10,青绿,硬挺,清脆,清晰,平坦,软粘,0.243,0.267,否
11,浅白,硬挺,清脆,模糊,平坦,硬滑,0.245,0.057,否
12,浅白,蜷缩,浊响,模糊,平坦,软粘,0.343,0.099,否
13,青绿,稍蜷,浊响,稍糊,凹陷,硬滑,0.639,0.161,否
14,浅白,稍蜷,沉闷,稍糊,凹陷,硬滑,0.657,0.198,否
15,乌黑,稍蜷,浊响,清晰,稍凹,软粘,0.36,0.37,否
16,浅白,蜷缩,浊响,模糊,平坦,硬滑,0.593,0.042,否
17,青绿,蜷缩,沉闷,稍糊,稍凹,硬滑,0.719,0.103,否

这里就假设属性色泽,根蒂,敲声,纹理,脐部,触感,密度,含糖率之间是相互独立的。

5. 朴素贝叶斯分类的例子

根据这些属性先把数据划分为一个个子集，然后为每个属性的取值估计条件概率 $P (x_{i} | c)$ 。
变量是有离散和连续之分的，对于离散型的变量，直接使用频率估计概率；
对于连续变量，常常假设其服从高斯分布，分别求第c类样本在第i个属相上取值的均值和方差 $μ_{c, i}$ , $σ_{c, i}^{2}$ , 然后使用求类条件概率：

p (x_{i} | c) = \frac{1}{\sqrt{2 π} σ_{c, i}} e x p (- \frac{(x_{i} - μ_{c, i})^{2}}{2 σ_{c, i}^{2}})

看周老师书上的一个例子去理解：

6.平滑

如果某个属性在训练集中没有出现过，那么其列条件概率为0，使用朴素贝叶斯估计时由于其中一项为0，导致最终结果为0。
使用拉普拉斯修正对其做平滑。
具体的做法是

\hat{P} = \frac{| D_{c} | + 1}{| D | + N}

\hat{P} (x_{i} | c) = \frac{| D_{c, x_{i} |} | + 1}{| D_{c} | + N_{i}}

N表示类别数，

N_{i}

表示第

i

个属性可能的取值数目。

周志华《机器学习》

posted @ 2018-09-02 15:02 Siucaan 阅读(950) 评论(0) 编辑收藏举报

Siucaan